Laboratorium z fizyki

Temat: Wyznaczanie temperatury Curie dla ferrytu.

1. Temat ćwiczenia.

Wyznaczanie temperatury Curie dla ferrytów.

2. Wprowadzenie.

Ferrytami nazywamy związki chemiczne określone wzorem:

gdzie Me jest metalem dwuwartościowym, np.: mangan, magnez, cynk, nikiel, miedź,

a "m" i "n" są liczbami całkowitymi.

Podział ferrytów:

-ferrospinele:

-ferryty związków itru i lantanowców:

-ortoferryty:

-heksaferryty (Me oznacza bar , ołów):

-związki tlenków baru i żelaza:

-magnetyt:

Cechą charakterystyczną ferrytów jest ich duża oporność właściwa, co pozwala na budowę rdzeni magnetycznych o małych stratach związanych z prądami wirowymi.

Własności elektryczne większości ferrytów pozwalają na zakwalifikowanie ich do grupy półprzewodników. Własności magnetyczne zależą od momentów magnetycz-nych jonów i ich wzajemnego oddziaływania. Rozróżniamy trzy materiałów o włas-

nościach magnetycznych:

-ferromagnetyki,

poniżej temperatury Curie momenty magnetyczne ustawiają się równolegle do siebie,

a zwroty są zgodne. Powyżej tej temperatury intensywne ruchy cieplne zaburzają to uporządkowanie i ferromagnetyk przechodzi w stan paramagnetyczny.

Prawo Curie dotyczące zależności podatności magnetycznej ferromagnetyków od temperatury w zakresie słabych pól:

N - koncentracja cząstek

-antyferromagnetyki,

momenty magnetyczne ustawiają się antyrównolegle, wykazują własności magnetyczne tylko w obecności zewnętrznego pola magnetycznego. Powyżej temperatury Neela uporządkowana struktura ulega zaburzeniu i materiał staje się parametrykiem (antyfer-romagnetyczny punkt Curie).

-ferrimagnetyki (antyferromagnetyki nieskompensowane)

momenty magnetyczne sąsiednch atomów ustawione są antyrównolegle. W strukturze występują w tzw. podsieci o nieskompensowanym wypadkowym momencie magne-tycznym. W zewnętrznym polu magnetycznym ferrimagnetyki zachowują się podobnie jak ferromagnetyki. Powyżej pewnej charakteystycznej temperatury, zwanej tempera- turą Neela, ferrimagnetik staje się paramagnetykiem. W tej temperaturze zachodzi zmiana struktury i zmieniają się skokowo również inne własności, np.: ciepło molowe, współczynnik rozszerzalności cieplnej.

Na rurze ze szkła kwarcowego nawinięto transormator.Wewnątrz umieszcza się badany,cylindryczny rdzeń ferrytowy. W kontakcie z rdzeniem znajduje się złącze termopary, której drugi koniec posiada temperaturę otoczenia.Prąd płynący w uzwojeniu pierwotnym transformatora powoduje wydzielenie się cieopła i ogrzewanierdzenia ferrytowego. Ferryt otoczony jest płaszczem izolacyjnym.

Po osiągnięciu temperatury Cirie przez rdzeń następuje gwałtowny spadek przenikalności magnetycznej rdzenia ferrtyowego i natężenie prądu w uzwojeniu wtórnym gwałtownie spada. Ze względu na bezwładność cieplną układu oraz gradient temperatury w rdzeniu spadek prądu odbiega od przewidywań teoretycznych. Temperatura Curie odpowiada spadkowi natężenia prądu do połowy wartości maksymalnej.

3. Przebieg ćwiczenia:

a) łączenie obwodu,

b) kontrola prawidłowości ustawienia mierników,

c) ustalenie napięcia zasilającego na ok. 52 V,

d) notowanie wskazań mierników w odstępach czasowych 1 min,

e) rysowanie wykresów:

- cechowania termoogniwa

- zależności natężenia prądu od temperatury rdzenia ferrtyowego,

f) określenie temperatury Curie i ocenienie błędów pomiarowych.

4. Schemat obwodu do wyznaczania temperatury Curie ferrytów.

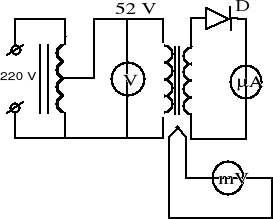
Dokonano dwadziścia osiem pomiarów napięcia i natężenia prądu w uzwojeniu wtórnym wyżej narysowanego układu.

Zakres miliwltomireza wynosił Z = 10 mV, natomiast klasa dokładności kd = 1.

Całkowite wychylenie miliwoltomierza wynosi 100 mV, stąd wniosek, że stała podziałki wynosi 0.1. Dlatego wskazania miliwoltomierza mnozymy razy syałą podziałki.

Zakres, klasa dokładności, oraz całkowite wychylenie mikroamperomierza są takie same jak przy miliwoltomierzu, więc działania są analogiczne.

Poprawne winiki wpisane zostały do tabeli pomiarowej

Tabela pomiarowa

Lp.	t [s]	i []	[mV]		Lp.	t [s]	i []	[mV]
1	0	6.5	0.6		15	800	3.45	4.35
2	60	6.5	0.8		16	820	3.05	4.5
3	120	6.5	1.1		17	840	2.8	4.55
4	180	6.5	1.8		18	860	2.55	4.6
5	240	6.5	2.1		19	880	2.35	4.7
6	300	6.7	2.4		20	900	2.2	4.7
7	360	6.7	2.7		21	920	2.05	4.7
8	420	6.9	3.0		22	940	1.9	4.8
9	480	6.75	3.3		23	960	1.75	4.8
10	540	6.65	3.5		24	980	1.65	4.9
11	600	6.45	3.75		25	1000	1.55	4.9
12	660	6.0	3.9		26	1020	1.45	5.0
13	720	5.0	4.2		27	1040	1.35	5.0
14	780	3.8	4.3		28	1062	1.3	5.1

Błędy bezwzględne pomiarów miliwoltomierzem i mikroamperomierzem są takie same i wynoszą:

I = 0.1 [ A ]

= 0.1 [ mV ]

Błąd względny pomiarów wyraża się wzorem

i wynosi dla każdego pomiaru:

Tabele błędów względnych

Lp.	i []	[mV]		Lp.	i []	[mV]
1	0.0154	0.167		15	0.0290	0.023
2	0.0154	0.125		16	0.0328	0.023
3	0.0154	0.091		17	0.0357	0.022
4	0.0154	0.056		18	0.0392	0.022
5	0.0154	0.048		19	0.0426	0.022
6	0.0149	0.048		20	0.0455	0.021
7	0.0149	0.042		21	0.0488	0.021
8	0.0145	0.037		22	0.0526	0.021
9	0.0148	0.033		23	0.0571	0.021
10	0.0150	0.030		24	0.0606	0.021
11	0.0155	0.029		25	0.0645	0.020
12	0.0167	0.027		26	0.0690	0.020
13	0.0200	0.026		27	0.0741	0.020
14	0.0263	0.024		28	0.0769	0.020

Tabela cechowania termoogniwa:

[ mV ]	T [ K ]	[ mV ]	T [ K ]
3.46	373	6.36	443
3.87	383	6.77	453
4.29	393	7.19	463
4.70	403	7.60	473
5.12	413	8.01	483
5.53	423	8.43	493
5.94	433

Wykres cechowania termoogniwa

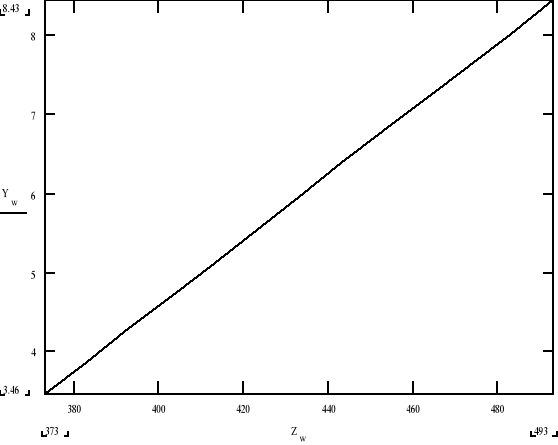
Z powyższego wykresu odczytujemy wartość temperatury wyrażonej w K . Jak widać dokonane pomiary nie mieszczą się w pełni w zakresie cechowania i musieliśmy je odrzucić. Otrzymaną temperaturą wykorzystujemy do zależność natężenia prądu w uzwojeniu wtórnym transformatora od temperatury, co umożliwia nam określenie temperatury Curie dla ferrytu

Błąd temperayury jest proporjonalny do błędu napięcia, względem którego został wyznaczony i wynosi dla:

[mV]	T [K]	T [K]	[mV]	T[K]	T [K]
3.50	374.1	3.3	4.7	403.2	2.6
3.75	380.2	3.1	4.7	403.2	2.6
3.90	383.8	3.0	4.8	405.5	2.6
4.20	391.1	2.8	4.8	405.5	2.6
4.30	393.5	2.8	4.9	407.8	2.5
4.35	394.6	2.8	4.9	407.8	2.5
4.50	398.3	2.7	5.0	410.2	2.5
4.55	399.4	2.7	5.0	410.2	2.5
4.60	400.8	2.7	5.1	412.6	2.5
4.70	403.2	2.6	Błąd średni		2.7

Zależność natężenia prądu w uzwojeniu wtórnym transformatora od temperatury

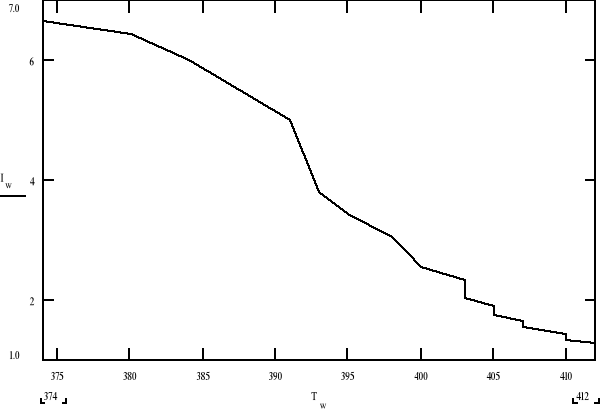
Określenie temperatury Curie dla ferrytu

Temperatura Curie odpowiada spadkowi natężenia prądu do połowy wartości maksymalnej.

Maksymalny prąd wynosił: 6.65 A

Połowa maksymalnego prądu wynosi: 3.33 A

Dla takiej wartości połowy prądu tmperatura wynosi 395,89 K i jest to temperatura Curie dla ferrytu.

Błędy pomiaru obliczamy za pomocą graficznej analizy błędów i wynoszą:

T = 2 błąd maksymalny I = 2 błąd maksymalny

T = 2 3,3 [K] I = 0,98 [A]

T= 6,6 [K] I= 0.98 [A]

Ostateczna temperatura Curie dla ferrytu wynosi: 395,9 6,6 [K]

Wnioski

Aby móc określić temperaturę Curie dla ferrytu należy mieć dane by narysować wykres cechowania termoogniwa aby przejść z wartości napięcia zmierzonych podczas ćwiczenia na odpowiednie wartości temperatury wyrażonej w K.

Aby otrzymać bardzo dokładny wykres zależności natężenia prądu w uzwojeniu wtórnym transformatora od temperatury należałoby wykonywać odczyty w bardzo krótkich okresach czasu. Nasze pomiary były robione najpierw co 1 minutę, potem co 20 sekund. W celu oszacowania błędu przyjęto metodę graficznej analizy błędów.

---