Politechnika Śląska w Gliwicach
Podstawy Konstrukcji Maszyn
Projekt manipulatora robota
Projekt opracował:
Gawlik Marek
Wydział: Mechaniczny Technologiczny
Kierunek: Automatyka i Robotyka
Grupa: I
Rok studiów: III
Semestr V
Rok akademicki: 1999/2000
TEMAT PROJEKTU
Zaprojektować manipulator robota obsługujący dwie obrabiarki tworzące wspólne gniazdo zrobotyzowane. Przedmiotem manipulacji jest walec o średnicy d i wysokości h.
2. Założenia wstępne
2.1 Dane sytuacyjne:
Obrabiarki mogą być w różny sposób względem siebie usytuowane.
Obrabiarka pierwsza posiada uchwyt samocentrujący dolny na wysokości h1 od poziomu.
Obrabiarka druga posiada uchwyt samocentrujący górny na wysokości h2 od poziomu.
2.2 Kryteria projektowe
Minimalna masa manipulatora.
Minimalna długość ruchu jałowego.
Prostota działania i wykonania manipulatora.
Modułowość budowy manipulatora.
Błąd pozycjonowania 0,2÷0,4 cm.
Maksymalny stopień wykorzystania elementów znormalizowanych i stypizowanych.
Trwałość ( łożyskowa ) układów przegubowych powyżej 20.000 godzin pracy.
2.3 Dane ilościowe
- wysokość manipulowanego walca:
h = 180 mm,
- średnica manipulowanego walca:
d = 100 mm,
- wysokość uchwytu samocentrującego obrabiarki pierwszej:
h1 = 1200 mm,
- wysokość uchwytu samocentrującego obrabiarki pierwszej:
h2 = 1000 mm,
- średnica obszaru roboczego:
D = 4 m ,
- masa chwytaka:
mCH = 6 kg.
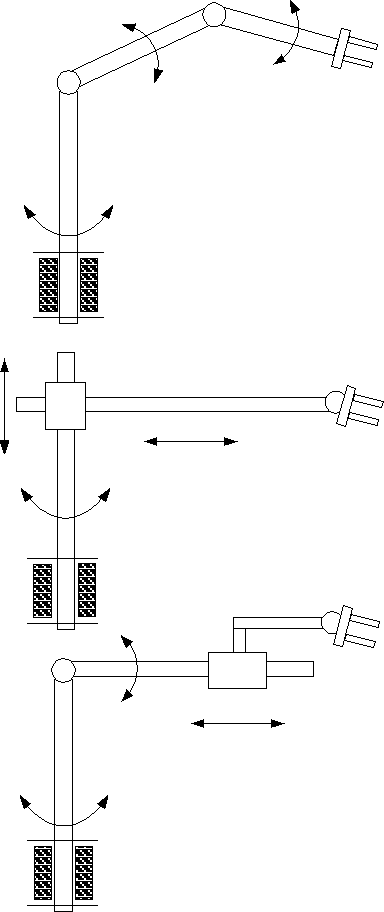
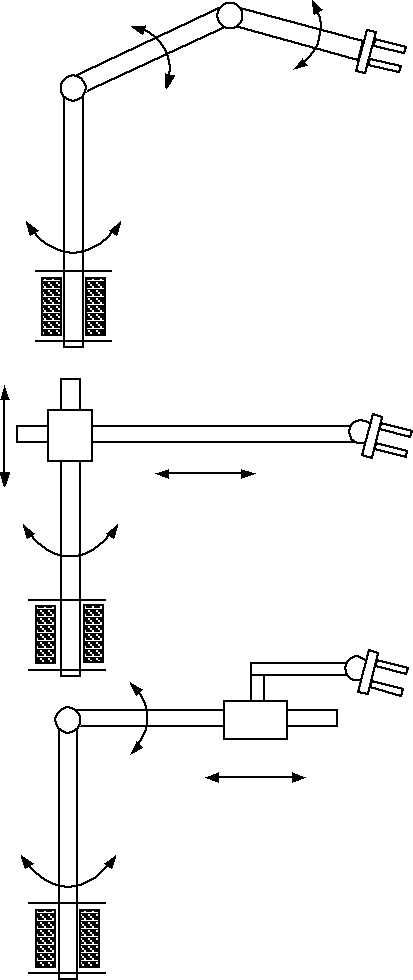
3. Warianty manipulatora
Optymalizacja
W wyborze optymalnego wariantu do realizacji posłużę się następującą tabelą:
X |
K1 |
K2 |
K3 |
K4 |
K5 |
K6 |
K7 |
ΣKi |
W1 |
W2 |
W3 |
Wi |
K1 |
X |
0,5 |
1 |
1 |
0,5 |
0,5 |
1 |
4,5 |
4 |
3 |
3 |
5 |
K2 |
0,5 |
X |
1 |
1 |
0,5 |
0,5 |
1 |
4,5 |
4 |
4 |
4 |
5 |
K3 |
0 |
0 |
X |
0,5 |
0 |
0,5 |
0,5 |
1,5 |
4 |
4 |
3 |
5 |
K4 |
0 |
0 |
0,5 |
X |
0 |
0,5 |
0 |
1 |
4 |
3 |
3 |
5 |
K5 |
0,5 |
0,5 |
1 |
1 |
X |
1 |
1 |
5 |
4 |
3 |
3 |
5 |
K6 |
0,5 |
0,5 |
0,5 |
0,5 |
0 |
X |
0,5 |
2,5 |
5 |
4 |
5 |
5 |
K7 |
0 |
0 |
0,5 |
1 |
0 |
0,5 |
X |
2 |
4 |
4 |
4 |
5 |
|
|
|
|
|
|
|
|
|
86,5 |
73,5 |
74,5 |
105 |
|
|
|
|
|
|
|
|
|
0,824 |
0,7 |
0,71 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Skala 3-5 |
|
|
|
|
|
|
Na podstawie tabeli i własnych przemyśleń dochodzę do wniosku, że najlepszym rozwiązaniem jest wariant pierwszy.
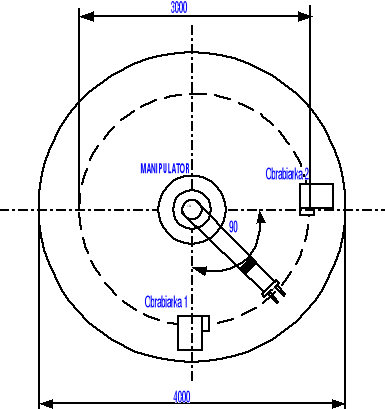
Ustawienie obrabiarek w gnieździe produkcyjnym
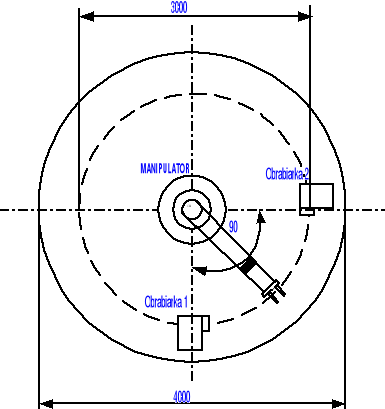
Obliczenia
6.1 Obliczenie maksymalnego kąta wychylenia ramienia
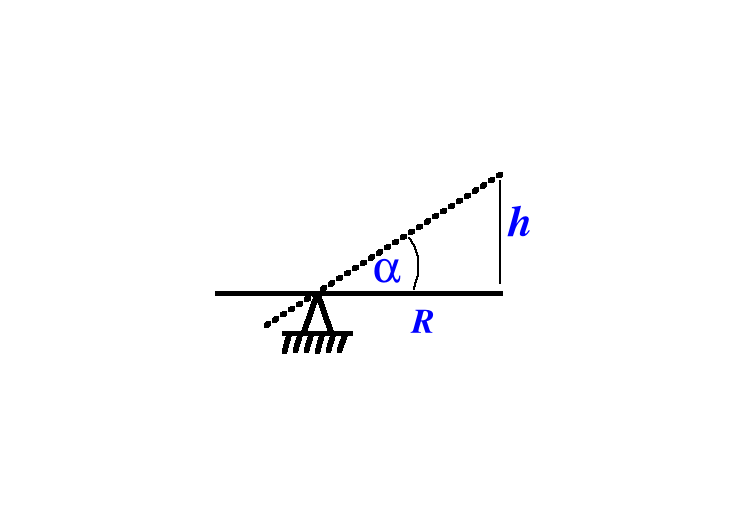
Dane:
h = 0.1 [m]
R = 2.0 [m]
Szukane:
α = ?
![]()
Do dalszych obliczeń przyjmuję α = 3°.
6.1b Obliczenie skoku siłownika

Dane:
AO=BO=CO=DO=0.5 m.
α = 3°
Szukane:
BA,DA=?
![]()
= 90° - α = 87°
![]()
= (180° - ![]()
) / 2 = (180° - 87°) / 2 = 46,5°
z trójkąta OAB wynika:
![]()
EA = 0.5*cos 46,5°=0.344m.
Wysięg minimalny siłownika wynosi:
Lmin=2*EA=2*0.344=0.688m.
z trójkąta OAD wynika:

![]()
= 90° + α = 93°
![]()
= (180° - ![]()
) / 2 = (180° - 93°) = 43,5°
![]()
FA = OA* cos 43,5° = 0.362m.
Wysięg maksymalny siłownika wynosi:
Lmax = 2*FA = 0.725m.
Skok siłownika jest zatem równy:
S = Lmax - Lmin
S = 0.725 - 0.688 = 0.037m = 37 mm
6.3 Obliczenia reakcji podpory oraz siły działania siłownika.
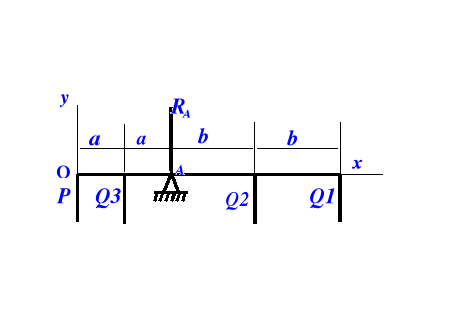
Dane:
a = 0.25 m.
b = 4*a = 1m.
Szukane:
Q1,Q2,Q3,RA,P=?
Określenie wielkości sił działających ramię manipulatora
siła Q1
![]()
Składa się z dwóch ciężarów, ciężaru chwytaka oraz elementu obrabianego![]()
mch - masa chwytaka,
mp - masa przedmiotu,
g - przyśpieszenie ziemskie.
Masa przedmiotu jest nieznana. Wyznaczam ją z warunków geometrycznych. Półfabrykat wykonany jest ze stali St5 o gęstości ρ = 7.89 [g/cm3] = 7860 [kg/m3].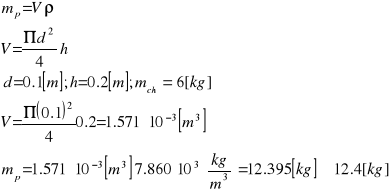
siła Q2
Zakładam, że ramię będzie wykonane z ceownika C200 PN—71/H—93451, którego masa wynosi 25.3 [kg/m].
Masa ramienia wynosi więc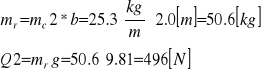
siła Q3
Siła Q3 równa jest iloczynowi masy ceownika na długości 2a i przyśpieszenia ziemskiego.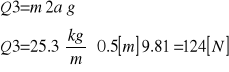
Równania równowagi
a) na oś y
Ra - P - Q1 - Q2 - Q3 = 0
b) równanie momentów względem punktu A![]()
Z równania (b) wyznaczamy reakcję podpory: 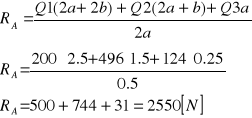
Z równania (a) wyznaczam siłę siłownika: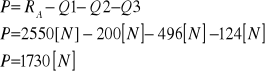
Dobór siłownika
Na podstawie wyżej przeprowadzonych obliczeń dobrałem siłownik firmy Mannesman Rexroth o oznaczeniu CD/H1/MP5/40/22.
6.4 Obliczenia wytrzymałościowe ramienia
Obliczanie maksymalnego momentu gnącego
Maksymalny moment gnący obliczam stosując metodę Clebscha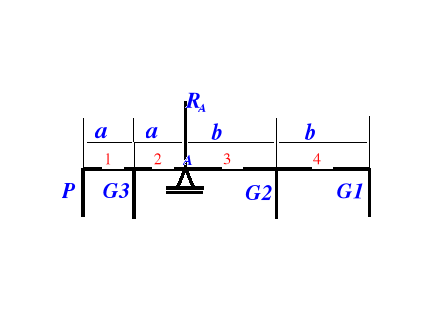
Dane:![]()
Q1=200 [N] P=1730 [N]
Q2=496 [N] a=0.25 m
Q3=124 [N] b=1.0 m
RA=2550 [N]
Równanie momentów gnących od strony lewej:![]()
Równanie momentów wstawiamy do równania różniczkowego osi ugiętej, a następnie dwukrotnie całkujemy:
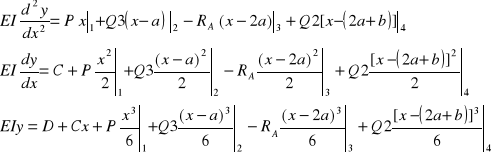
Warunki brzegowe:
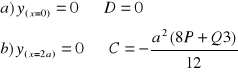
Ostatecznie więc równania przyjmują postać:
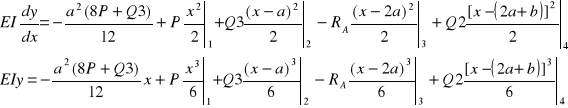
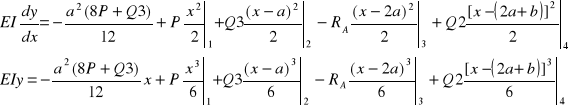
Po wstawieniu danych liczbowych otrzymujemy:
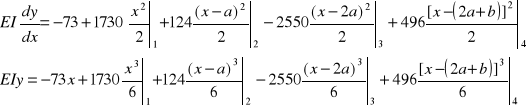
Ugięcie na końcu belki
Liczymy ugięcie w punkcie x=2a+2b=2,5 m.
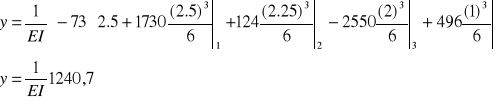
Korzystając z norm odczytujemy dane dla ceownika C200 PN:
Ix =1910 [cm4]=1910*10 -8[m4],
Iy =148 [cm4]=148*10 -8[m4].
oraz
E=2*105[Mpa]=2*1011[Pa].
Ugięcie jest zatem równe:
yx =3.25*10-4 [m],
yy =4.15*10-3 [m].
Wartości te spełniają założenia konstrukcyjne odnośnie dokładności pozycjonowania.
Maksymalny moment gnący w belce
Liczymy momenty gnące w belce korzystając z napisanego już wyżej równania momentów gnących od strony lewej:
![]()
Wstawiając wartości x dla poszczególnych przedziałów otrzymujemy następujące wartości momentów gnących na końcach przedziałów:
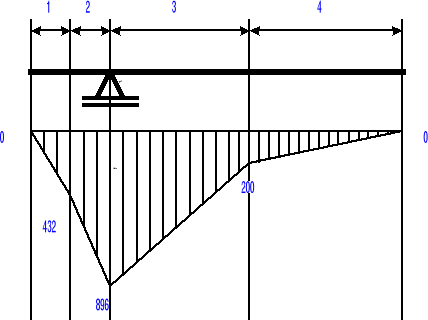
Mg (x=0) = 0 [Nm],
Mg (x=0.25) = -432.5 [Nm],
Mg (x=0.5) = -896 [Nm],
Mg (x=1.5) = -200 [Nm],
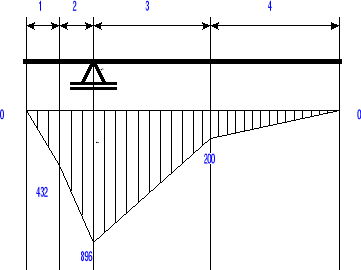
Mg (x=2.5) = 0 [Nm].
Na postawie otrzymanych danych tworzymy wykres momentów gnących.
Z wykresu widać, iż maksymalny moment znajduje się na końcu drugiego przedziału. Wartość momentu w tym punkcie wynosi Mg max = -896 [Nm].
Sprawdzenie warunku wytrzymałościowego
Warunek wytrzymałościowy ma następującą postać:
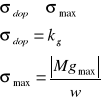
Dla stali kg=50*106
![]()
Wskaźniki wytrzymałości na zginanie dla ceownika C200 PN mają wartości:
wx=191 [cm3]=191*10-3 [m3],
wy=27 [cm3]=27*10-3 [m3].
Otrzymujemy więc:

Jak widać naprężenia w obu płaszczyznach są wyraźnie mniejsze od naprężeń dopuszczalnych, a więc warunek wytrzymałościowy jest spełniony.
6.5 Obliczenia dotyczące słupa oraz siłownika obrotowego ![]()
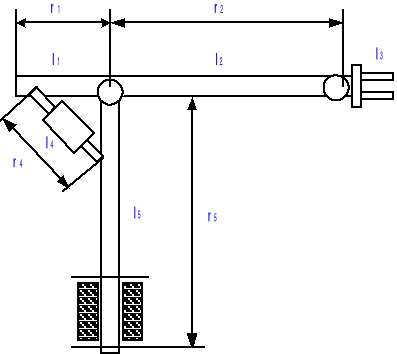
Wyznaczenie momentu obrotowego siłownika obrotowego
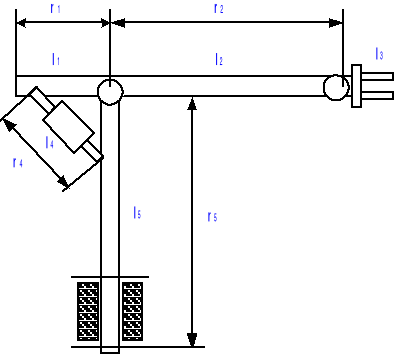
Zakładam, że słup będzie wykonany z rury stalowej bez szwu precyzyjnej według PN-91 H-74240 o średnicy zewnętrznej D=200 mm i grubości ścianki g=20 mm. oraz masie 88.8 kg/m.
Dane:
D=200 mm = 0.2 m. r1=0.5 m
d=160 mm = 0.16 m. r2=2.0 m
m1=12.65 kg r3=1.1 m
m2=50.6 kg r4=0.707 m
m3=20.4 kg
m4=2.0 kg ![]()
m5=97,68 kg
![]()
Szukane:
M=?
Moment obrotowy wyraża się następującym wzorem:
![]()
gdzie:
![]()
- suma momentów bezwładności od poszczególnych części robota,
- przyśpieszenie obrotowe.
Momenty bezwładności:
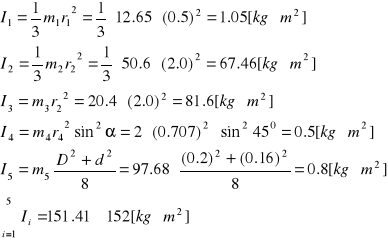
Moment obrotowy jest zatem równy:
![]()
Z katalogu MANNESMANN REXROTH dobrałem siłownik obrotowy o oznaczeniu RE 91180/04.93 A10FSM rozmiar 23 o maksymalnym momencie obrotowym 80 [Nm].
Weryfikacja słupa
Wymiary słupa zweryfikowałem obliczając go na wyboczenie.

Dane:
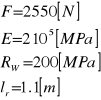
Przy obliczeniach na wyboczenie korzystam ze wzoru Eulera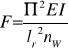
gdzie:
nW= (1.3 ÷ 4) - współczynnik bezpieczeństwa ze względu na wyboczenie
Do obliczeń przyjmuję nW = 4.
Ze wzoru Eulera wyznaczam moment bezwładności I.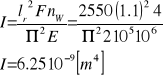
Średnicę zewnętrzną słupa wynosi dz = 200 [mm], natomiast średnica wewnętrzna jest równa dw = 160 [mm]. Średnica wyrażana przez grubość ścianki g wygląda więc następująco: dz = 10g, dw = 8g, czyli g = 20 [mm].
Obliczam moment bezwładności I![]()
Porównując moment bezwładności wyliczony ze wzoru Eulera oraz moment bezwładności wyrażony przez grubość ścianki otrzymuję: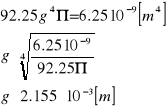
Sprawdzam warunek na smukłość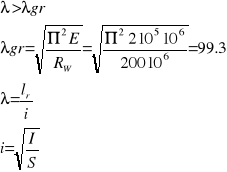
gdzie:
i - promień bezwładności
S - pole przekroju
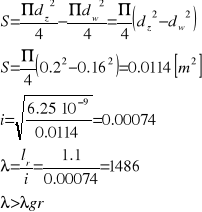
Warunek wytrzymałościowy został więc spełniony
6.6 Łożyskowanie
Na słupie osadzone będą dwa łożyska toczne. Łożysko górne przenosić będzie tylko obciążenie poprzeczne. Łożysko dolne przenosić będzie całe obciążenie wzdłużne oraz część obciążenia poprzecznego.
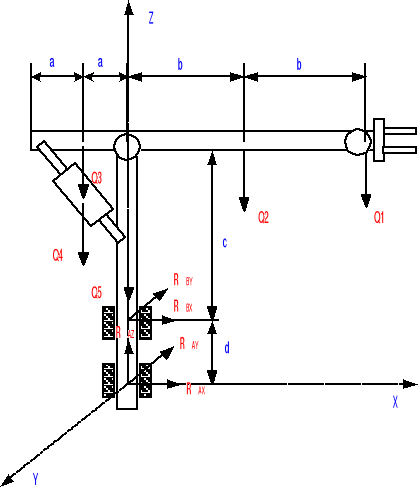
Ponieważ prędkości i przyśpieszenia obrotowe robota są małe, to prędkości i przyśpieszenia liniowe poszczególnych części (mas) robota będą również niewielkie dlatego pomijamy siły bezwładności przez nie wywołane, gdyż ich wpływ jest znikomy.
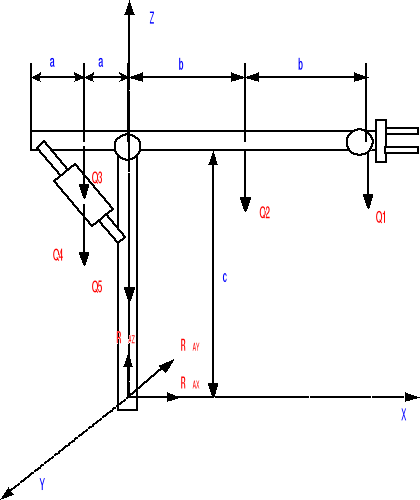
Dane:
Q1=200 [N] a=0.25 m
Q2=496 [N] b=1.0 m.
Q3=124 [N] c=0.7 m
Q4=20 [N] d=0.2 m.
Q5=958 [N]
Szukane:
RAX, RAY, RAZ, RBX, RBY=?
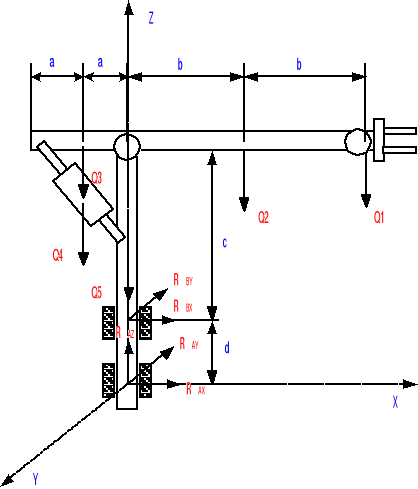
Szukane wartości znajduje korzystając z równań równowagi dla układu przestrzennego.
Równania równowagi:
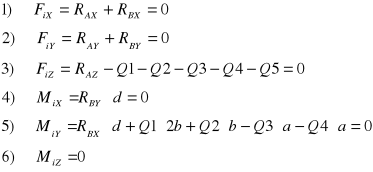
Po przekształceniach otrzymujemy:
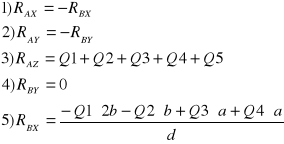
Ostatecznie:
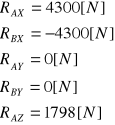
Dobór łożysk na słupie
Dane:
d=200 mm
n=2.5[obr/min]
trwałość łożyskowa = 20000 godzi pracy
a) łożysko górne - łożysko kulkowe
Zakładam, że łożyskiem górnym będzie łożysko kulkowe dla którego obciążenie statyczne równoważne wyraża się wzorem
P = X*Fr+Y*Fa
gdzie: Fr = RB=RBX,
Fa=0,
X=1.
Po podstawieniu otrzymujemy:
P = RBX =4300 [N]
Nośność spoczynkowa wyraża się wzorem:![]()
gdzie:
SO - współczynnik zabezpieczający łożysko przed zbyt dużym odkształceniem trwałym;
SO = 3.5 dla łożysk wałeczkowych
SO = 2 dla łożysk kulkowych.
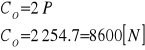
Dobieram łożysko kulkowe 61840 wg PN-85 M-86100 dla którego CO = 72500 [N], C = 73400 [N].
Sprawdzam, czy łożysko wytrzyma założone 20000 [h]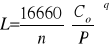
q =3 - dla łożysk kulkowych 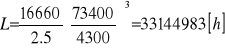
Trwałość łożyska jest wielokrotnie większa od wymaganej.
b) łożysko dolne
Zakładam, że łożyskiem dolnym będzie łożysko baryłkowe dla którego obciążenie równoważne statyczne obliczam ze wzoru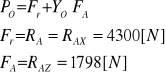
YO - współczynnik obciążeń statycznych; przyjmuję YO = 3.3
Po podstawieniu otrzymuje
![]()
Obliczam nośność statyczną łożyska ze wzoru
![]()
SO = 3.5 dla łożysk wałeczkowych
![]()
Dobieram łożysko baryłkowe 23936C / W33, dla którego CO = 73000 [N]; C = 431000 [N].
Sprawdzam czy łożysko wytrzyma założone 20000 [h].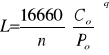
q = 10/3 dla łożysk wałeczkowych 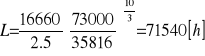
Stwierdzam, że trwałość łożyska jest wielokrotnie przekroczona.
6.7 Obliczenia śrub fundamentowych
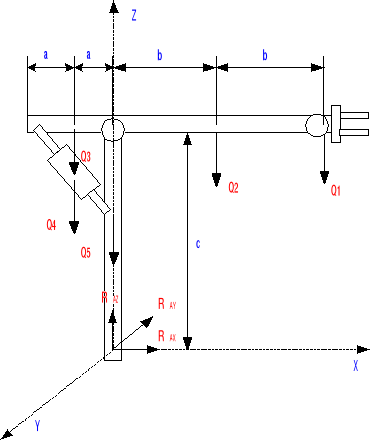
Pomijam siły bezwładności gdyż ich wpływ jest znikomy.
Dane:
Q1=200 [N] a=0.25 m
Q2=496 [N] b=1.0 m.
Q3=124 [N] c=1.1 m
Q4=20 [N]
Q5=9
Szukane:
RX, RY, RZ, MgX, MgY, MgY =?
Szukane wartości znajduje korzystając z równań równowagi dla układu przestrzennego.
Równania równowagi:
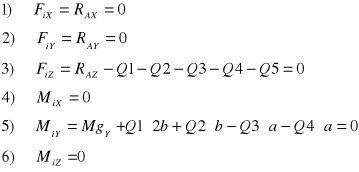
Po przekształceniach otrzymujemy:
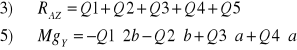
Ostatecznie:
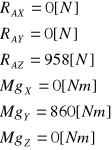
Jak wynika z równań równowagi siłami działającymi na płytę są:
RAZ - siła dociskająca,
Mgy - moment gnący (wyrywa).
Układ sił z płytą jest przedstawiony poniżej:
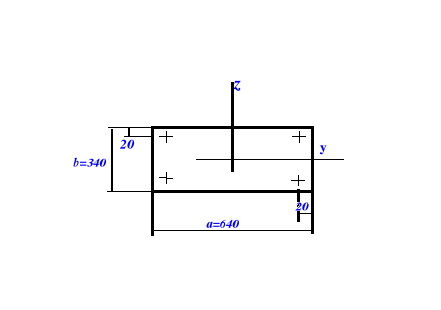
W tym przypadku nie mamy do czynienia z siłami przesuwającymi płytę , więc wzór na siłę występującą w jednej śrubie fundamentowej jest postaci:
![]()
gdzie:
Fst =a*b = 0.64 [m] * 0.34 [m]= 0.2176 [m2]
z =4 - liczba śrub,
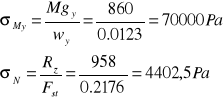
Po podstawieniu danych liczbowych otrzymujemy:
![]()
Z warunku wytrzymałościowego dla śruby mamy:![]()
Re = 300 [MPa]
x = 2![]()
Ponieważ przekrój śruby jest kołem![]()
Przekształcając warunek wytrzymałościowy otrzymuję wzór na średnicę rdzenia śruby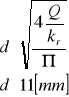
Średnica rdzenia wynosi 11 [mm]. Dobrałem śrubę M14.
6.8 Obliczenia przegubu siłownika
Siłownik połączony jest poprzez ucho i sworzeń z ramieniem manipulatora. Sworzeń jest pasowany, dlatego obliczono go z warunku na ścinanie. Sworzeń wykonany jest ze stali St5.
ks = 90 [MPa]
![]()
Warunek wytrzymałościowy![]()
Dane:
P = 1730 [N]
kt = 90 [MPa]
Z warunków wytrzymałościowych obliczam średnicę sworznia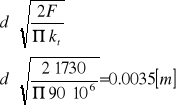
Przyjmuję średnicę sworznia d = 12 [mm]
6.9 Weryfikacja połączenia spawanego
Weryfikacji poddaję połączenie spawane korpusu górnego z korpusem dolnym manipulatora
robota.
Zakładam spoinę pachwinową o grubości 10 [mm].
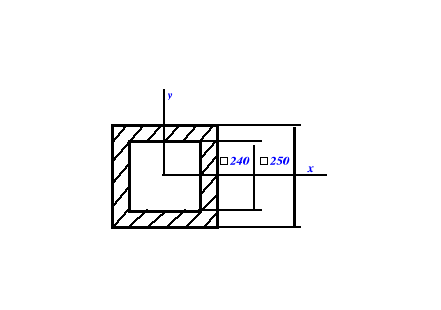
Dane:
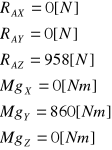
Momenty bezwładności
względem osi
Ponieważ spoina jest kwadratem Ix = Iy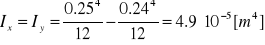
biegunowy moment bezwładności
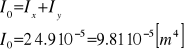
Wskaźniki wytrzymałości
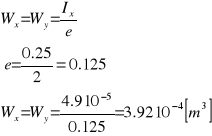
![]()
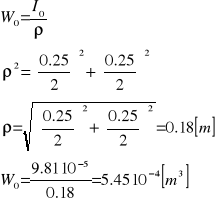
Zgodnie z PN—/B—03200 poszczególne naprężenia muszą spełniać następujący warunek![]()
Dla spoiny pachwinowej:
s = 0.8
R = 250 [MPa]![]()
Obliczenia naprężeń działających w spoinie
Dla spoiny pachwinowej występują jedynie naprężenia styczne
![]()
lub ![]()
gdzie:
F - siła
Fst - pole powierzchni spoiny
![]()
Naprężenia wynoszą odpowiednio
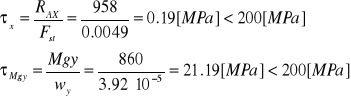
Jak wynika z przeprowadzonych wyżej obliczeń poszczególne naprężenia spełniają warunek wytrzymałościowy.
Wykres i naprężenia wypadkowe
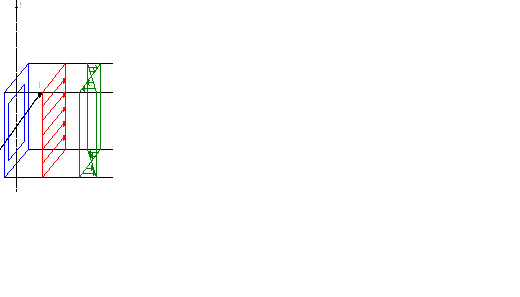
Naprężenie wypadkowe wyraża się wzorem
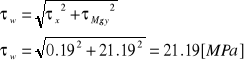
Ponieważ zgodnie z PN / B—03200 naprężenie wypadkowe będzie złożeniem kilku naprężeń i musi spełniać warunek
![]()
wobec tego
![]()
Z obliczeń wynika, że również warunek na naprężenia wypadkowe jest spełniony.
Opierając się na powyższej weryfikacji można stwierdzić, że połączenie spawane w postaci spoiny pachwinowej wokół obudowy manipulatora wytrzyma obciążenia jakie występują w czasie jego pracy.
1
2


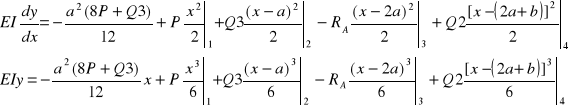
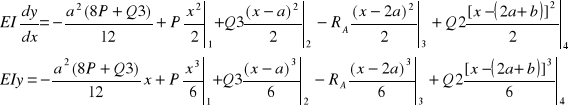
![]()
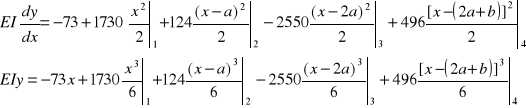
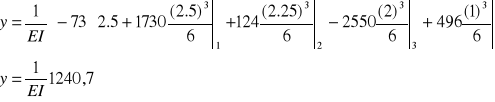
![]()
![]()
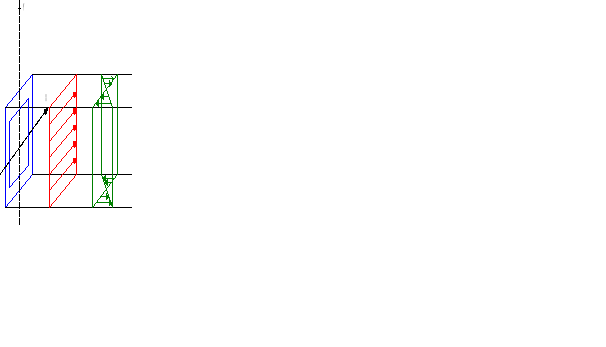

Wyszukiwarka
Podobne podstrony:
Konstruowanie katalogowe manipulatorów, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty,
Manipulator, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty
Manipulator 3, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty
Projekt pkm2, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, Projekty - multum ciulstwa
pkm, Automatyka i Robotyka, Semestr 5, PKM, projekty
pstan, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, Projekty - multum ciulstwa, Manip
man r2, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, Projekty - multum ciulstwa, Mani
man r3, Automatyka i Robotyka, Semestr 5, PKM, projekty, projekty, Projekty - multum ciulstwa, Mani
Pytania z PKM, Automatyka i Robotyka, Semestr 5, PKM, pytania
obliczenia do robota, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatoró
Kinematyka odwrotna, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatorów
Notacja Denavita, Automatyka i Robotyka, Semestr 4, Kinematyka i Dynamika Robotów i Manipulatorów, p
POLITECHNIKA ŚLĄSKA W GLIWICACH fffffff, Automatyka i Robotyka, Semestr IV, Podstawy Konstrukcji mas
projekt dla rudego, Automatyka i Robotyka, Semestr 4, Podstawy konstrukcji maszyn, Projekt
interpolacja projekt, Automatyka i Robotyka, Semestr 1, Podstawy Sterowania, projekt1-Interpolacja
Analiza cyklogramu szeregowego, Automatyka i Robotyka, Semestr 2, Robotyzacja, projekt, projekt 2
interpolacje projekt2, Automatyka i Robotyka, Semestr 1, Podstawy Sterowania, projekt1-Interpolacja
więcej podobnych podstron