Instytut Automatyzacji procesów Technologicznych

i Zintegrowanych Systemów Wytwarzania

Wydział Mechaniczny Technologiczny

Politechnika Śląska w Gliwicach

PODSTAWY STEROWANIA ROBOTÓW I MASZYN

Projekt

INTERPOLACJA

Prowadzący zajęcia:

dr inż. Agnieszka SĘKALA

Opracował:

Mariusz MUCHA, grupa dziekańska: 3, semestr: 1, kierunek: Automatyka i Robotyka

Gliwice, 00. listopad. 2005

Spis treści:

Wprowadzenie do zagadnienia…………………………………………………. 3

Dane do zadania………………………………………………………………… 4

Rozwiązanie zadania……………………………………………………………. 5

Wnioski…………………………………………………………………………. 9

1. Wprowadzenie do zagadnienia

Do wyznaczenia zaprogramowanego kształtu trajektorii służy tzw. interpolator trajektorii, którego zadaniem jest określenie współrzędnych pośrednich toru manipulatora (pomiędzy zadanymi wartościami współrzędnych pozycji początku i końca drogi), inaczej nazywanych pozycjami podporowymi. Pozycje te gwarantują zachowanie odpowiednigo kształtu drogi (toru). Danymi wejściowymi do obliczeń interpolacyjnych są: współrzędne pozycji bieżącej jako pozycji początkowe ruchu interpolowanego, współrzędne pozycji docelowej jako pozycji końca ruchu, kształt toru w przestrzeni rozpiętego pomiędzy pozycją początkową i końcową ruchu oraz prędkość z jaką ma nastąpić przemieszczenie. Rodzaj interpolacji wskazuje według jakiego wzorca matematycznego określającego kształt drogi zostaną określone punkty pośrednie (podporowe). Do podstawowych, stosowanych w sterowaniu robotów, rodzajów interpolacji należy interpolacja liniowa, kołowa (ruch po łuku okręgu) oraz interpolacja TCP. Zadaniem interpolatora jest podział całego odcinka realizowanej drogi pomiędzy pozycją początkową a końcową na etapy zwane sekcjami (wyznaczanymi w stałych odcinkach czasu). Sekcje wyznaczają kolejne punkty podporowe, czyli położenia przez które musi przejść planowana trajektoria, aby żądany kształt toru został osiągnięty. Uzyskiwane na podstawie przeliczeń interpolacyjnych współrzędne pozycji pośrednich są wartościami dyskretnymi, a wszystkie parametry potrzebne do wyliczeń są ustalane dla konkretnych warunków czasu i miejsca. W ten sposób otrzymuje się współrzędne początku i końca poszczególnych sekcji.

2. Dane do zadania

a) rysunki

Rys.1

gdzie:

x_p, y_p- współrzędne punktu P w kartezjańskim układzie współrzędnych

L- długość prostej

α- kąt nachylenia prostej do osi rzędnych układu współrzędnych

R- promień interpolacji kołowej (po łuku okręgu)

φ- miara kąta rozwarcia łuku (zakres kąta interpolacji)

Rys.2 Rys.3

b)dane liczbowe:

- punkt P: x_p=-60, y_p=100 - okrąg: R=55, φ=-60°

- prosta L: α=-135°, L=65 - tolerancja: I=0.01, A=0.01

3. Rozwiązanie zadania

a) wyznaczam kąty α oraz β:

≈0.9998 ⇒ β=arccos(0.9998)≈1.14°

≈0.9996 ⇒ α=arccos(0.9996)≈1.62°

b) Obliczam ilość punktów podporowych w ruchu interpolowanym po łuku, przy czym do wzoru wstawiam φ=60, wynika to z tego, że znak (minus) informuje jedynie o kierunku łuku zakreślanego przez promień R w układzie współrzędnych (rys.1)

≈17.8

Ilość punktów podporowych należy zaokrąglić do wartości całkowitej w górę, więc ostatecznie: a=18

c) znając wartość a należy dokonać korekty wartości kąta α:

≈1.6°

d) ze wstępnej analizy danych zamieszczonych w pkt.2 można już wywnioskować, że kształt toru będzie wyglądał następująco:

Rys.4

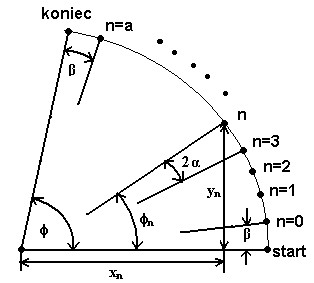
Ruch rozpoczyna się w punkcie P i przebiega po linii prostej aż do punktu K- jest to faza ruchu po linii prostej. Następnie rozpoczyna się 2 faza, w której ruch odbywa się w kierunku oznaczonym na rys.4 jako (-φ) po łuku okręgu zakreślanego przez promień R z początku układu współrzędnych (SX'Y').

e) punkt startowy (K) interpolacji kołowej ma współrzędne (0;55) licząc od początku układu współrzędnych SX'Y'.

Następnie według następującego algorytmu:

φ_n=β+n2α

x_n=(R+A)*cos(φ_n)

y_n=(R+A)*sin(φ_n)

gdzie: n - zmienia się w zakresie od 0 do a

φ_n - zmienia się w zakresie od β do (φ-β)

obliczam współrzędne punktów podporowych interpolacji:

n	φn	xn	yn
0	1.14	54.99	-1.09
1	4.34	54.85	-4.16
2	7.54	54.53	-7.21
3	10.74	54.04	-10.25
4	13.94	53.38	-13.25
5	17.14	52.56	-16.21
6	20.34	51.57	-19.12
7	23.54	50.43	-21.97
8	26.74	49.12	-24.75
9	29.94	47.66	-27.45
10	33.14	46.06	-30.07
11	36.34	44.31	-32.59
12	39.54	42.42	-35.02
13	42.74	40.4	-37.33
14	45.94	38.25	-39.53
15	49.14	35.98	-41.6
16	52.34	33.61	-43.54
17	55.54	31.12	-45.35
18	58.74	28.54	-47.02

tabela 1.

Znak (minus) przy kolejnych wartościach y_n wynika z kierunku ruchu (rys.4), aby otrzymać właściwe wartości, należy dokonać symetrii osiowej toru względem osi SX'

Współrzędne punktu końcowego (T) interpolacji obliczam opierając się na rys.2:

x_t=(R+A)*cos φ=27.5

y_t=(R+A)*sin φ=-47.64

f) wyznaczam współrzędne punktu (K), który jest punktem końcowym ruchu po prostej i jednocześnie punktem początkowym ruchu po łuku okręgu:

Rys.5

β=180°-α=180°-135°=45°

sinβ=Δy/L ⇒ Δy=L*sinβ=65*sin45°=45.96

cosβ=Δx/L ⇒Δx=L*cosβ=65*cos45°=45.96

x_k=x_p-Δx= -60-45.96= -105.96

y_k=y_p-Δy= 100-45.96= 54.04

więc ostatecznie punkt startowy (K) ma współrzędne: (-105.96;54.04)

g) otrzymałem różne współrzędne punktu startowego:

z ppkt. (e) wynika, że: K(0;55)

natomiast z ppkt. (f) wynika, że : K(-105.96;54.04)

W rzeczywistości jest to ten sam punkt a jego przesunięcie wynika z faktu, że w ppkt. (e) współrzędne tego punktu zostały obliczone wzgłedem układu SX'Y', a w ppkt. (f) względem układu 0XY. Współrzędne punktów podporowych także zostały wyliczone względem początku układu współrzędnych SX'Y'. W związku z tym aby ustalić ich rzeczywiste położenie należy dokonać translacji współrzędnych (tabela 1)o wartość:

[-105.96-55;54.04-0]=[-160.96;54.04] /co wynika z różnych współrzędnych punktu

startowego (K)/

każdego punktu (x_n;y_n) na punkt (x_n'';y_n'') według następującego algorytmu:

(x_n'';y_n'')=(-160.96+x_n;54.04+y_n)

h) współrzędne punktów podporowych interpolacji po łuku okręgu liczone względem początku układu współrzędnych 0XY są następujące:

- współrzędne punktu startowego: K(-105.96;54.04)

- współrzędne punktów podporowych:

n	xn''	yn''
0	-105.97	52.95
1	-106.11	49.88
2	-106.43	46.83
3	-106.92	43.79
4	-107.58	40.79
5	-108.4	37.83
6	-109.39	34.92
7	-110.53	32.07
8	-111.84	29.29
9	-113.3	26.59
10	-114.9	23.97
11	-116.65	21.45
12	-118.54	19.02
13	-120.54	16.71
14	-122.71	14.51
15	-124.98	12.44
16	-127.35	10.5
17	-129.84	8.69
18	-132.42	7.02

tabela 2

-współrzędne punktu końcowego

(x_t'';y_t'')=(-160.96+x_t;54.04+y_t)=(-133.46;6.4)

8

---