Wydział: MT Gliwice, dn. 2.04.2001r

Kierunek: AiR

Sem.: VI

Gr. Dziek.: III

Mateja Mateusz

Podstawy Sterowania Robotów

Zadanie proste kinematyki

Wstęp teoretyczny

Skutecznym aparatem matematycznym wykorzystywanym w robotyce jest tzw. Notacja D-H (Denavita-Hartenberga), oparta na rachunku macierzowym. Służy ona do analiz względnego położenia w innym układzie. Wygodnie jest tu wprowadzić współrzędne jednorodne. Współrzędnymi jednorodnymi nazywać będziemy czwórkę dowolnych liczb spełniających warunek taki, że:

1. wszystkie nie mogą być jednocześnie równe zeru,

2. wszystkie są związane poprzez współrzędne kartezjański i zachodzi pomiędzy nimi relacja (dla warunku, że zawsze
   ),

.

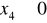
Parametr
nazywany jest czasami współczynnikiem skali. Wykorzystując współrzędne jednorodne, wektor
opisujący położenie punktu w układzie kartezjańskim można teraz zapisać w postaci:

przy warunku, że
.

Rozważmy teraz przypadek, w którym pozycja P(x,y,z,a,b,c) jest zdefiniowana w układzie U_B. Z kolei położenie układu U_B w układzie U_A jest określone wektorem położenia
. Zachodzi pytanie, jak można określić pozycję P układzie U_A?

Aby to zagadnienie wyjaśnić, musimy zastanowić się najpierw nad sposobem zapisu formalnego orientacji (położenie określa wektor
). Orientację przestrzenną układu współrzędnych związanego z pozycją P określają trzy kąty a, b, c.

Ponieważ osie układu kartezjańskiego, przyjętego w naszych rozważaniach jako podstawowego, są do siebie wzajemnie prostopadłe, więc wektory jednostkowe tych osi również. Przyjmijmy zatem, ze orientację układu współrzędnych pozycji P, względem nieruchomego układu odniesienia wyraża tzw. Macierz kosinusów kierunkowych, gdzie każdy element tej macierzy jest rzutem wektora jednostkowego, związanego z układem obróconym na kierunek wektora jednostkowego układu odniesienia, co przedstawia iloczyn skalarny tych dwóch wektorów.

Wykorzystując macierz kosinusów kierunkowych można powiedzieć, że jeżeli znane jest położenie początku układu U_B w układzie U_A, znana jest macierz kosinusów kierunkowych C układu U_B względem U_A, to położenie dowolnej pozycji P określone w układzie U_B można wyrazić U_A poprzez zależność macierzową:

gdzie poszczególne parametry x_n oznaczają współrzędne jednorodne, n=1,2,3,4, przy czym:

- położenie początku układu U_B w układzie U_A,

- wsp. Pozycji P wyrażone w układzie U_B,

- wsp. Pozycji P w układzie U_A,

- macierz kosinusów kierunkowych określających orientację układu U_B względem U_A.

Jak łatwo zauważyć, przedstawiona zależność zawiera w drugiej macierzy (o wymiarze 4x4) dodatkowy wiersz, nie omawiany wcześniej, składający się z trzech zer. Przez dodanie dodatkowego wiersza uzyskano macierz symetryczną 4x4, dzięki czemu umożliwiono wykonanie iloczynu macierzowego odpowiednio do zasad rachunku macierzowego.

Jeżeli przyjmiemy, że:

,

uzyskamy równość czwartej wsp. w obu układach, wtedy:

gdzie parametry x, y, z oznaczają w odpowiednio wartości współrzędnych wyrażone w odpowiednim układzie wsp.

Powyższe wyrażenie opisuje ogólna zasadę, która mówi, że przemieszczenie dokonane w jednym układzie, a wyrażone w drugim jest równe iloczynowi macierzy orientacji i położenia drugiego układu względem pierwszego oraz wektora położenia w drugim układzie. Proces określania współrzędnych jakiegoś elementu w jednym układzie współrzędnych na podstawie znajomości położenia (relacji) tego układu w innym nazywamy przekształceniem lub transformacją współrzędnych. Proces wyrażania układu U_B względem układu U_A będziemy oznaczać jako T_AB (transformacja).

Zadanie

Znaleźć współrzędne punktu leżącego na końcu ostatniego ogniwa.

Dane:

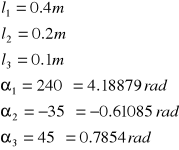
Macierz rotacji pierwszego układu dana jest wzorem

,

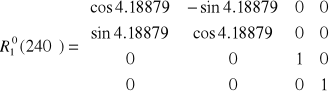
natomiast macierz przesunięcia układu:

.

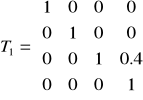
Dla drugiego układu (prostopadłego do poprzedniego - γ=90°) macierz obrotu wygląda następująco:

,

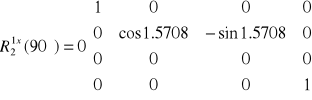
macierz transformacji

.

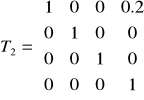
Macierz rotacji następnego układu (bez przesunięcia):

.

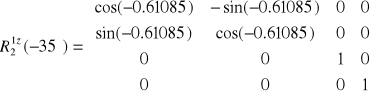
Macierze (rotacji i transformacji) czwartego pokazano poniżej

,

.

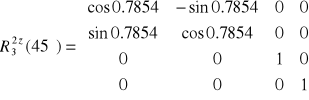
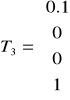
Mając wszystkie macierze rotacji i transformacji, możemy przystąpić do obliczenia wektora punktu (współrzędnych szukanego punktu).

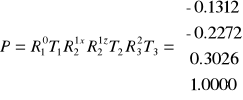
Wartości współrzędnych wyliczonych metodą wykreślną podano poniżej:

x=-0.1200m

y=-0.2025m

z=0.3650m

Jak widać, największy błąd sięga około 6cm. Mógł on zostać spowodowany pewną niedokładnością przyrządów (zwłaszcza kątomierza), co w połączeniu z podziałką 1:2,5 zaowocowało tak dużym błędem. Należy jeszcze przypomnieć, że w wartości współrzędnej „z”, zawarte są błędy pochodzące od wsp. „x” i „y”. Współrzędna zetowa została wyznaczona jako ostatnia, ponieważ wcześniej należało ustalić długości dwóch ostatnich ramion robota (ich rzutów na oś y).

---