SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ
KATEDRA TECHNIKI POŻARNICZEJ		LABORATORIUM HYDROMECHANIKI
Ćwiczenie nr: 8 Temat: Badanie pomp i ich współpracy szeregowej i równoległej	Pluton: II	Marczak Andrzej
				Grupa: A
Prowadzący: kpt. mgr inż. E. Pawlak	Data wykon. 02.03.2003 r.	Data złożenia 16.03.2003 r.	Ocena:

1. Cel ćwiczenia.

Celem tego ćwiczenia jest określenie charakterystyki pompy, oraz wykazanie jakie są różnice przy połączeniu szeregowym i równoległym pomp.

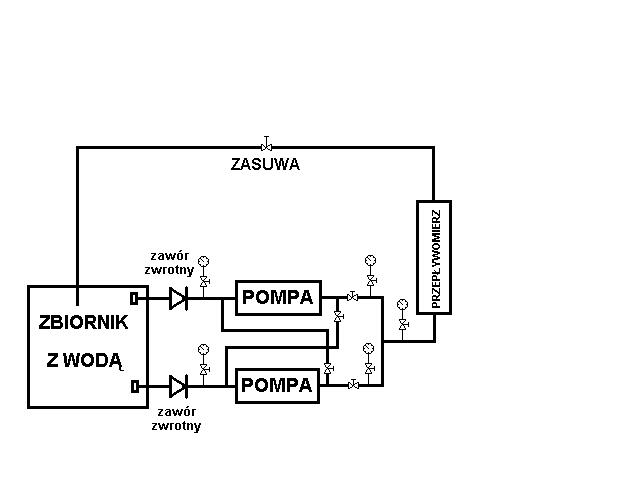
2. Schemat stanowiska pomiarowego.

3. Tabela obliczeniowa - praca jednej pompy.

Lp	k [%]	Hss [msw]	Htł [msw]	Ns [kW]	Qobl [l/s] 4,4l/s=100%	Hu [msw]	Nu [kW]	p [%]
1	55	-7	5	1,02	2,42	-2	-0,04	-6,03
2	50	-2	12	1,08	2,20	10	0,21	29,91
3	45	-1	18	1,11	1,98	17	0,33	45,74
4	40	-1	24	1,14	1,76	23	0,39	52,63
5	35	0	29	1,11	1,54	29	0,43	59,6
6	30	0	34	1,08	1,32	34	0,44	62,68
7	25	0	37	1,02	1,10	37	0,39	58,82
8	20	0	40	0,96	0,88	40	0,37	59,29
9	15	0	43	0,9	0,66	43	0,28	47,86
10	10	1	44	0,78	0,44	44	0,19	37,48

4. Przykładowe obliczenia.

H_u obliczono ze wzoru:

H_u = H_ss + H_tł [msw]

Przykład (pkt 2): H_u = -2+12 = 10[msw]

N_u obliczono ze wzoru:

Przykład (pkt 2):

_p obliczono ze wzoru:

_s = 0,65

Przykład (pkt 2): _p) = 0,33 / (1,11 * 0,65) = 0,45

5. Tabela obliczeniowa -praca dwóch pomp połączonych równolegle.

Lp	k [%]	Hss1 [msw]	Hss2 [msw]	Htł [msw	Ns [kW]	Qobl [l/s] 4,4l/s=100%	Hu [msw]	Nu [kW]	p [%]
1	95	-1	0	14	2,16	4,18	13	0,53	37,75
2	90	-1	0	16	2,22	3,96	15	0,58	40,19
3	85	-1	0	20	2,28	3,74	19	0,69	46,56
4	75	0	0	26	2,22	3,3	26	0,84	58,21
5	70	0	0	29	2,22	3,08	29	0,87	60,29
6	65	0	0	30	2,16	2,86	30	0,84	59,83
7	60	0	0	32	2,16	2,64	32	0,82	58,4
8	55	0	0	34	2,1	2,42	34	0,8	58,61
9	45	0	0	38	1,98	1,98	38	0,73	56,72
10	40	0	0	40	1,92	1,76	40	0,69	55,29
11	35	0	0	41	1,86	1,54	41	0,61	50,45
12	25	1	0	44	1,68	1,1	45	0,48	43,96
13	15	1	0	45	1,44	0,66	46	0,29	30,98
14	5	1	0	46	1,14	0,22	47	0,1	13,5

6. Przykładowe obliczenia.

H_u obliczono ze wzoru:

H_u = H_ss1 + H_tł[msw]

Przykład (pkt 2): H_u = -1 + 16 = 15 [msw]

N_u obliczono ze wzoru:

Przykład (pkt 3):

_p obliczono ze wzoru:

_s = 0,65

Przykład (pkt 2):

7. Tabela obliczeniowa - praca dwóch pomp połączonych szeregowo.

Lp	k [%]	Hss1 [msw]	Htł1 [msw]	Htł2 [msw	Ns [kW]	Qobl [l/s] 4,4l/s=100%	Hu [msw]	Nu [kW]	p [%]
1	56	-2	4	6	1,98	2,46	4	0,09	6,99
2	50	-2	12	22	2,10	2,2	20	0,43	31,5
3	45	-1	18	34	2,16	1,98	33	0,64	45,58
4	40	-1	24	46	2,22	1,76	45	0,77	53,36
5	35	0	30	58	2,22	1,54	58	0,87	60,29
6	30	0	34	68	2,10	1,32	68	0,88	64,47
7	25	0	38	74	2,04	1,1	74	0,79	59,58
8	20	0	40	80	1,92	0,88	80	0,69	55,29
9	15	0	43	89	1,68	0,66	89	0,57	52,2
10	10	0	45	90	1,44	0,44	90	0,38	40,6
11	5	1	46	92	1,20	0,22	93	0,2	25,64

8. Przykładowe obliczenia.

H_u obliczono ze wzoru:

H_u = H_ss1 + H_tł[msw]

Przykład (pkt 2): H_u = -2 + 22= 20 [msw]

N_u obliczono ze wzoru:

Przykład (pkt 2):

_p obliczono ze wzoru:

_s = 0,65

Przykład (pkt 2):

9. Wnioski

Analizując wyniki badań można stwierdzić, że największą wysokość podnoszenia uzyskuje się przy szeregowym połączeniu dwóch pomp, natomiast przy połączeniu równoległym uzyskuje się najkorzystniejsza moc hydrauliczną. Charakterystyczne jest, że dla połączenia szeregowego i pompy pracującej pojedynczo, przebieg charakterystyki mocy hydraulicznej jest porównywalna dla poszczególnych wartości Q. Wysokość podnoszenia maleje wraz ze wzrostem natężenia przepływa, natomiast sprawność i moc hydrauliczna osiągają maksimum około połowy wartości Q.

---