SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ
KATEDRA TECHNIKI POŻARNICZEJ		LABORATORIUM HYDROMECHANIKI
Ćwiczenie nr:13 Temat: Badanie procesu zasysania wody.	Pluton: III	Imię i nazwisko: Krzysztof Stachurski
					Grupa: A
Prowadzący: bryg. mgr inż. Wojciech Zegar	Data wykonania: 30.03.2002		Data złożenia: 11.04.2002	Ocena:

Cel ćwiczenia

Metody pomiarowe zastosowane w ćwiczeniu pozwalają na określenie charakterystyki pompy próżniowej, charakterystyki nieszczelności, teoretycznego czasu ssania i rzeczywistego czasu ssania na podstawie zarejestrowanych nieustalonych przebiegów zmian ciśnienia w rozpatrywanym układzie.

Przykładowe obliczenia

Obliczenie stałej „C” potrzebnej do wyznaczenia wydatku „Q”.

p∙V = m∙R∙T

ponieważ: m = C∙p,

to

gdzie: V - objętość zbiornika = 40∙10^-3 [m³],

R - stała gazowa = 287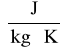

T - temperatura = 293 [K]

C =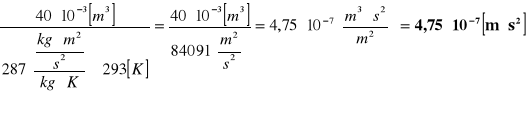

Obliczenie pochodnej w danym punkcie dla pompy pracującej w układzie szczelnym

x₁=10 mm

y₁=13 mm

Obliczenie wydatku „Q”

Q =

gdzie:

C - stała,

- wartość pochodnej wyznaczonej metodą graficzno - obliczeniową

Q = 4,75∙10^-7[m∙s²]∙1,3 [hPa/s] = 6,175∙10^-5[Pa∙m∙s] =

6,175 ⋅ 10^-5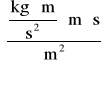
= 6,175∙10^-5

Tabele obliczeniowe

Dla pompy pracującej w układzie szczelnym

L.p.	Δp [hPa]
	300	1,8	8,55 ∙ 10^-5
	400	1,3	6,175 ∙ 10^-5
	600	0,7	3,32 ∙ 10^-5
	700	0,4	1,94 ∙ 10^-5
	800	0,2	1,95 ∙ 10^-5

Obliczenie pochodnej w danym punkcie dla pompy pracującej w układzie ze średnią nieszczelnością

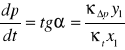
x₁=20 mm

y₁=25 mm

κ_Δ
p=0,4

κ_t=0,185

Dla pompy pracującej ze średnią nieszczelnością

L.p.	Δp [hPa]
	250	2,70	12,8∙ 10^-5
	200	2,16	10,26∙ 10^-5
	150	2,37	11,3∙ 10^-5
	100	1,51	7,18∙ 10^-5
	50	1,08	5,13∙ 10^-5

Q = 4,75∙10^-7[m∙s²]∙2,16 [hPa/s] = 1,26∙10^-4[Pa∙m∙s] =

1,26 ⋅ 10^-4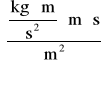
= 1,26∙10^-4

Obliczenie pochodnej w danym punkcie dla pompy pracującej w układzie z małą nieszczelnością

x₁= 10 mm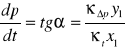

y₁= 8 mm

κ_Δp=
4

κ_t=0,45

Dla pompy pracującej z mała nieszczelnością

Lp.	Δp [hPa]
	500	7,1	33,7 ∙ 10^-5
	400	11,55	54,8 ∙ 10^-5
	300	8,88	42,2 ∙ 10^-5
	200	8,88	42,2 ∙ 10^-5
	100	5,33	25,3 ∙ 10^-5

Q = 4,75∙10^-7[m∙s²]∙ 7,1 [hPa/s] = 3,37 ∙10^-4[Pa∙m∙s] =

3,37 ⋅ 10^-4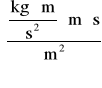
= 3,37 ∙10^-4

Wnioski:

W wyniku otrzymanych danych widzimy, że wraz ze wzrostem podciśnienia maleje wydajność pompy, rośnie natomiast ilość powietrza zasysanego przez nieszczelności układu. Dla różnych nieszczelności sporządzone zostały charakterystyki Q_n = f(∆p). Maksymalne podciśnienie jakie może wytworzyć pompa przedstawia punkt przecięcia wykresu Q_p = f(∆p),
z wykresem Q_n = f(∆p), przy danej nieszczelności. Na podstawie przeprowadzonego ćwiczenia należy stwierdzić, że podciśnienie maksymalne jest tym niższe, im większa jest nieszczelność. Stosunkowo mała dokładność metody wyznaczania pochodnej wynika z różnic pomiędzy maksymalnymi podciśnieniami zarejestrowanymi podczas przeprowadzania ćwiczenia,
a wyznaczonymi na wykresie. Na podstawie otrzymanych danych sporządzone zostały charakterystyki Q_p = f(∆p), oraz Q_n = f(∆p).

---