Sprawozdanie nr 11
Prow. A. Sterna
Zad. 1: Zbudować automat asynchroniczny o działaniu:
-po pierwszym wciśnięciu przycisku lampka zapala się
-po drugim wciśnięciu przycisku lampka bez zmian
-po trzecim wciśnięciu przycisku lampka gaśnie.
Wykres czasowy automatu:
Stany: |
1 |
2 |
3 |
4 |
5 |
6 |
1 |
|
|
|
|
|
|
|
|
X1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W automacie występuje jedno wejście i jedno wyjście, z tabeli wyszło 6 stanów.
Tablica przejść stanów:
Kodowanie stanów:
Tablica przejść:
Siatka Karnaugh'a dla wyjść Y
Tablica przejść RS
Tablica przejść z przejściami RS
Siatki Karnaugh'a dla każdego R i S:
Równania do siatek :
Zjawisko hazardu występuje przy R3 i S3, więc trzeba dodać element łączący obszary:
Przekształcenia równań:
Schemat :
stan |
z0 |
z1 |
Y |
1 |
1 |
2 |
0 |
2 |
3 |
2 |
1 |
3 |
3 |
4 |
1 |
4 |
5 |
4 |
1 |
5 |
5 |
6 |
1 |
6 |
1 |
6 |
0 |
Aby uniknąć zjawiska wyścigów, należy zakodować tak, by w przejściu zawsze zmieniał się tylko jeden bit. 6 stanów można zapisać na 3 bitach.
stan |
Q1 |
Q2 |
Q3 |
1 |
0 |
0 |
0 |
2 |
0 |
0 |
1 |
3 |
0 |
1 |
1 |
4 |
0 |
1 |
0 |
5 |
1 |
1 |
0 |
6 |
1 |
1 |
1 |
Q1 Q2 Q3 |
z0 |
z1 |
Y |
0 0 0 |
0 0 0 |
0 0 1 |
0 |
0 0 1 |
0 1 1 |
0 0 1 |
1 |
0 1 1 |
0 1 1 |
0 1 0 |
1 |
0 1 0 |
1 1 0 |
0 1 0 |
1 |
1 1 0 |
1 1 0 |
1 1 1 |
1 |
1 1 1 |
0 0 0 |
1 1 1 |
0 |
Q1Q2 Q3 |
|
01 |
11 |
10 |
|
0 |
1 |
1 |
- |
1 |
1 |
1 |
0 |
- |
![]()
Q(t) |
Q(t+1) |
R |
S |
0 |
0 |
- |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
- |
z |
Q1 |
Q2 |
Q3 |
Q(t+1)1 |
Q(t+1)2 |
Q(t+1)3 |
R1 |
S1 |
R2 |
S2 |
R3 |
S3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
- |
0 |
- |
0 |
- |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
- |
0 |
0 |
1 |
0 |
- |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
- |
0 |
0 |
- |
0 |
- |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
- |
- |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
- |
0 |
- |
- |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
- |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
- |
0 |
- |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
- |
0 |
- |
0 |
0 |
- |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
- |
0 |
0 |
- |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
- |
0 |
0 |
- |
- |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
- |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
- |
0 |
- |
0 |
- |
zQ1
|
00 |
01 |
11 |
10 |
00 |
- |
- |
- |
- |
01 |
- |
1 |
- |
- |
11 |
- |
- |
0 |
- |
10 |
0 |
0 |
0 |
- |
zQ1 Q2Q3 |
00 |
01 |
11 |
10 |
00 |
0 |
0 |
0 |
0 |
01 |
0 |
0 |
0 |
0 |
|
0 |
0 |
- |
0 |
10 |
1 |
- |
- |
0 |
zQ1 Q2Q3 |
00 |
01 |
11 |
10 |
00 |
|
- |
- |
0 |
01 |
1 |
0 |
- |
0 |
11 |
- |
- |
- |
- |
10 |
- |
- |
0 |
- |
zQ1 Q2Q3 |
00 |
01 |
11 |
10 |
00 |
- |
0 |
0 |
- |
01 |
0 |
- |
0 |
- |
11 |
0 |
|
0 |
0 |
10 |
0 |
0 |
1 |
0 |
zQ1
|
00 |
|
|
10 |
00 |
- |
- |
- |
0 |
01 |
|
1 |
- |
0 |
11 |
0 |
- |
0 |
1 |
10 |
- |
- |
0 |
- |
zQ1 Q2Q3 |
|
|
11 |
10 |
00 |
0 |
0 |
0 |
1 |
01 |
- |
0 |
|
- |
11 |
- |
0 |
- |
0 |
10 |
0 |
0 |
1 |
0 |
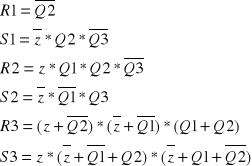
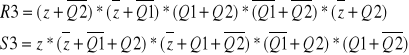
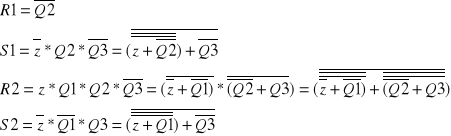
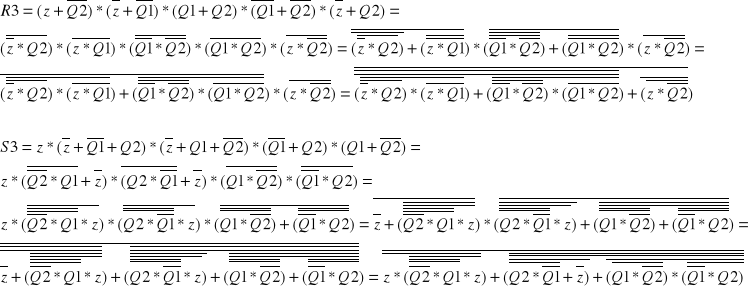
R1
S1
R2
S2
R3
S3
Wyszukiwarka
Podobne podstrony:
sprawko 11, Studia, PWR, 3 semestr, Logika układów cyfrowych, laboratoria
sprawko 3a, Studia, PWR, 3 semestr, Logika układów cyfrowych, laboratoria
sprawko 10, Studia, PWR, 3 semestr, Logika układów cyfrowych, laboratoria
sprawko 10a, Studia, PWR, 3 semestr, Logika układów cyfrowych, laboratoria
sprawko 4, Studia, PWR, 3 semestr, Logika układów cyfrowych, laboratoria
TECHNIKA CYFROWA - sprawko lab 1, Studia, PWR, 4 semestr, Podstawy techniki mikroprocesorowej, labor
TECHNIKA CYFROWA - sprawko lab 4, Studia, PWR, 4 semestr, Podstawy techniki mikroprocesorowej, labor
TECHNIKA CYFROWA - sprawko lab 5, Studia, PWR, 4 semestr, Podstawy techniki mikroprocesorowej, labor
Niezawodność i diagnostyka układów cyfrowych, Studia, PWR, 4 semestr, Niezawodność i diagnostyka ukł
programowalny dzielnik częśtotliwości, Studia, Informatyka, Semestr III, Teoria Układów Cyfrowych, L
podsekcja radzio, Studia, Informatyka, Semestr III, Teoria Układów Cyfrowych, Laboratorium, lab4
203 rejestry, Politechnika Wrocławska - Materiały, logika ukladow cyfrowych, sprawozdania
Notatki2, Studia - Socjologia - Semestr I, LOGIKA
Grupa, Studia Pwr, Semestr 1, Psychologia (wykład)
Sprawozdanie44b, Studia, PWR, 3 semestr, Fizyka 2
sterna,logika układów cyfrowych L, Komputerowa synteza automatu z parametrem wewnętrznym
Porównanie procesów poznawczych i emocjonalnych, Studia Pwr, Semestr 1, Psychologia (wykład)
Urządzenia peryferyjne lab2, Studia, PWR, 5 semestr, Urządzenia peryferyjne, laboratorium
Przykładowe zadania na 2 kolokwium z programowania w języku C, Studia, PWR, 1 semestr, Podstawy prog
więcej podobnych podstron