CAŁKI POWIERZCHNIOWE

Powierzchnie

Powierzchnia jest to zbiór punktów (x,y,z) spełniających pewne równanie, które jest klasy
i ma jedną z trzech postaci:

* postać uwikłana:

** postać jawna:

*** postać parametryczna: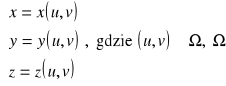
- obszar w

Definicja

Wektorem normalnym do powierzchni S w punkcie
nazywamy niezerowy wektor prostopadły do wszystkich krzywych leżących na S i przechodzących przez
.

Jeśli S zadana jest w postaci:

* uwikłanej, to

,

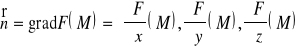
gdzie M jest punktem zwyczajnym, tzn. gradient w tym punkcie nie zeruje się, gradF(M)
.

** jawnej, to przekształcając równanie
otrzymujemy postać uwikłaną

gdzie

i korzystając ze wzoru na wektor normalny w przypadku * dostajemy

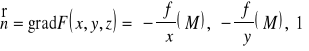
*** parametrycznej, to w punkcie jednokrotnym powierzchni S, tzn. punkcie odpowiadającym tylko jednej parze
wektor normalny zadany jest wzorem

przy założeniu, że wyznacznik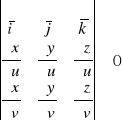
.

Jeśli dany jest wektor normalny
do powierzchni S, to płaszczyzna
styczna do powierzchni S w punkcie
jest postaci

.

Zatem w przypadku *

.

Natomiast w przypadku **

,

stąd

.

Definicja

Powierzchnia gładka jest to powierzchnia, która w każdym swoim punkcie ma płaszczyznę styczną, która zmienia się w sposób ciągły przy zmianie punktu styczności.

Warunkiem wystarczającym gładkości powierzchni jest by równanie określające powierzchnię było klasy
oraz w przypadku, gdy powierzchnia jest zadana w postaci uwikłanej - by nie zawierała punktów osobliwych oraz w przypadku, gdy jest określona w postaci parametrycznej - by nie zawierała punktów wielokrotnych i
.

Przykład

Równanie
lub równoważne
określa powierzchnię stożkową.

Istotnie, jeśli
, to
i przekrój płaszczyzną
jest okręgiem o środku w punkcie
i promieniu
. Natomiast jeśli
, to

zatem przekrój powierzchni płaszczyzną
jest dwoma prostymi
i
.

Widać, że powyższa powierzchnia nie jest gładka, ponieważ w punkcie
nie istnieje płaszczyzna styczna. W istocie, dla funkcji

.

równanie
jest klasy
oraz

.

Ponieważ

zatem punkt
jest punktem osobliwym.

Definicja

Płatem nazywamy figurę określoną równaniem
, D - domknięty obszar jednospójny,
.

Definicja

Płat nazywamy gładkim, gdy
.

Definicja

Powierzchnia regularna jest to powierzchnia, którą można podzielić na skończenie wiele płatów gładkich.

Przykład

- powierzchnia regularna

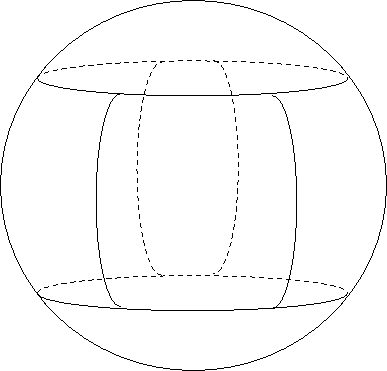
- półsfera nie jest powierzchnią regularną, bo dla jej brzegu (największego okręgu) nie istnieją pochodne cząstkowe, natomiast sfera jest powierzchnią regularną bo można ją podzielić na 6 płatów gładkich.

4

---