Nazwisko i imię	Numer grupy	Numer ćwiczenia	Temat ćwiczenia
Anna Miszkiel	IX	9/ 11	Wyznaczenie modułu Younga metodą wydłużeń i strzałki ugięcia

Ciała w zależności od budowy wewnętrznej dzielimy na jednorodne i niejednorodne oraz izotropowe i anizotropowe.

Ciała jednorodne to ciała, w których element objętości ma takie same właściwości fizykochemiczne (m.in. właściwości mechaniczne, elektryczne, optyczne).

Ciała izotropowe to ciała, których właściwości fizykochemiczne są jednakowe we wszystkich pomyślanych kierunkach ciele.

W ciałach anizotropowych właściwości te zależą od kierunków wybranych w ciele. Do ciał jednorodnych anizotropowych należą czyste ciała krystaliczne z wyjątkiem kryształów układu regularnego. Przykładem ciała niejednorodnego anizotropowego jest drewno, włosy, włókna

Zjawisko odkształceń sprężystych ciał niejednorodnych anizotropowych jest zjawiskiem złożonym, zależnym od wielu parametrów charakteryzujących właściwości sprężyste ciał.

Ciało nazywamy sprężystym, a jego odkształcenie spowodowane oddziaływaniem zewnętrznym- odkształceniem sprężystym, jeśli zanika ono całkowicie po ustąpieniu tych oddziaływań. Zgodnie z prawem Hooke'a odkształcenia sprężyste są wprost proporcjonalne do wywołujących je oddziaływań zew., tzn. zależą od nich w sposób liniowy.. Przy dostatecznie małych odkształceniach praktycznie wszystkie ciała można uważać za sprężyste.

W przypadku małych sił występuje równoważenie się sił zewnętrznych i sił wewnętrznych. Po usunięciu takich sił zew. ciało wraca do pierwotnego kształtu i objętości. W tych warunkach mówimy o odkształceniach sprężystych. Lub doskonale sprężystych.

Przy wzroście siły zewnętrznej aż do pewnej wartości granicznej rośnie też stopniowo odkształcenie badanego ciała zachowując swój charakter sprężysty . Po przekroczeniu granicznej wartości siły zew. ( zależnej od rodzaju badanego ciała) powstają odkształcenia niesprężyste. Po usunięciu sił zew. Siły wew. Nie sprowadzają ciała do pierwotnego kształtu i objętości. Pozostaje w ciele trwałe odkształcenie.

Przy omawianiu właściwości sprężystych ciał zamiast pojęć siły zew. i wew. stosuje się najczęściej pojęcie ciśnienia (zew.) i napięcia (wew.). Wielkości te kojarzymy z działaniem siły ( odpowiednio zew lub wew) na jednostkę powierzchni. Jeżeli siła- F wzdłuż osi pręta (ściaskająco lub rozciągająco), wówczas jest prostopadła do przekroju poprzecznego- S i jej stosunek do powierzchni tego przekroju nazywamy ciśnieniem lub naprężeniem p. Innymi słowy ciśnienie (naprężenie) p w przypadku równomiernego rozkładu siły F na powierzchnię S wynosi

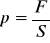
lub przy siłach o rozkładzie nierównomiernym p=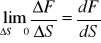
gdzie ∆F- siła działająca na mały element powierzchni ∆S. Ciśnienie jest wielkością wektorową o kierunku zgodnym z kierunkiem działania siły F. Naprężenie i ciśnienie wyrażamy w tych samych jednostkach. jednostkach układzie SI jednostką naprężenia i ciśnienia jest niuton na metr kwadratowy ( N/m²) zwany też paskalem.

ODKSZTAŁCENIA SPRĘŻYSTE

Odkształcenia mogą mieć różny charakter. Można tu wymienić wydłużenia (skrócenia, rozszerzenia objętościowe (skurczenia), zgięcia, skręcenia itp.

Za miarę odkształcenia związanego ze zmianą długości przyjmujemy względny przyrost długości ε, zdefiniowany jako stosunek przyrostu długości ∆l (np. pręta) do długości pierwotnej l₀.

Idealne odkształcenia objętościowe występują wtedy gdy kształt ciała zostaje zachowany, natomiast gęstość ulega zmianie (np. ciało kuliste pozostaje ciałem kulistym, ale ma już mniejszą lub większą objętość). Za miarę odkształcenia objętościowego przyjmujemy względny przyrost objętości θ zdefiniowany jako stosunek przyrostu objętości do objętości pierwotnej V₀ :

Z idealnym odkształceniem postaciowym mamy do czynienia wtedy, gdy gęstość dowolnie małego elementu ciała pozostaje niezmienna, zmianie ulega kształt.

Odkształcenia sprężyste występujące w przyrodzie mają na ogół charakter złożony

PRAWO HOOKE'A

Jest to prawo obowiązujące dla małych odkształceń. Zgodnie z prawem Hooke'a odkształcenia sprężyste są wprost proporcjonalne do wywołujących je oddziaływań zew., tzn. zależą od nich w sposób liniowy.. Przy dostatecznie małych odkształceniach praktycznie wszystkie ciała można uważać za sprężyste.

Prawo to mówi, że stosunek naprężenia do związanego z nim odkształcenia jest wielkością stałą dla danego materiału. Stosunek ten nazywamy modułem sprężystości. Prawo Hooke'a przy wydłużeniach wyraża się wzorem

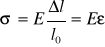
, gdzie σ- ozn ciśnienie (naprężenie) normalne, wynikające z działania siły prostopadłej do powierzchni, E- moduł sprężystości przy wydłużeniu zwany modułem Younga. Znajomość modułu dla danego materiału pozwala obliczyć przyrost długości prętów lub drutów, wywołany działaniem siły normalnej F_n

gdzie S- przekrój poprzeczny badanego pręta lub drutu. Stąd
. Po przekształceniu tego wzoru otrzymujemy
lub zastępując
przez ε mamy

. Odkształcenie ε jest wprost proporcjonalne do naprężenia p (
- współczynnik proporcjalności).

Prawo Hooke'a zarówno w formie
jak i

uzależnia odkształcenie od naprężenia. Z tej zależności często korzystamy np. przy cechowaniu wag sprężonych oraz dynamometrów.

W odniesieniu do odkształceń objętościowych zmiana dp ciśnienia gazu podczas małej zmiany dV jego objętości jest wprost proporcjonalna do odkształcenia względnego objętości

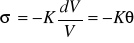
gdzie K- moduł sprężystości objętościowej gazu. Znak minus występujący w równaniu przypomina, że dodatnim przyrostom ciśnień (naprężeń) odpowiadają ujemne przyrosty objętości: im większe zastosujemy ciśnienie ściskające, tym bardziej ciało się kurczy. W przypadku odkształceń postaciowych prawo Hooke;a wyraża się wzorem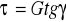
, gdzie τ- ciśnienie styczne do powierzchni , G- moduł sprężystości postaciowej

Ze wzorów
,
,
wynika, że moduły sprężystości wyrażają się w jednostkach ciśnienia (wielkości θ, ε i tgγ są niemianowane)

Wartości liczbowe modułów ciał sprężystych są bardzo duże ze względu na małą ich odkształcalność

Wyznaczenie modułu Younga

skąd
. Ze wzoru tego wynika, że jeśli ∆l=l₀ , to
lub
tzn. że moduł Younga liczbowo jest równy takiemu naprężeniu zewnętrznemu- p, które spowodowałoby wydłużenie drutu ∆l równe długości początkowej l₀ (czyli drut miałby długość podwójną).

Moduł Younga stali strunowej wynosi E ≈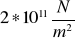
. Wyrażając to w jednostkach już nielegalnych, lecz ciągle jeszcze bliższych naszej wyobraźni, otrzymamy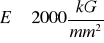
. Oczywiście takiego obciążenia (2000kG)- drut milimetrowy nie wytrzyma. Już przy naprężeniu dziesięć razy mniejszym odkształcenia przestają podlegać prawu Hooke'a, gdyż przestają być sprężyste, po czym szybko zostaje osiągnięta granica wytrzymałości.

Wartości modułów Younga oraz granice sprężystości i wytrzymałości materiałów podają tablice fizyczne i warto je przejrzeć.

Wyznaczenie modułu Younga metodą wydłużeń

Badany drut zawieszamy pionowo, po czym jego wolny koniec obciążamy stopniowo, np. jednakowymi odważnikami, notując kolejne wydłużenia drutu ∆l₁, ∆l₂, … odpowiadające poszczególnym przyrostom siły ( ciężaru ). Jeżeli odważniki będą jednakowe, to kolejne wydłużenia ∆l₁, ∆l₂, … będą jednakowe ( w granicach błędu pomiarowego ). Gdyby się okazało, że jednakowym przyrostom siły odpowiadają coraz większe wydłużenia ∆l_i, świadczyłoby to, że przekroczylibyśmy granicę stosowalności prawa Hooke'a. Pomiar należałoby powtórzyć z drutem „ nie zmęczonym „, stosując oczywiście mniejsze siły.

Podczas zdejmowania kolejnych odważników drut powinien wrócić poprzez te same ∆l_i (teraz ujemne) do długości początkowej l₀.

Rozwiązanie techniczne metody wydłużeń może być też inne, np. napinanie drutu może odbywać się za pomocą śruby, pomiar siły napinającej (F) - za pomocą dynamometr, a pomiar wydłużenia (∆l) - za pomocą mikroskopu wyposażonego w odpowiednią skalę. Należy wstępnie napiąć badany drut siłą 30N, nastawić mikroskop na ostre widzenie „odnośnika” (w polu widzenia czarne duże kratki na tle mikroskali), a w razie potrzeby pole widzenia dodatkowo oświetlić. Następnie należy stopniowo napinać drut przyrostami siły np. po 20N, obserwując przesuwanie się dowolnej linii odnośnika (prawej lub lewej krawędzi tej linii) względem działek mikroskali i licząc je. Jedna działka oznacza 0,02mm.

Wyznaczenie modułu Younga metodą strzałki ugięcia.

Belka o przekroju prostokątnym jest podzielona na równoległe warstwy (a'b', a”b” itd.) wzdłuż osi podłużnej. Podczas uginania belki górne warstwy będą ulegać ściskaniu (skracaniu, dolne zaś rozciąganiu). Ze względu na ciągłość zachodzącego zjawiska musi istnieć taka warstwa AB, której długość nie ulegnie zmianie. Warstwa taka nazywa się warstwą obojętną i w niej znajduje się oś podłużna belki lub pręta.

W poszczególnych warstwach belki, podczas jej uginania występuje jednokierunkowy stan naprężenia. Wynika z tego, że poszczególne warstwy wzdłuż uginanej belki nie wywierają na siebie żadnego nacisku, przekroje poprzeczne natomiast nachylają się do siebie o pewien kąt α, lecz nadal pozostają płaskie. Jeżeli belka lub pręt są poddane „czystemu” ugięciu, to we wszystkich przekrojach stan napięcia będzie taki sam, wobec czego promień ugięcia R dla warstwy obojętnej będzie wszędzie jednakowy.

Na podstawie wyników doświadczalnych stwierdzono, że promień ugięcia R jest wprost proporcjonalny do grubości i szerokości belki (czyli do jego przekroju poprzecznego), a odwrotnie proporcjonalny do długości belki i siły uginającej.

Strzałka ugięcia jest to różnica pomiędzy położeniem warstwy obojętnej (belki lub pręta) przed odkształceniem i po dokształceniu w miejscu maksymalnego ugięcia. Można ją wyrazić następującym wzorem: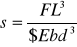
stąd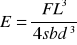
gdzie: L - długość belki (między punktami podparcia), b - szerokość belki, d - grubość belki, F - siła powodująca ugięcie, s - strzałka ugięcia.

---