POLITECHNIKA WROCŁAWSKA

LABORATORIUM MECHANIKI GÓROTWORU

TRÓJOSIOWY STAN NAPRĘŻENIA

WYKONALI:

WSTĘP TEORETYCZNY

Jeżeli na elementarny sześcian wycięty z obciążonego elementu konstrukcji działają w trzech prostopadłych kierunkach naprężenia normalne σ_x, σ_y, σ_z, wówczas mówimy o trójosiowym stanie naprężenia.

W przypadku badania skał na ściskanie w trójosiowym stanie naprężenia, stosujemy próbkę walcową o smukłości 1 i badanie przeprowadzamy w aparacie trójosiowego ściskania. W tym stanie występują trzy rodzaje naprężeń; główne, normalne i ścinające.

Można rozróżnić trzy typy badań trójosiowego ścinania:

• Test klasyczny

(następuje bezpośrednie ścięcie próby).

• Test wielokrotnego zniszczenia

(próba zostaje kilkakrotnie obciążona

nim zostanie ścięta).

• Test ciągłego zniszczenia

(obciążenie próby następuje powoli

i nie ma wyraźnej granicy ścięcia próby).

Do obliczeń można zastosować dwa kryteria określające stan naprężeń w trójosiowym stanie naprężenia:

• Kryterium Coulomba - Mohra,

Mając wyznaczone naprężenia σ₁ i σ₃ wyznacza się za pomocą kół Mohra kąt tarcia wewnętrznego i spójność. Przy wykreślaniu kół Mohra przyjmuje się układ współrzędnych prostokątnych , w którym oś rzędnych stanowią naprężenia ścinające, oś odciętych naprężenia główne. Odkładając na osi pierwszą parę naprężeń głównych wyznaczamy na tej osi dwa punkty, których odległość od siebie wyznaczy średnicę koła. Środek koła wyznacza wzór (σ₁ + σ₃)/2 a promień (σ₁ - σ₃)/2. Wyznaczonym promieniem należy wykreślić półkole leżące nad osią naprężeń. W analogiczny sposób wyznacza się drugie i trzecie półkole.

Po wykreśleniu kół należy przeprowadzić obwiednię do otrzymanego zespołu kół, która jest zazwyczaj linią prostą. Miejsce przecięcia się obwiedni z osią τ daje wartość spójności a kąt nachylenia tej prostej do osi naprężeń jest kątem tarcia wewnętrznego. Wzór na opór skały na ścinanie będzie miał postać:

τ - opór skały na ścinanie

σ - naprężenie normalne

φ - kąt tarcia wewnętrznego

c- spójność

Dla jednoosiowego stanu naprężenia

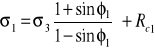
Dla trójosiowego stanu naprężenia

• Kryterium Hoeka - Browna,

PRZEBIEG BADANIA W APARACIE TRÓJOSIOWEGO ŚCINANIA

Pomiar w aparacie trójosiowego ściskania polega na; umieszczeniu badanej próbki w odpowiedniej cienkiej gumowej osłonie, której średnica powinna być równa średnicy próbki. Próbkę układa się na trzonie podstawy aparatu i naciąga na trzon dolny koniec osłony gumowej. Na górnym końcu próbki ustawia się tłoczek, na który również naciąga się osłonę gumową. Przygotowaną w ten sposób próbę wkładamy do komory Carmana, którą dociska się do podstawy śrubami dociskowymi w celu uzyskania odpowiedniego uszczelnienia komory. Następnie za pomocą pompki wtłacza się do komory olej i po napełnieniu spręża się olej do odpowiedniego ciśnienia przez dalsze pompowanie. Po uzyskaniu żądanego ciśnienia obciąża się próbkę osiowo i doprowadza się do ścięcia próbki.

SCHEMAT APARATU TRÓJOSIOWEGO ŚCINANIA

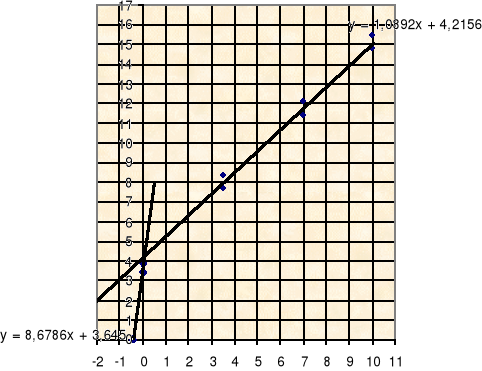
OPRACOWANIE WYNIKÓW DLA WĘGLA BRUNATNEGO

Dane z badania przeprowadzonego w aparacie trójosiowego ścinania:

R_r=0,42

σ3	σ1
0	3,88
0	3,41
3,5	8,38
3,5	7,74
7	12,12
7	11,42
10	15,48
10	14,81

Obliczenia przeprowadzamy wykorzystując kryterium Coulomba - Mohra

R_c = 3,64

Znając wartości R_r i R_c (wytrzymałość na jednoosiowe rozciąganie i jednoosiowe ściskanie) wartość spójności i kąta tarcia wewnętrznego możemy policzyć ze wzorów:

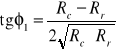
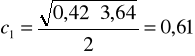
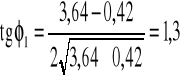
Przebieg badania przedstawiamy za pomocą kół Mohra.

Wynik badania aproksymujemy dwuliniowo i odczytujemy wartości c₁ , φ₁ , c₂ , φ₂ ,

Opór skały na ścinanie dla jednoosiowego stanu naprężenia wyraża się wzorem :

gdzie: φ₁= 52° c₁=0,61

Opór skały na ścinanie dla trójosiowego stanu naprężenia wyraża się wzorem:

gdzie: φ₂= 4° c₂=1,7

Zależność σ₁ od σ₃ wynosi dla jednoosiowego stanu naprężenia wynosi:

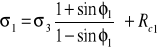
a dla trójosiowego:

gdzie:

Zależności te możemy przedstawić na wykresie:

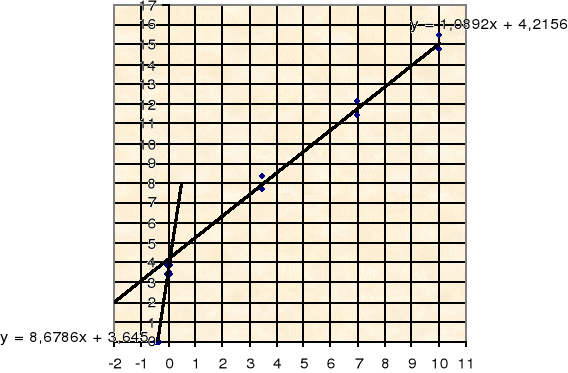
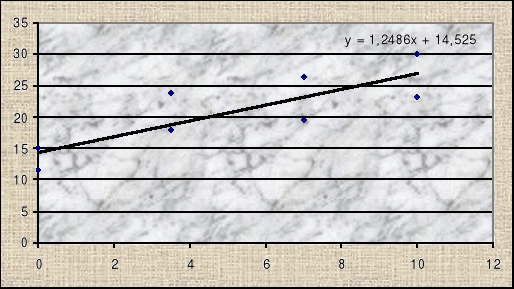
Opracowanie wyników stosując kryterium Hooka-Browna

Funkcję tę możemy przekształcić na funkcję liniową:

następnie podstawiając y=(σ₁-σ₃)² a=m_iR_c x=σ₃ b=R_c² otrzymujemy wzór prostej w postaci

x=σ3	y=(σ1-σ3)^2
0	15,0544
0	11,6281
3,5	23,8144
3,5	17,9776
7	26,2144
7	19,5364
10	30,0304
10	23,1361

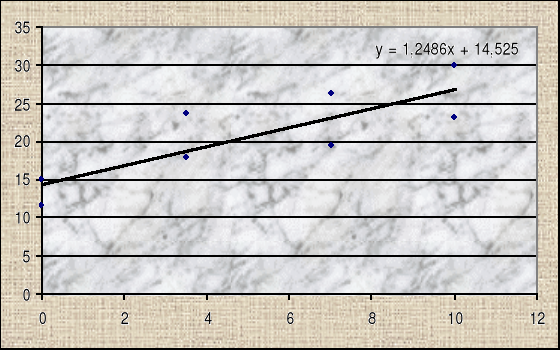
Z wykresu odczytujemy wartości b=R_c²

i obliczamy wartość parametru m.:

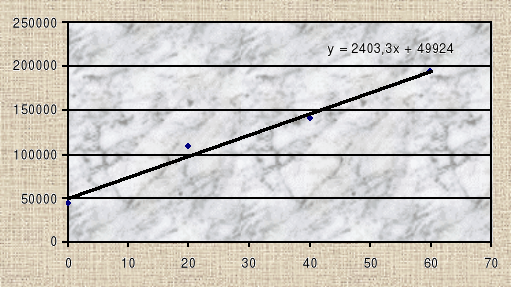
OPRACOWANIE WYNIKÓW DLA PIASKOWCA SILNIE ZWIĘZŁEGO.

Dane z badania w aparacie trójosiowego ściskania:

σ3	σ1
0	210,7
20	349,7
40	415,8
60	500,2

R_r = 11,8

R_c = 210,7

Znając wartości R_r i R_c wartość spójności i kąta tarcia wewnętrznego możemy policzyć ze wzorów:

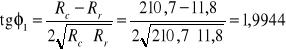
Przebieg badania przedstawiamy za pomocą kół Mohra.

Wynik badania aproksymujemy dwuliniowo i odczytujemy wartości c₁ , φ₁ , c₂ , φ₂ ,

Opór skały na ścinanie dla jednoosiowego stanu naprężenia wyraża się wzorem :

gdzie: φ₁= 64° c₁=24,4

Opór skały na ścinanie dla trójosiowego stanu naprężenia wyraża się wzorem:

gdzie: φ₂= 41° c₂=48,85

Zależność σ₁ od σ₃ wynosi dla jednoosiowego stanu naprężenia wynosi:

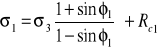
a dla trójosiowego:

gdzie:

Zależności te możemy przedstawić na wykresie:

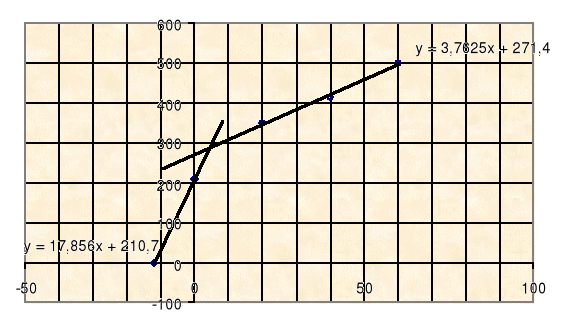
Opracowanie wyników stosując kryterium Hooka-Browna

x=σ3	y=(σ1-σ3)^2
0	44394,49
20	108702,1
40	141225,6
60	193776

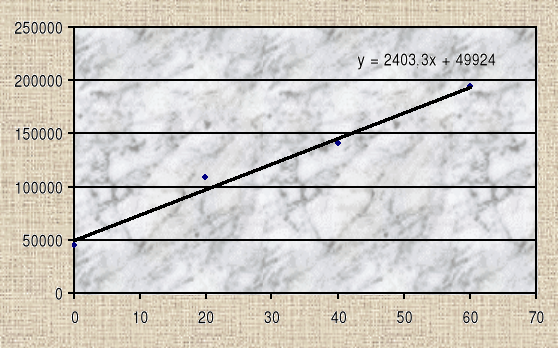
Z wykresu odczytujemy wartości b=R_c²

i obliczamy wartość parametru m.:

σ₁

σ₁1

σ₃

σ₂1

σ₁

σ₁

σ₁

σ₃

σ₃

σ₃

---