Prawo Hooke'a - prawo mechaniki określające zależność odkształcenia od naprężenia. Głosi ono, że odkształcenie ciała pod wpływem działającej na niego siły jest wprost proporcjonalne do tej siły. Współczynnik między siłą a odkształceniem jest często nazywany współczynnikiem (modułem) sprężystości.

Ta prawidłowość, sformułowana przez Roberta Hooke'a (1635-1703) w formie "ut tensio sic vis", pozostaje prawdziwa tylko dla niezbyt dużych odkształceń, nie przekraczających tzw. granicy Hooke'a (zwanej też granicą proporcjonalności), i tylko dla niektórych materiałów. Prawo Hooke'a zakłada też, że odkształcenia ciała, w reakcji na działanie sił, następują w sposób natychmiastowy i całkowicie znikają, gdy przyłożone siły przestają działać. Takie uproszczenie jest wystarczające jedynie dla ciał o pomijalnie małej lepkości.

Osiowy stan naprężenia i odkształcenia

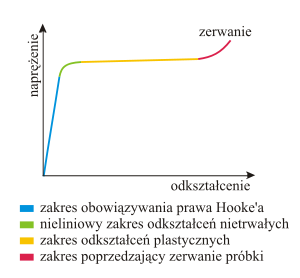
Zależność odkształceń od naprężeń z zaznaczonym zakresem stosowalności prawa Hooke'a

Najprostszym przykładem zastosowania

prawa Hooke'a jest rozciąganie statyczne pręta.

Względne wydłużenie takiego pręta jest wprost

proporcjonalne do siły przyłożonej do pręta,

do jego długości i odwrotnie proporcjonalne

do pola przekroju poprzecznego pręta.

Współczynnikiem proporcjonalności jest moduł Younga E

, więc:

gdzie:

F - siła rozciągająca,

S - pole przekroju,

Δl - wydłużenie pręta,

l - długość początkowa.

W przypadku pręta bądź drutu o stałej średnicy można to wyrazić prościej: wydłużenie względne jest proporcjonalne do działającej siły.

Stosując definicje odkształcenia i naprężenia można powiedzieć, że względne wydłużenie jest proporcjonalne do naprężenia, co można zapisać:

gdzie:

- odkształcenie względne,

- naprężenie.

Trójwymiarowy stan naprężenia i odkształcenia

Prawo Hooke'a dla ogólnego, trójwymiarowego układu naprężeń w przypadku materiału izotropowego może być zapisane w postaci układu równań:

dla odkształceń liniowych

dla odkształceń kątowych własnych

gdzie:

ε - odkształcenie liniowe w punkcie,

σ - naprężenie liniowe w punkcie,

γ - odkształcenie postaciowe (kątowe) w punkcie,

τ - naprężenie kątowe w punkcie,

G - współczynnik sprężystości postaciowej (poprzecznej) lub moduł Kirchhoffa.

E - moduł Younga

ν - współczynnik Poissona

Zapis tensorowy

W ujęciu ogólnym (dla materiału anizotropowego) jako współczynnik proporcjonalności stosuje się tensor sztywności c

lub tensor podatności b

Moduł Younga

Moduł Younga (E) - inaczej moduł odkształcalności liniowej albo moduł sprężystości podłużnej (w układzie jednostek SI) - wielkość określająca sprężystość materiału. Wyraża ona, charakterystyczną dla danego materiału, zależność względnego odkształcenia liniowego ε materiału od naprężenia σ, jakie w nim występuje w zakresie odkształceń sprężystych.

Jednostką modułu Younga jest paskal, czyli N/m².

Moduł Younga jest hipotetycznym naprężeniem, które wystąpiłoby przy dwukrotnym wydłużeniu próbki materiału, przy założeniu, że jej przekrój nie ulegnie zmianie (założenie to spełnione jest dla hipotetycznego materiału o współczynniku Poissona υ = 0).

Wielkość została nazwana na cześć angielskiego fizyka i lekarza Thomasa Younga.

W przypadku materiału izotropowego moduł Younga powiązany jest z innymi stałymi materiałowymi:

gdzie: G - moduł Kirchhoffa,

υ - współczynnik Poissona,

B - moduł Helmholtza,

λ i μ - stałe Lamégo.

Przybliżone wartości modułu Younga dla różnych materiałów
Materiał	Moduł Younga (E) GPa
Guma	0,01-0,10
Polietylen (LDPE)	0,2
Polipropylen (PP)	1,5-2,0
Osłonka wirusa	1-3
Poli(tereftalan etylenu) (PET)	2,0-2,5
Polistyren (PS)	3,0-3,5
Nylon	2-4
Drewno dębowe (wzdłuż włókien)	11
Beton (ściskany)	>27
Magnez (Mg)	45
Stop glinu (aluminium) (Al)	69
Szkło (SiO2, Na2CO3, CaCO3)	72
Mosiądz (Cu, Zn) i Brąz (Cu, Sn)	103-124
Tytan (Ti)	105-120
Kompozyt z włókna węglowego	150
Żelazo kute i stal	190-210
Wolfram (W)	400-410
Węglik krzemu (SiC)	450
Węglik tytanu (TiC)	450-650
Miedź	100-115
Cynk	84
Ołów	16
Cyna	47
Nanorurka	>1 000^[1]
Diament (C)	1 050-1 200

Siła sprężystości - siła, która powoduje powrót odkształconego ciała do pierwotnego kształtu lub objętości. Dla małych odkształceń siła sprężystości jest proporcjonalna do odkształcenia, co wyraża prawo Hooke'a, które dla odkształcenia liniowego można przedstawić wzorem:

gdzie

- zmiana długości (wydłużenie lub skrócenie) ciała,

- współczynnik sprężystości sprężyny wyrażany w N/m,

- siła sprężystości.

Minus we wzorze oznacza, że siła sprężystości ma zwrot przeciwny do zwrotu zmiany długości ciała. Dlatego powoduje jej powrót do pierwotnego kształtu.

W ogólnym przypadku dowolnej bryły o dowolnej strukturze, siły sprężystości ciała mają bardziej skomplikowany charakter, zarówno przestrzenny, jak i co do kierunku, a zamiast współczynnika sprężystości stosuje się tensor sztywności. Jest to spowodowane tym, że różne siły (np. ściskające, ścinające) i momenty sił (np. skręcające) działające na ciało mogą powodować różne odkształcenia, przy czym nie zawsze kierunek działania siły pokrywa się z kierunkiem odkształcenia

Krzywa naprężenia

rys.1 Krzywa naprężenia dla stali

rys.2 Krzywa naprężenia dla polimeru

Krzywa naprężenia ilustruje, jaka jest współzależność naprężenia i wydłużenia materiału. Krzywa ta może mieć różny kształt w zależności od substancji, jej kształtu i warunków, w jakich poddawana jest naprężeniu, na przykład od temperatury. Można na tej krzywej wyróżnić pewne charakterystyczne strefy:

• Odcinek prostoliniowy. Jest to zakres stosowania prawa Hooke'a.

• (2) Granica sprężystości. Dla mniejszych naprężeń ciało powraca do pierwotnego kształtu po usunięciu naprężenia. Zakres sprężystości zawiera w sobie również zakres stosowalności prawa Hooke'a.

• (4) Zakres plastyczności. W tym zakresie naprężeń, po ustaniu naprężenia pozostaje trwałe odkształcenie ciała.

• (5) Obszar płynięcia kończący się punktem zerwania (3). Przy naprężeniach z tego zakresu materiał zaczyna zachowywać się jak ciecz i ulega dalszemu odkształcaniu nawet przy zmniejszeniu naprężenia ulegając w końcu zerwaniu.

Poszczególne zakresy mogą mieć rożny rozmiar dla różnego typów materiałów, co więcej, nie wszystkie muszą wystąpić w krzywej naprężenia.

Równie ważną informacją dotyczącą materiału jest kształt ścieżki odciążenia czyli kształt krzywej jaka się tworzy kiedy po obciążeniu tylko do pewnej wartości zaczynamy zmniejszać obciążenie. Z punktu widzenia teorii wyróżnia się trzy możliwe, wyidealizowane zachowania:

1. sprężyste - krzywa odciążenia pokrywa się z krzywą obciążenia czyli materiał wraca do swojego pierwotnego kształtu.

2. plastyczne - krzywa odciążenia jest prostą, która przy braku obciążenia pozostawia w materiale trwałe odkształcenia plastyczne (por. wartość ε_o na Rys. 2). Cechą charakterystyczną typowego zachowania plastycznego jest nachylenie krzywej odciążenia w punkcie przecięcia osi ε identyczne z nachyleniem ścieżki obciążenia pierwotnego (krzywa odciążenia jest przesunięta względem krzywej obciążenia o wartość odkształcenia ε_o bez istotnej zmiany kąta nachylenia względem osi ε).

3. uszkodzenie (degradacja) materiału - odciążenie następuje po prostej zmierzającej do początku układu współrzędnych. Przy ponownym obciążeniu krzywa obciążenia różni się od początkowej gdyż w materiale wystąpiły wewnętrzne uszkodzenia i jest on mniej sztywny. Przy ponownym obciążeniu naprężenie rośnie liniowo dokładnie po prostej odciążenia aż do maksymalnego naprężenia, które osiągnięto w poprzednim procesie obciążenia.

Oprócz tego występują kombinacje różnych zachowań: np. materiały sprężysto-plastyczne czy materiały plastyczne z degradacją.

Kształt krzywej naprężenia (i odciążenia) jest podstawą klasyfikacji materiałów na

• sprężyste w których po zdjęciu obciążenia materiał wraca do pierwotnego kształtu. Materiały sprężyste mogą wykazywać zakres liniowy, opisany prawem Hooke'a, kiedy wykres jest liniowy jak i zakres nieliniowy, gdzie zależność naprężenie-odkształcenie nie jest funkcją liniową ale przy odciążeniu materiał dalej wraca do stanu nienaprężonego. Określenie materiał sprężysty nie mówi w jaki sposób materiał się niszczy, mówi tylko, że posiada zakres sprężysty. Ponieważ większość materiałów taki zakres posiada więc określenie to oznacza w praktyce, że rozpatrujemy materiał w zakresie sprężystym.

• plastyczne w których po zdjęciu obciążenia pozostają trwłe odkształcenia a materiał nie wraca do swojego pierwotnego kształtu. Formalnie należałoby rozróżnić materiały plastyczne i materiały sprężysto-plastyczne. Często określenie materiał plastyczny jest skrótowym określeniem dla materiału sprężysto-plastycznego. Wtedy, ponieważ materiał sprężysto-plastyczny posiada początkowy wyraźny odcinek sprężysty, więc w praktyce określenie to oznacza materiał, który przed zniszczeniem wykazuje wyraźne płynięcie plastyczne i zdolność do redystrybucji naprężeń w wyniku płynięcia plastycznego jest wykorzystywana w projektowaniu.

• kruche w których po odcinku sprężystym następuje zniszczenie w wyniku dekohezjii. W praktyce oznacza materiał, który nie posiada cech plastycznych.

Podział ten jest nieostry i są materiały, które trudno zaliczyć do którejś z tych grup. Przykładem może być polimer, którego krzywą naprężeń pokazuje rys. 2. Obszar sprężystości przechodzi tu płynnie w obszar plastyczności. Innym przykładem może być beton, który przy ściskaniu wykazuje własności plastyczne a przy rozciąganiu jest kruchy i wyraźnie się degraduje.

Materiały sprężyste

Dla materiałów sprężystych, w dużym zakresie naprężeń, pozostają one sprężyste (długi odcinek pierwszy). Zakres sprężystości może ograniczać się tylko do zakresu stosowalności prawa Hooke'a, co widać na rys. 1 dla stali. Zakres plastyczności występuje i jest wykorzystywany na przykład do wyciągania cienkich drutów z prętów. W materiałach sprężystych można precyzyjnie określić ich wytrzymałość, czyli maksymalne naprężenie, po którym musi nastąpić zerwanie - jest to naprężenie odpowiadające najwyższemu punktowi krzywej. Punkt zerwania też jest precyzyjnie określony. Materiałami sprężystymi są m. in. metale i niektóre tworzywa sztuczne.

Materiały plastyczne

W materiałach plastycznych zakres sprężystości jest bardzo mały, w przeciwieństwie do zakresu plastyczności. Trudno jest w tych materiałach określić wytrzymałość i punkt zerwania. Do materiałów plastycznych zalicza się m.in. glinę, plastelinę, oraz praktycznie wszystkie grunty.

Materiały kruche

Materiały takie mają dość mały zakres sprężystości. Brak jest zakresu plastyczności. Do materiałów należy szkło, ceramika.

---