Laboratorium Katedry Inżynierii Procesowej POLITECHNIKA OPOLSKA		Imię i nazwisko studenta: Rok i kierunek studiów: Grupa laboratoryjna: Rok akademicki/semestr:	3 Inżynieria środowiska 3 2004/2005 / VI
Laboratorium z Inżynierii Procesowej Ćwiczenie nr 1 Temat : WYZNACZANIE WSPÓŁCZYNNIKA WNIKANIA CIEPŁA PODCZAS KONWEKCJI WYMUSZONEJ GAZU W RURZE.
Ćwiczenie odrobiono dnia: 01.03.2005	Sprawozdanie złożono dnia: 05.04.2005			Ocena:

• Cel ćwiczenia

Celem ćwiczenia jest eksperymentalne wyznaczenie współczynnika wnikania ciepła podczas burzliwej konwekcji wymuszonej gazu w rurze oraz ocena wpływu prędkości przepływu gazu na wartość tego współczynnika.

• Opis metodyki prowadzenia pomiarów:

Po sprawdzeniu poziomu wody w wytwornicy pary włączyliśmy urządzenie pomiarowe, następnie zaworem regulacyjnym ustawiliśmy na rotametrze wymagany strumień powietrza. Po stabilizowaniu się temperatury na wlocie i wylocie dokonaliśmy ich odczytu. Czynność tą powtórzyliśmy dla różnych wartości strumienia powietrza.

• Stanowiska pomiarowego:

Głównym elementem jest rekuperator typu „rura w rurze”. Rura wewnętrzna jest wykonana z miedzi. Do przestrzeni międzyrurowej doprowadzona jest para wodna nasycona która kondensuje na wewnętrznej rurze miedzianej. Para wytwarzana jest w kotle. Rurą wewnętrzną przepływa powietrze tłoczone dmuchawą, regulowane zaworem i mierzone rotametrem. Zainstalowane termometry pozwalają na pomiar temperatury.

• Zestawienie uzyskanych wyników pomiarów:

Rura wewnętrzna : - materiał rury: miedź - średnica zewnętrzna: Φ 16 mm = 0,016 m - grubość ścianki: 1 mm = 0,001 m - długość strefy skraplania pary: 1 m Rodzaj skraplającej się pary: para wodna nasycona
Strumień powietrza			Temperatura powietrza na wlocie	Temperatura powietrza na wylocie	Temperatura kondensacji	Temperatura na rotametrze
Działki	m^3/h	m^3/s	^oC	^oC	^oC	^oC
200	9,1987	0,002555	25	74	95	21
300	12,6587	0,003516	34	73	95	23
400	16,1187	0,004477	35	72	95	23
500	19,5787	0,005439	34	70	95	22
600	23,0387	0,006400	33	68	96	22
700	26,4987	0,007361	32	67	96	21
800	29,9587	0,008322	31	65	96	21

• Opracowanie i analiza uzyskanych wyników:

1. Wyznaczenie wartości zmierzonych współczynnika wnikania ciepła.

Na przykładzie pierwszego pomiaru.

- Strumień powietrza

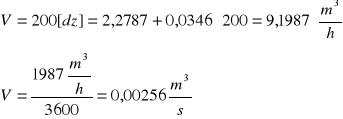
- gęstość, lepkość, ciepło właściwe i współczynnik przenikania odczytane z tablic dla średniej arytmetycznej wartości temperatury powietrza na wlocie i wylocie:

t
	1,060175	0,00001965	115,195	0,02716725

- Strumień masowy

- Strumień wnikającego ciepła

- Określenie temperatur

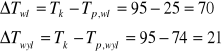
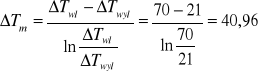
-Powierzchnia wnikania ciepła

- Wartości zmierzone współczynnika wnikania ciepła

- prędkość przepływu

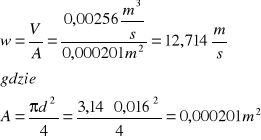
Zestawienie wyników dla wszystkich pomiarów :

Lp	Temperatura średnia powietrza	Gęstość	Lepkość	Ciepło właściwe	współczynnik przewodzenia
		Tp
		[^­^oC]	[kg/m3]	[Pas]	[J/(kgK)]	[W/(mK)]
1	49,5	1,060175	0,00001965	115,195	0,02716725
2	53,5	1,046775	0,00001982	116,035	0,02746925
3	53,5	1,046775	0,00001982	116,035	0,02746925
4	52	1,0518	0,00001976	115,72	0,027356
5	50,5	1,056825	0,00001969	115,405	0,02724275
6	49,5	1,060175	0,00001965	115,195	0,02716725
7	48	1,0652	0,00001958	114,88	0,027054

Lp	Strumień masowy	Temperatura średnia wlot	Temperatura średnia wylot	Strumień ciepła	Średnia logarytmiczna temperatur	Współczynnik wnikania ciepła (zm)
		Gp			Q
		[kg/s]	[K]	[K]	[W]	[K]	[W/(m^2K)]
1	0,002709	70	21	15,29083573	40,6985937	7,478288
2	0,0036808	61	22	16,65687637	38,2416148	8,669773
3	0,0046868	60	23	20,12202036	38,5878778	10,37937
4	0,0057202	62	26	23,83007687	41,4251233	11,45017
5	0,0067633	63	28	27,31814569	43,1603106	12,59845
6	0,0078037	64	29	31,46308474	44,2149616	14,16389
7	0,0088644	65	31	34,6238187	45,9211197	15,00766

2. Zależność pomiędzy zmierzonym współczynnikiem wnikania ciepła a prędkością przepływu powietrza.

3. Określenie współczynnika wnikania ciepła na podstawie obliczeń analitycznych.

- Liczba Prandtla

- Liczba Reynoldsa

-Liczba Nusselta, (ponieważ Re > 10000)

- Współczynnik wnikania ciepła obliczony analitycznie

Zestawienie wyników dla wszystkich pomiarów

Lp	Pr	Re	Nu
1	0,0833044	10978,213	14,5351804	24,68005506
2	0,0837404	14782,823	18,4802479	31,72740934
3	0,0837404	18823,409	22,4212859	38,49349421
4	0,0835768	23051,282	26,3462103	45,045433
5	0,0834133	27346,843	30,1819817	51,39001139
6	0,0833044	31624,944	33,8858917	57,53665566
7	0,0831413	36046,09	37,5959507	63,57005319

• Podsumowanie i wnioski:

Jak łatwo zauważyć wartość współczynnika wnikania ciepła wzrasta wraz ze wzrostem prędkości strumienia przepływającego gazu. Zależność tą widać zarówno dla współczynnika zmierzonego jak i wyznaczonego drogą analityczną, mimo że obydwie te wielkości różnią się od siebie dosyć znacząco. Wszystkie wartości otrzymane zostały w zakresie odpowiadającemu burzliwemu charakterowi przepływu powietrza.

---