TEST CHI-KWADRAT

- bazuje na rozkładzie chi-kwadrat, który - w zależności od ilości stopni swobody (k lub df) - może przedstawiać się następująco:

- na razie ważne jest, by wiedzieć, że ilość stopni swobodny, związana jest z tym ile grup obserwacji powstało w toku obserwacji (jeśli badaliśmy wzajemny wpływ dwóch zmiennych dychotomicznych, to grup obserwacji jest cztery - tabela 2x2); im więcej stopni swobody tym bardziej rozkład chi-kwadrat zbliżony jest do rozkładu normalnego!

- jak powstaje rozkład chi-kwadrat? Jest on sumą kwadratów cech, które w populacji mają rozkład normalny (Mackiewicz, Francuz, 2005: 411), wzór na rozkład chi-kwadrat mógłby wyglądać następująco:

= Z₁² + Z₂² + Z₃² + Z₄² + … + Z_N²

Symbole Z_1, Z₂ nie oznaczają konkretnych wyników, a całe zmienne! Rozkład chi-kwadrat jest podobny do rozkładu normalnego, od którego zresztą pochodzi. Ale, stosowanie rozkłady chi-kwadrat we wnioskowaniu statystycznym nie wymaga tego, by rozkład zmiennych był normalny!

Test chi-kwadrat

- jego podstawą jest porównanie dokonywane pomiędzy liczebnościami zaobserwowanymi, a liczebnościami oczekiwanymi, czyli takimi, których pojawienie się oznaczałoby brak zależności, inaczej: liczebności oczekiwane to takie, które powinny pojawić się gdyby pomiędzy zmiennymi nie istniała żadna zależność

- weźmy tabelę 2x2 i następujące wyniki, w tabeli wpisano wyniki pewnego eksperymentu, który polegał na sprawdzeniu czy istniej zależność pomiędzy płcią a poparciem dla wprowadzeniem kary śmierci.

	ZA	PRZECIW	razem:
KOBIETY	30	50	80
MĘŻCZYŹNI	40	20	60
razem:	70	70	140

W tabeli na razie znajdują się tylko liczebności obserwowane (empiryczne, zmierzone) Na pierwszy rzut oka wygląda, że jakieś różnice istnieją - kobiety rzadziej optują za karą śmierci.

A jak powinny wyglądać liczebność w każdej z wyróżnionych grup obserwacji (przypomnijmy: mamy cztery grupy obserwacji: (1) kobiety będące za karą śmierci, (2) kobiety będące przeciwne karze śmierci, (3) mężczyźni będący za karą śmierci, (4) mężczyźni będący przeciwni karze śmierci), gdyby nie zachodziła żadna różnica?

W tym celu należy:

1. ustalić proporcję liczebności każdej z czterech grup w stosunku do całości (czyli 140 osób badanych); jeśli ustalimy jaka jest ta proporcja, innymi słowy jaki jest udział każdej z czterech podgrup w całości (140), to

2. wówczas możemy obliczyć ile osób powinno przypadać na tą kategorię, na przykład, jeśli proporcja kobiet będących za karą śmierci (udział) w całości wynosiłaby 50% (zaznaczam, że tyle w rzeczywistości nie wynosi!) to liczebność oczekiwana dla tej grupy obserwacji wynosiłaby 50% x 140 = 70

3. liczebności oczekiwane mówią nam zatem o tym, jakie liczebności są czymś naturalnym, co powinno się zdarzyć, gdyby kobiety i mężczyźni, nie różnili się pod względem postaw do kary śmierci.

Jak obliczać liczebności oczekiwane. W dość prosty sposób.

1. dla kategorii `kobiety-za':

1. Po pierwsze, ustalamy, jaki jest udział kobiet (80) we wszystkich osobach badanych (140), czyli: 80/140 = 0,57

2. Po drugie, ustalamy, jaki jest udział osób będących za karą śmierci (70), we wszystkich osobach badanych (140), czyli: 70/140 = 0,50

3. Zakładamy, że te dwie cechy są niezależne (zawsze jeśli stosujemy test niezależności chi-kwadrat), zatem prawdopodobieństwo, że zajdą one jednocześnie jest równe iloczynowi ich prawdopodobieństw.

4. Tak samo rzecz się ma w przypadku obliczania proporcji kobiet-za we wszystkich osobach badanych: 0,57 x 0,50 = 0,29

5. Teraz możemy obliczyć ile powinno być kobiet-za jeśli nie zachodziłyby żadne zależności, innymi słowy: jaki wynik jest czymś naturalnym, wynikłym z proporcji osób w całości: 0,29 x 140 = 40!

2. dla kategorii `kobiety-przeciw':

1. dla kobiet: 80/140 = 0,57

2. dla osób przeciw: 70/140 = 0,50

3. proporcja kobiet-przeciw: 0,57 x 0,50 = 0,29

4. oczekiwana ilość kobiet-przeciw: 0,29 x 140 = 40!

5. (to kwestia przypadku, że liczebności oczekiwane dla kobiet-za i kobiet-przeciw są takie same, oczywiście nie zawsze tak jest!)

3. dla kategorii `mężczyźni-za':

1. dla mężczyzn: 60/140 = 0,43

2. dla osób za karą śmierci: 70/140 = 0,50

3. proporcja mężczyzn-za: 0,43 x 0,50 = 0,21

4. oczekiwana ilość mężczyzn-za: 0,21 x 140 = 30

4. dla kategorii `mężczyźni-przeciw':

1. dla mężczyzn: 60/140 = 0,43

2. dla osób za karą śmierci: 70/140 = 0,50

3. proporcja mężczyzn-przeciw: 0,43 x 0,50 = 0,21

4. oczekiwana ilość mężczyzn-przeciw: 0,21 x 140 = 30

Tabela z naniesionymi liczebnościami oczekiwanymi (w nawiasach):

	ZA	PRZECIW	razem:
KOBIETY	30 (40)	50 (40)	80
MĘŻCZYŹNI	40 (30)	20 (30)	60
razem:	70	70	140

Widać, że pewne różnice pomiędzy liczebnościami oczekiwanymi i obserwowanymi istnieją, teraz trzeba odpowiedzieć na pytanie, czy różnice te są dość duże, by można byłoby je uznać za różnice istotne statystycznie!

W tym celu stosujemy już test chi-kwadrat.

Wzór na chi-kwadrat:

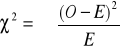
, gdzie: ∑ = znak sumy

O = liczebność obserwowana (observed)

E = liczebność oczekiwana (expected)

=
+
+
+
=

=
+
+
+
=

=
+
+
+
=

=
+
+
+
= 2,50 + 2,50 + 3,33 + 3,33 = 11,66

By wiedzieć czy obliczona wartość chi-kwadrat jest istotna statystycznie musimy jeszcze ustalić jeszcze liczbę stopni swobody (df).

Wartość tego parametru obliczamy ze wzoru:

df = (w-1) x (k-1), gdzie:

w - liczba wierszy w tabeli (w rzeczywistości zaś poziomów jednej zmiennej) k - liczba kolumn w tabeli (w rzeczywistości zaś poziomów drugiej zmiennej)

W naszym przypadku:

df = (2-1) x (2-1) = 1x1 = 1

Dopiero teraz możemy skorzystać z tablic rozkładu chi-kwadrat, wykorzystując obliczone przez nas wartości: df=1 i wartość chi² =11,66!

Z tablic odczytujemy, że dla uzyskanych przez nas wartości prawdopodobieństwo, zdiagnozowana zależność (czyli różnice w postawach wobec kary śmierci wśród kobiet i mężczyzn) jest dziełem przypadku z prawdopodobieństwem mniejszym niż 1%! W rzeczywistości prawdopodobieństwo uzyskania wartości 11,66 dla df=1 jest nawet mniejsze niż 0,001. Zdiagnozowana zależność raczej nie jest dziełem przypadku!

Szybsze sposoby na liczebności oczekiwane i chi-kwadrat.

1. liczebności oczekiwane można obliczać w następujący sposób (dla tabeli z naszego przykładu):

	ZA	PRZECIW	razem:
KOBIETY	30	50	80
MĘŻCZYŹNI	40	20	60
razem:	70	70	140

	ZA	PRZECIW	razem:
KOBIETY	= 40	= 40	80
MĘŻCZYŹNI	= 30	= 30	60
razem:	70	70	140

1. test chi-kwadrat dla tabeli 2x2 (ale tylko dla takiej tabeli!) można obliczyć także w następujący sposób:

liczebności w polach tabeli oraz liczebności brzegowe można opisać też tak:

A	B	A + B
C	D	C + D
A + C	B + D	N

w takiej sytuacji wzór na chi-kwadrat można wyrazić tak:

=

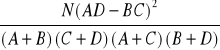
Ograniczenia w przypadku stosowania chi-kwadrat!

- w przypadku tabel 2x2, jeśli przynajmniej jedna liczebność oczekiwana jest mniejsza od 5 zaleca się stosowanie poprawki Yatesa na nieciągłość, wówczas wzór na chi-kwadrat wygląda następująco:

=

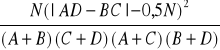
MIARY SIŁY ZWIĄZKU DLA ZMIENNYCH NOMINALNYCH

- w przypadku tabel 2x2, jako miarę siły związku stosujemy φ Yule'a, wskaźnik obliczamy ze wzoru:

sposób opisu tabeli:

A	B	A + B
C	D	C + D
A + C	B + D	N

wzór na φ Yule'a:

φ =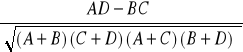

- w ten sposób opisany współczynnik φ przyjmuje wartości z przedziału od -1 do +1, ale interpretujemy tylko wartości bezwzględne!

- w przypadku niezależności zmiennych φ przyjmuje wartość równą 0

- nawet przy bardzo silnych związkach wartość φ nie osiąga wartości krańcowych równych ±1

inne możliwe sposoby obliczania φ Yule'a (z użyciem statystyki chi-kwadrat):

φ =

Obliczmy φ dla naszego przykładu:

tabela:

	ZA	PRZECIW	razem:
KOBIETY	30	50	80
MĘŻCZYŹNI	40	20	60
razem:	70	70	140

A	B	A + B
C	D	C + D
A + C	B + D	N

wzór:

φ =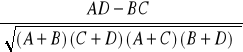

obliczenia:

φ =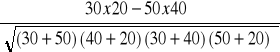

φ =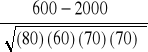
=
=
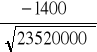
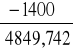
= - 0,289

- w przypadku tabel prostokątnych (2x3 i większych), jako miarę siły związku stosujemy V Cramera, wskaźnik obliczamy ze wzoru:

V =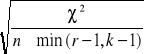
lub V=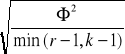

gdzie:

r - liczba wierszy (kategorii zmiennej w wierszach)

k - liczba kolumn (kategorii zmiennej w kolumnach)

min (r-1, k-1) - oznacza, że wybieramy mniejszą wartość (czyli jeśli zmienna w kolumnach ma 4 kategorie, a zmienna w wierszach ma 5 kategorii to wybieramy wartość 4)

Współczynnik V Cramera przyjmuje wartości z przedziału od 0 do +1, gdzie ) oznacza brak związku, a 1 bardzo silny związek

- dobrym rozwiązaniem jest też współczynnik kontyngencji C Pearsona, jego zaletą jest to, że możemy go stosować do tablic o dowolnej wielkości (najmniejsza liczba pól wynosi 4, czyli tablica 2x2) i o dowolnej formie (zarówno do tablic prostokątnych, jak i kwadratowych).

Jest on określony wzorem:

C =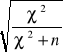
=
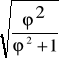
, gdzie: n - liczebność próby

- wartość chi-kwadrat

- wartość
Youle'a

Teoretycznie przyjmuje on wartości z przedziału od 0 (brak zależności) do 1 (gdy liczba pól wzrasta do nieskończoności; w praktyce, więc wartość C Pearsona nigdy nie osiąga wartości równej 1, trudno wyobrazić sobie tabelę o liczbie pól przybliżającej się choćby do nieskończoności na przykład dla tablic 3x3 wynosi 0,816).

Wartość współczynnika C Pearsona zależy bowiem do liczby wierszy i kolumn w tabeli (im więcej wierszy i kolumn tym wartość współczynnika jest wyższa), dlatego jego wartość należy rozpatrywać w zależności od wartości maksymalnej możliwej dla danej tabeli!

Wartości maksymalne wyliczamy ze wzorów:

1. dla tablicy kwadratowej:

C_max =
, gdzie k = liczba kolumn = liczba wierszu

2. dla tablicy prostokątnej:

C_max =

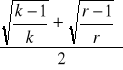
gdzie k = liczba kolumn

r = liczba wierszu

wartość skorygowaną C Pearsona obliczamy ze wzoru:

C kor =

ZADANIA:

1. Poniżej dana jest tabela przedstawiająca wyniki eksperymentu, którego celem było sprawdzenie czy uczniowie pochodzący z miasta i wsi różnią się pod względem postaw wobec legalizacji marihuany. Postawa wobec legalizacji marihuany mierzona była na skali dwuwartościowej, uczniowie mogli odpowiadać tylko: (1) jestem za legalizacją lub (2) nie jestem za legalizacją.

Wyniki wyglądają następująco:

	ZA	PRZECIW
WIEŚ	36	12
MIASTO	14	15

Polecenia:

1. sprawdzić czy stosunek młodzieży do kwestii legalizacji marihuany jest zależny do miejsca zamieszkania?

2. jeśli zależność okaże się istotna statystycznie, proszę sprawdzić jaka jest siła związku pomiędzy zmiennymi w tabeli

2. W roku 1962 zbadano czy ilość wypijanej Coca-Coli wpływa na trafność rozpoznawania jej smaku (eksperyment polegał na tym, że badanych zakwalifikowano do trzech grup ze względu na ilość wypijanej Coca-Coli: dużo, średnio i mało, a następnie w każdej grupie przeprowadzono tzw. ślepe testy - czyli badani nie wiedząc, jaki piją napój musieli zgadywać czy jest to Coca-Cola, Pepsi-Cola czy royal Crown; zakładano, że dużej ilości wypijanej Coca-Coli będzie towarzyszyła większa trafność w rozpoznawaniu jej smaku). Wyniki eksperymentu zamieszczam w tabeli poniżej.

		rozpoznawalność/ trafność
				niska	średnia	wysoka
SPOŻYCIE	DUŻE	10	14	16
		ŚREDNIE	7	9	10
		MAŁE	8	12	6

Polecenia:

1. sprawdzić czy wysokiemu spożyciu Coca-Coli towarzyszy większa rozpoznawalność jej smaku?

2. jeśli zależność okaże się istotna statystycznie, proszę sprawdzić jaka jest siła związku pomiędzy zmiennymi w tabeli

str. 1

---