#10 i 11 Analiza liczebności
chi-kwadrat

STATYSTYKA - ĆWICZENIA

Prowadzący: Rafał Styła
([e-mail])

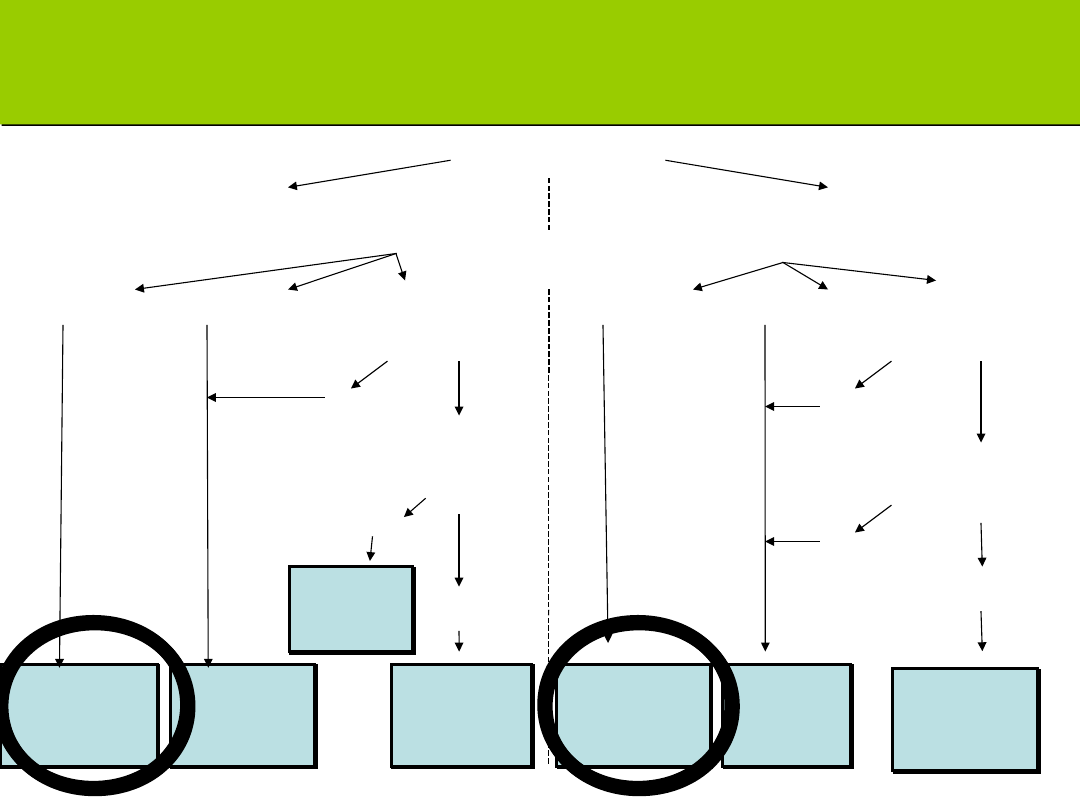
Ile grup
porównujemy?

dwie

więcej niż dwie

Na jakiej skali zmienna
zależna?

nominalna porządkowa

ilościowa

Chi-
kwadrat

U-Manna-
Whitneya

t-
Studenta

Jaki test wybrać, kiedy sprawdzamy istnienie różnic między
zmiennymi niezależnymi?

Rozkład
normalny?

tak

nie

Wariancje
homogeniczne?

nie

tak

Cochran
i Cox

nominalna porządkowa

ilościowa

Kruskala-
Wallisa

Rozkład
normalny?

nie

tak

nie

tak

F-
Fischera
(analiza
wariancji)

Źródło: Brzeziński J. (2004). Metodologia badań psychologicznych. Warszawa: Wydawnictwo Naukowe PWN.

Chi-
kwadrat

Wariancje
homogeniczne?

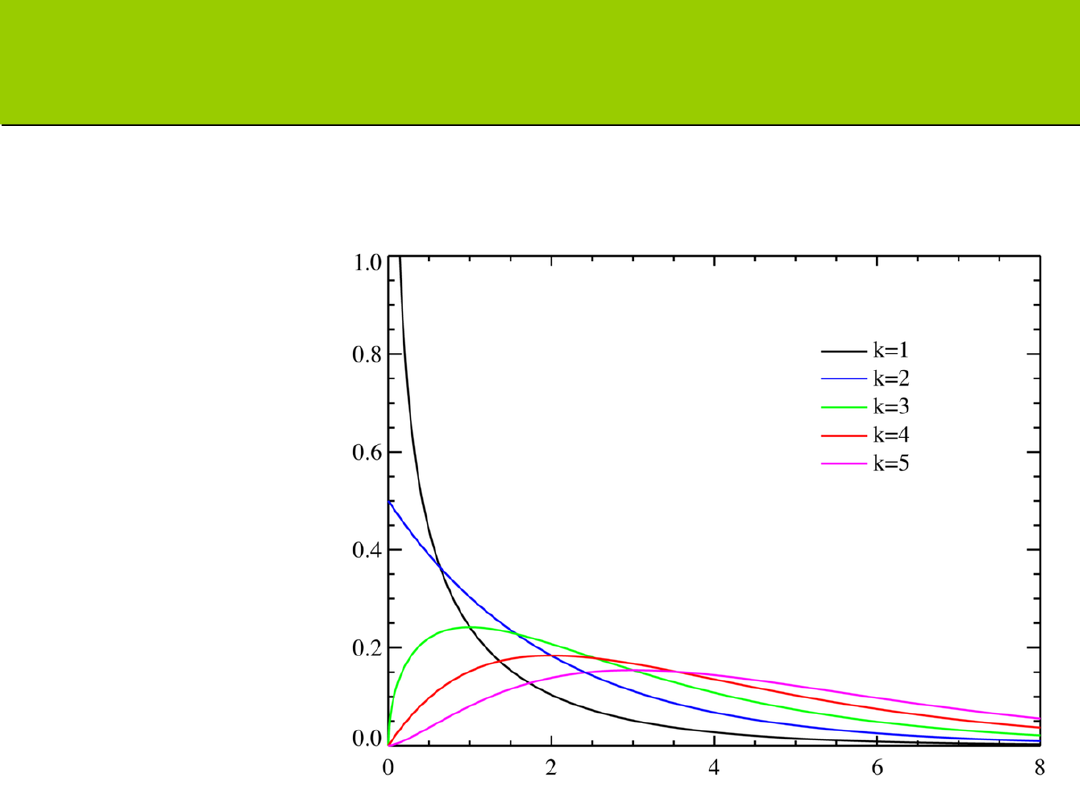
Rozkład chi-kwadrat



Model teoretyczny jak rozkład t. Stanowi rodzinę rozkładów
(różny przebieg dla różnej liczby stopni swobody).

Do czego służy rozkład chi-kwadrat?



Rozkład chi-kwadrat służy do sprawdzenia, czy dany
obserwowane wyniki, różnią się istotnie, bądź nie, od
danego rozkładu teoretycznego (oczekiwanego).



Np. 100 rzutów monety, a oczekiwanie, że moneta jest
rzetelna, czyli reszka i orzeł będzie równoliczny.



Badanie reprezentatywności próby z populacją.



Są dwie podstawowe grupy wykorzystania test chi-kwadrat:



Test zgodności i test niezależności

Test zgodności



Służy do tego, aby sprawdzić, czy uzyskany rozkład
wyników jest zgodny z rozkładem oczekiwanym



Np. 100 rzutów monety, a oczekiwanie, że moneta jest
rzetelna, czyli reszka i orzeł będzie równoliczny.



Np. Badanie reprezentatywności próby z populacją, czyli
sprawdzamy, czy w danej próbie rozkład zmiennych
nominalnych takich jak płeć czy zawód jest w takiej samej
proporcji, co w populacji



Stopnie swobody



Ilość możliwych kategorii-1



Np. Rzut kostką do gry, 6 kategorii-1 oznacza, że df=5

Obliczanie chi-kwadrat

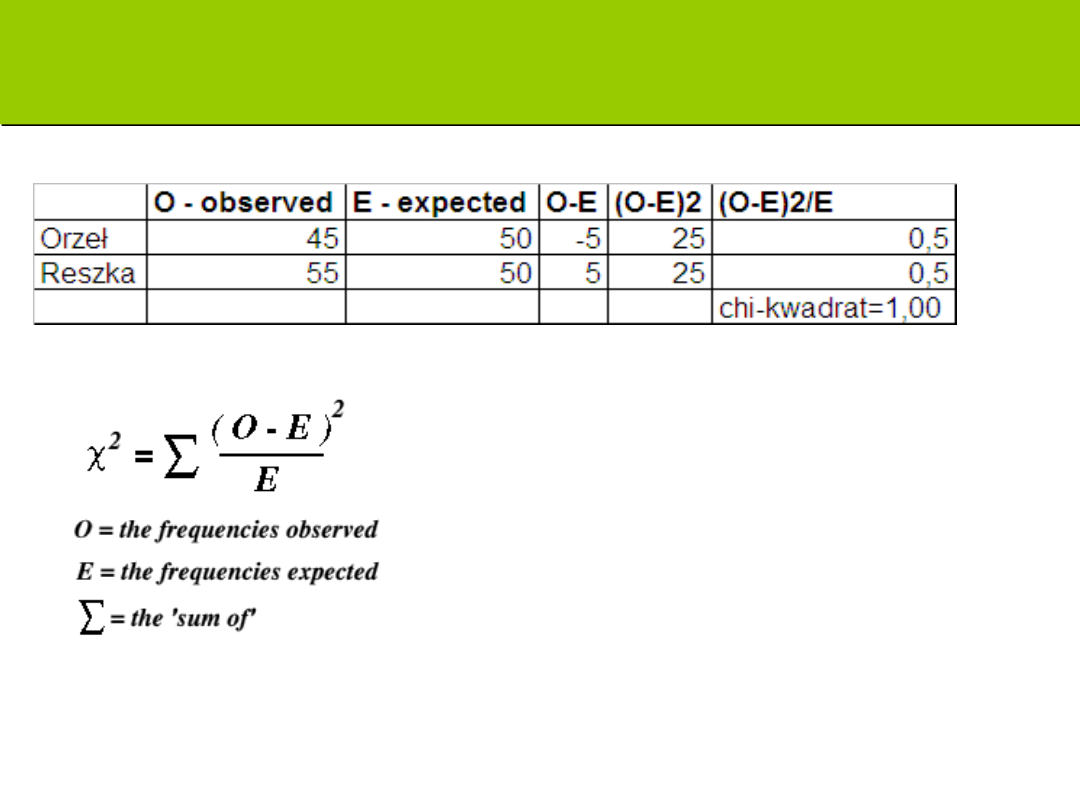
Zadanie: czy moneta jest rzetelna?

Jaki wniosek płynie z uzyskanej wartości testu:
POWTÓRZENIE

Podana reguła podejmowania decyzji jest stosowana do każdego z

testów statystycznych:

1.

Jeśli wartość uzyskana testu jest mniejsza niż wartość krytyczna z

tabeli rozkładu dla alfa=0,05 (np. chi-kwadrat, rozkład t) to

uznajemy, że różnice są nieistotne statystycznie i zapisujemy to

np. jako: chi

2

(1, N=50)=1; p>0,05.

2.

Jeśli wartość uzyskana testu jest większa niż wartość krytyczna z

tabeli rozkładu dla alfa=0,05, ale mniejsza od wartości krytycznej

dla alfa=0,01, to uznajemy, że istnieją statystycznie istotne

różnice i zapisujemy to np. jako: chi

2

(1, N=50)=5; p<0,05.

3.

Jeśli wartość uzyskana testu jest większa niż wartość krytyczna z

tabeli rozkładu dla alfa=0,01, ale mniejsza od wartości krytycznej

dla alfa=0,001, to uznajemy, że istnieją statystycznie istotne

różnice i zapisujemy to np. jako: chi

2

(1, N=50)=7; p<0,01.

4.

Jeśli wartość uzyskana testu jest większa niż wartość krytyczna z

tabeli rozkładu dla alfa=0,001, to uznajemy, że istnieją

statystycznie istotne różnice i zapisujemy to np. jako:

chi

2

(1, N=50)=12; p<0,001.

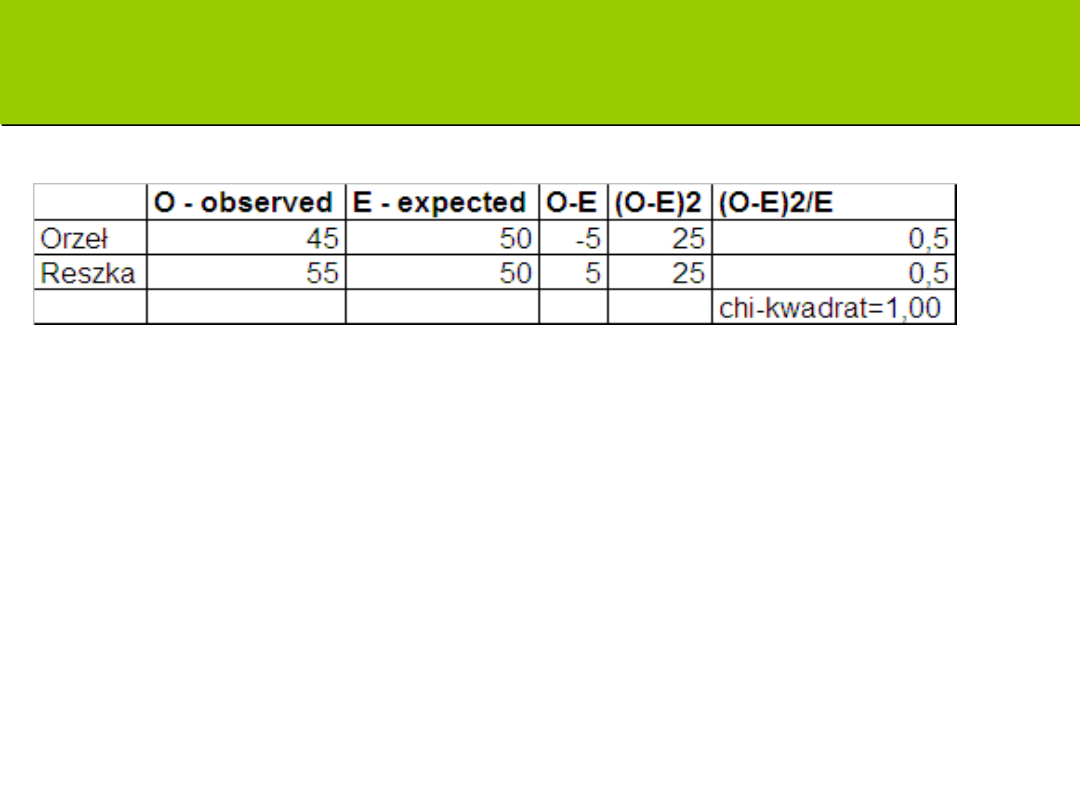
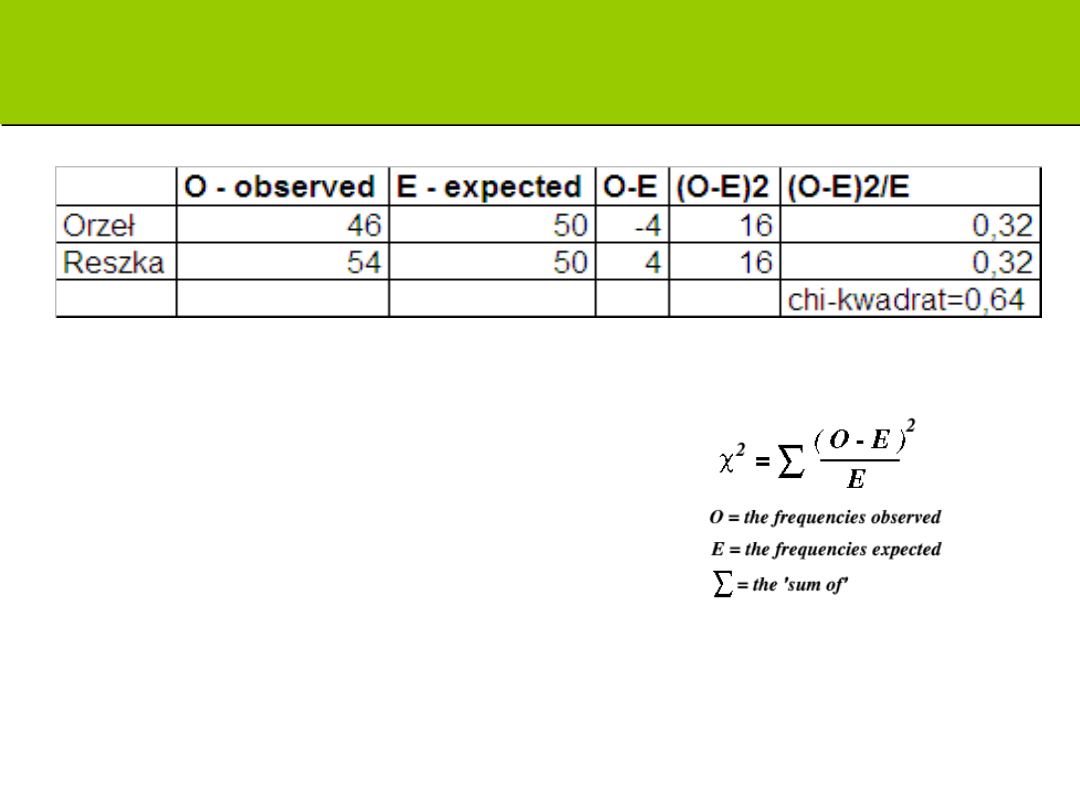
Zadanie: czy moneta jest rzetelna?

Zapis uzyskanego wyniku:

Aby sprawdzić, czy moneta jest rzetelna, przeprowadzono

analizę testem . Przeprowadzona analiza wykazała,
że uzyskany rozkład rzutów nie różni się istotnie od
rozkładu oczekiwanego dla rzetelnych monet (jest z nim
zgodny), (1, N=100)=1; p>0,05. Moneta jest
rzetelna.

2



2



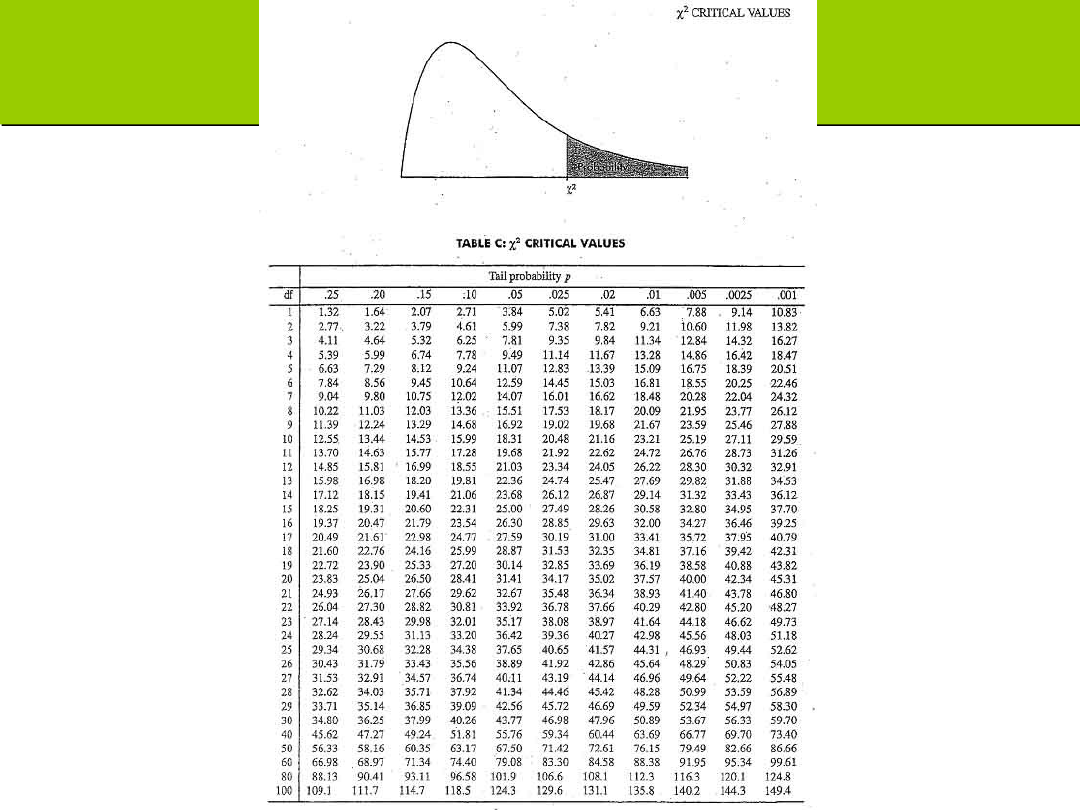
Zadanie: czy moneta jest rzetelna?

Zadanie: czy moneta jest rzetelna?

Testy niezależności



Test niezależności umożliwia sprawdzenie, czy zmienne
nominalne są od siebie niezależne (brak związku), czy też
są ze sobą związane



Stopnie swobody



Df= (kategorii w rzędzie-1)(kategorie w kolumnach-1), czyli
Df=(Rows-1)(Columns-1)



Np. sprawdzenie niezależności kategorii płeć (k i m) oraz koloru
włósów (czarne, brązowe, blond, inne)



Df=(2-1)(4-1)=1x3=3

Pytanie

Czy istnieje związek między

kolorem ubrania a płcią?

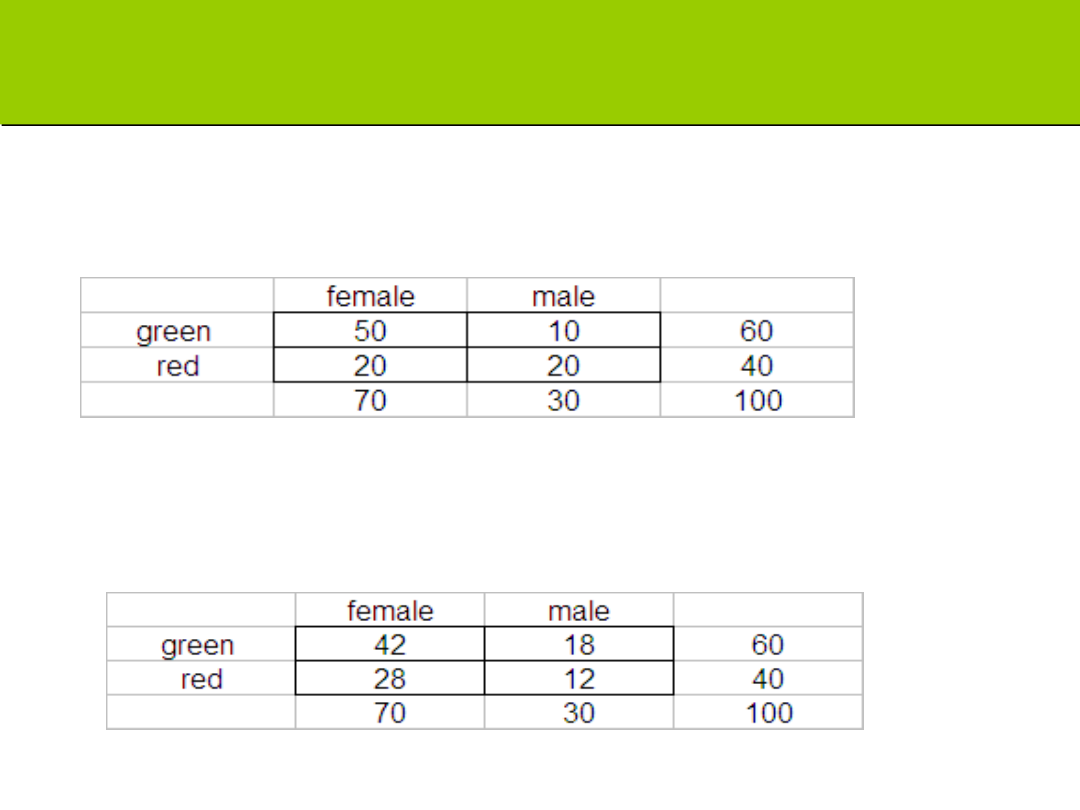
Tabele liczebności uzyskanych i
oczekiwanych



Wartości uzyskane



Wartości oczekiwane: mnożenie prawdopodobieństw



rządXkolumna/n = 60X70/100

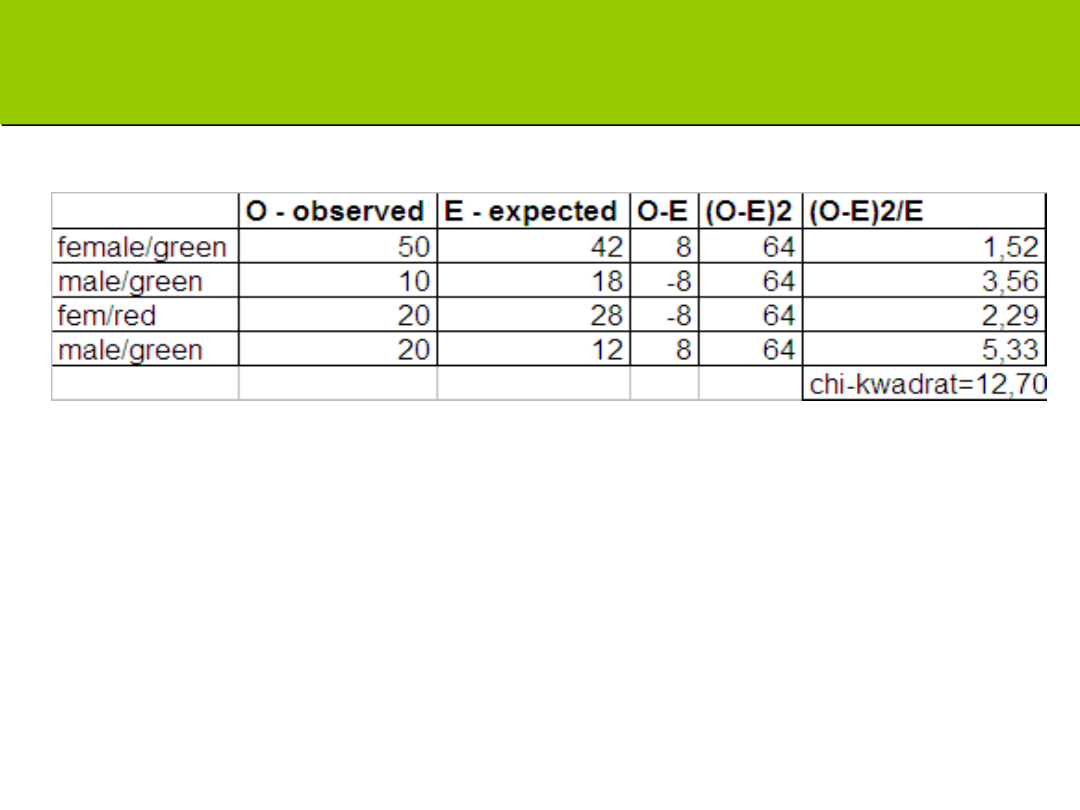
Gdy uzyskamy tabele liczebności oczekiwanych, dalej
obliczenia prowadzone są tak samo jak w przypadku
testu zgodności



Stopnie swobody



(Rows-1)(Columns-1)= (2-1)(2-1)=1



Wartość 12,7 przekracza wartość 10,83



Df=1, alfa=0,001



Mamy podstawę odrzucić hipotezę zerową o wzajemnej niezależności



Płeć i kolor ubrania nie są niezależne



Istnieje związek między płcią a kolorem ubrania

Zapis odpowiedzi

Aby sprawdzić, czy kolor noszonych ubrań jest zależny od płci,

przeprowadzono test chi-kwadrat. Przeprowadzona analiza
wykazała, że kolor ubrania jest zależny od płci, chi

2

(1,

N=100)=12,7; p<0,001. Kobiety chodzą częściej w
zielonym, a rzadziej w czerwonym od mężczyzn.

Praca domowa



1, 3, 5, 6, 7, 8, 9

Dziękuję za uwagę.