Wstęp teoretyczny 32

Cele ćwiczenia jest zbadanie właściwości fizycznych gazów, badane będą przemiany izobaryczne, izochoryczne oraz izotermiczne dla gazu.

Gaz - stan skupienia materii, w którym ciało fizyczne łatwo zmienia kształt i może zajmować całą dostępną mu przestrzeń.

Teoria kinetyczno-molekularna gazów wyjaśnia makroskopowe własności gazu na podstawie praw rządzących ruchem atomów, cząsteczek.

podstawowy wzór teorii kinetyczno-molekularnej gazów:

Nazwa ta bierze się stąd, że powyższy wzór wiąże parametry gazu: ciśnienie p oraz objętość V, a więc wielkości makroskopowe (mierzalne), z wielkościami mikroskopowymi: liczbą cząsteczek N i ich średnią energią kinetyczną E_K.
Na podstawie tego wzoru możemy powiedzieć, że:

Ciśnienie gazu w zbiorniku zamkniętym jest wprost proporcjonalne do liczby cząsteczek w naczyniu i średniej energii kinetycznej cząsteczek, a odwrotnie proporcjonalne do objętości naczynia.

Średnia energia kinetyczna gazu.
Jest to suma energii kinetycznych każdej z poszczególnych cząsteczek gazu podzielona przez liczbę cząsteczek. Średnią energię kinetyczną możemy również wyrazić poprzez wzór:

T - temperatura w stopniach Kelvina

k - stała Boltzmana, która zawsze wynosi

Ważnym jest, by temperatura była zawsze w stopniach Kelvina, jeżeli mamy podaną ją w stopniach Celsjusza, zamieniamy ją wg wzoru:

gdzie t - temperatura w stopniach Celsjusza.

Wzór na średnią energię kinetyczną mówi nam, że jeżeli w jakiejś przemianie obserwujemy wzrost temperatury gazu, oznacza to wzrost średniej energii kinetycznej jego cząsteczek, a więc wzrost średniej prędkości ruchu postępowego.
Oczywiście dociekliwi również na końcu paragrafu znajdą link do zagadnienia omawiającego wyprowadzenie wzoru na średnią energię kinetyczną.

Zauważcie, że dwa podane przeze mnie wzory: podstawowy wzór teorii kinetyczno-molekularnej gazów oraz wzór na średnią energię kinetyczną gazu, można połączyć:

Równanie stanu gazu doskonałego

doskonałego prawa Charlsa i Gay-Lusaca oraz avogadra wynika, że objętość gazu jest proporcjonalna odpowiednio do jego temperatury bezwzględnej i liczby moli. Prawo Boyle'a mówi, że objętość jest odwrotnie proporcjonalna do ciśnienia. Łącząc te 3 zależności otrzymujemy:
czyli

Stała proporcjonalności w zależności
oznaczana przez R nosi nazwę stałej gazowej:

pV=nRT

Jest to równanie stanu gazu doskonałego. Gaz, który w dowolnych warunkach stosuje się do tej zależności nazywa się gazem doskonałym. Wartość R można wyznaczyć mierząc p, V, n i T dla próbki gazu pod niskim ciśnieniem (zachowującego się wówczas jak gaz doskonały) i podstawiając odpowiednie wartości do wzoru
wyrażając ciśnienie w atmosferach, a objętość w litrach, otrzymuje się R= 0,08205781 l* atm/(K*mol). Równanie stanu gazu doskonałego obejmuje zależności opisujące reakcję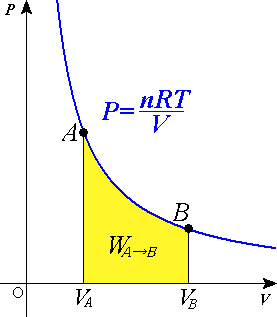
gazu doskonałego na zmiany ciśnienia, objętości, temperatury i liczby moli jego cząsteczek.

Prawo Boyle'a Mariotte'a

"W stałej temperaturze objętość V danej masy gazu jest odwrotnie proporcjonalna do jego ciśnienia p."

pV = const

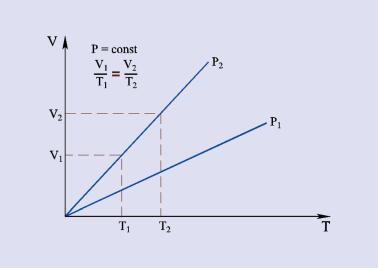
Prawo Charlesa

Pod stałym ciśnieniem objętość stałej ilości gazu zmienia się liniowo z temperaturą

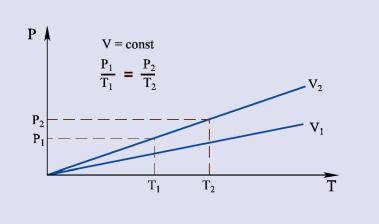
Przemiana izochoryczna

Prawo Gay-Lussaca

Objętość stałej masy gazy jest wprost proporcjonalna do temperatury w skali bezwzględnej

Dla dowolnej ilości moli gazu n w objętości V równanie van der Waalsa przybiera postać:

Równanie van der Waalsa stanowi na ogół bardzo dobre przybliżenie równania stanu gazów rzeczywistych, szczególnie dla dużych ciśnień i w temperaturach i ciśnieniu zbliżonych do parametrów skraplania gazu i powyżej.

Jeśli można zaniedbać oddziaływanie między cząsteczkami (a=0) i rozmiary samych cząsteczek (b=0) czyli traktować gaz jako gaz doskonały, to równanie van der Waalsa przechodzi w równanie Clapeyrona. Bardziej ogólnym równaniem opisujacym gazy rzeczywiste jest wirialne równanie stanu gazu.

---