Zastosowanie Matematyki w Finansach i Bankowości

1. W. Ronka-Chmielowiec, K. Kuziak: Podstawy matematyki finansowej. Wydawnictwo AE Wrocław, 2001.

2. E. Smaga: Arytmetyka Finansowa. Wydawnictwo Naukowe PWN, Warszawa-Kraków, 1999.

3. E. Smaga, E. Dobija: Podstawy matematyki finansowej i ubezpieczeniowej. Wydawnictwo Naukowe PWN, Warszawa-Kraków, 1995.

4. M. Sobczyk: Matematyka finansowa. Podstawy teoretyczne, przykłady, zadania. Agencja Wydawnicza PLACET, Warszawa 1995.

5. W. Bijak, M. Podgórska, J. Utkin: Matematyka finansowa. Teoria i praktyka obliczeń finansowych. Wydawnictwo Biznat, Warszawa 1994.

6. P. Chrzan: Matematyka finansowa. Podstawy Teorii procentu. Wyd. GigaNet sp. z o.o., Katowice 1998.

„Pieniądz otrzymany dzisiaj jest wart więcej, niż pieniądz otrzymany jutro”

zmienna wartość pieniądza w czasie

1. Spadek siły nabywczej.

2. Możliwość inwestowania.

3. Występowanie ryzyka.

4. Preferowanie bieżącej konsumpcji przez człowieka.

Wartość pieniądza w czasie odzwierciedlana jest przez stopę procentową

Stopa procentowa - cena, jaką pożyczkobiorca musi płacić za przywilej korzystania z pieniędzy udostępnionych mu przez pożyczkodawcę, a pożyczkodawca jest wynagradzany za to, że nie dysponuje swoimi pieniędzmi

• Stopa procentowa w skali okresu (najczęściej w skali roku)

• Stopa procentowa dotycząca okresu (np. półroczna oznaczająca okres działalności inwestycyjnej)

Aktualizacja wartości kapitału może dotyczyć momentu 0 lub pewnego momentu w przyszłości

Operacje:

1) Kapitalizacja jest operacją polegającą na obliczaniu kwoty, do jakiej wzrasta po określonym czasie wpłacony kapitał (inaczej dopisywanie odsetek do kapitału)

Kapitalizacja i reinwestycja

dochody pojawiające się w okresie inwestowania są kapitalizowane („dodawane do kapitału”), w efekcie czego występuje zjawisko reinwestowania (ponownego inwestowania dochodów z inwestycji)

2) Dyskontowanie jest operacją otrzymywania wartości początkowej kapitału na podstawie przyszłej wartości kapitału.

• Stopa procentowa występująca przy kapitalizacji mierzy tempo pomnażania wartości kapitału w czasie

• Stopa procentowa występująca przy dyskontowaniu mierzy tempo pomniejszania wartości kapitału w czasie

W praktyce stopy te mogą być różne.

• wartość przyszła pieniądza (FV) - wartość otrzymywana lub płacona w przyszłości;

kwota pieniężna, którą uzyskuje się w przyszłym okresie po zastosowaniu kapitalizacji do kwoty początkowej

• wartość bieżąca pieniądza, wartość obecna, wartość teraźniejsza, wartość aktualna, wartość zaktualizowana, wartość zdyskontowana, wartość dzisiejsza (PV) - wartość otrzymywana lub płacona dziś;

wartość pieniądza w chwili obecnej

Aby dokonać kapitalizacji i dyskontowania trzeba określić stopę procentową i czas.

okres stopy procentowej - bazowa jednostka czasu, po której kapitał początkowy wzrasta o odpowiedni procent

stopa procentowa - procent, o jaki wzrasta kapitał po upływie bazowej jednostki czasu (taką jednostką jest zazwyczaj rok)

r =

Stopa procentowa:

• liczba niemianowana

• przyjmuje wartości na ogół z przedziału (0,1)

• można ją wyrazić w procentach, mnożąc przez 100%

Okres konwersji - przedział czasu, w którym oblicza się oprocentowanie. Okres bazowy jest zbieżny z okresem konwersji, lub jest jego wielokrotnością

Jeśli odsetki dopisywane są:

• na końcu okresu, kapitalizacja z dołu

• na początku okresu, kapitalizacja z góry

schematy przepływów pieniężnych:

• pojedynczy przepływ pieniężny

• renta płatna z dołu

• renta płatna z góry

• wiele regularnych przepływów pieniężnych

pojedynczy przepływ pieniężny

Model kapitalizacji prostej z dołu

Jeżeli odsetki od kapitału powiększają stan konta, ale nie podlegają oprocentowaniu po upływie kolejnej bazowej jednostki czasu, nie są one kapitalizowane, to mówimy, że jest to kapitalizacja prosta.

Kapitał początkowy PV po upływie jednej jednostki czasu wynosi:

FV₁ = PV + PV r = PV (1 + r),

Po upływie dwóch jednostek czasu:

FV₂ = PV + PV r + PV r = PV (1 + 2r),

Po upływie n jednostek czasu :

FV_n = FV_n-1 + PV r = PV (1 + nr),

FV = PV (1 + nr)

Pozostałe wzory

PV =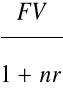

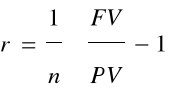
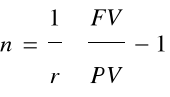
Czas podwojenia kapitału dla kapitalizacji prostej

2 PV = PV (1 + n r )

2 = 1 + n r

n = 1/r

Model kapitalizacji złożonej zgodnej z dołu

Jeśli oprocentowaniu podlega kapitał początkowy powiększony o nagromadzone odsetki, to mówimy, że jest to kapitalizacja złożona.

Zakładamy, że okres konwersji i bazowa jednostka czasu są identyczne (kapitalizacja zgodna), odsetki dopisywane są na końcu okresu.

Po roku kapitał PV wzrasta do kwoty FV₁:

FV₁ = PV + PV r = PV (1 + r).

Po dwóch latach kapitał wzrasta do kwoty FV₂:

FV₂ = FV₁ +FV₁ r = FV₁ (1 + r) = PV (1 + r)².

Po n latach kapitał wzrośnie do kwoty FV_n:

FV_n = PV (1 + r)ⁿ

FV - PV = PV ((1 + r)ⁿ - 1)

Kwotę tę nazywamy zarobionymi odsetkami

Pozostałe wzory

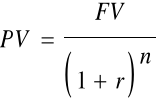
v =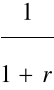
PV = FV vⁿ

r =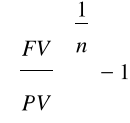
v =

n =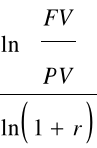

Czas podwojenia kapitału dla kapitalizacji złożonej z dołu

n =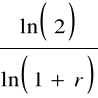

n =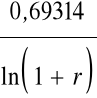

Rys. Czas podwojenia kapitału dla kapitalizacji złożonej

Model kapitalizacji złożonej zgodnej z góry

FV₁ =PV + PV r + PV r² + PV r³ +...

= PV (1+ r + r² +... ) =

= PV
= PV (1 - r)^-1,

warunek zbieżności szeregu r < 1

Wartość przyszła kapitału FV_n+1 przy wykorzystaniu wartości kapitału FV_n:

FV_n+1 = FV_n + FV_n r + FV_n r² + FV_n r³ +... =

=FV_n (1 + r + r² + r³ +... ) =

=FV_n
= FV_n (1 - r )^-1,

warunek zbieżności szeregu r < 1

Ciąg FV_n jest ciągiem geometrycznym o pierwszym wyrazie FV₁ i ilorazie (1 - r)^-1:

FV_n = FV₁ [(1 - r)^-1]^n-1

= PV (1 - r)^-1 [(1 - r)^-1]^n-1 =

= PV (1 - r)^-n,

n = 1, 2,...

FV_n = PV (1 - r)^-n

Kapitalizacja odsetek w podokresach okresu bazowego oprocentowania

W tym przypadku okres bazowy jest wielokrotnością okresu konwersji i stopa efektywna jest różna od stopy nominalnej.

Niech r^(m) oznacza nominalną roczną stopę procentową. Oznacza to, że rok jest podzielony na m okresów procentowych równych co do długości. Po każdym m-okresie procentowym występuje kapitalizacja odsetek.

Po 1/m roku kapitał powiększy się do wielkości

FV_1/m = PV + PV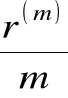
= PV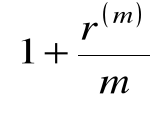

Po 2/m roku kapitał powiększy się do wielkości

FV_2/m = FV_1/m + FV_1/m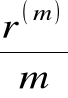
= PV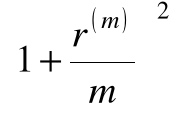

Po k/m roku kapitał powiększy się do wielkości

FV_k/m = PV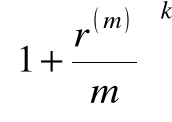
.

Po upływie pierwszego roku kapitał powiększy się do wielkości

FV₁ = PV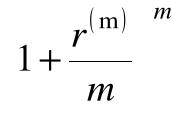

Jeżeli kapitał ulokujemy na koncie na n lat i poddamy kapitalizacji złożonej, gdzie m jest liczbą podokresów procentowych w każdym roku, to kapitał wzrośnie po n latach do wielkości:

FV_n = PV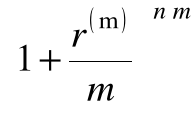

Pozostałe wzory

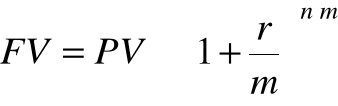
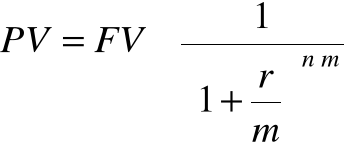
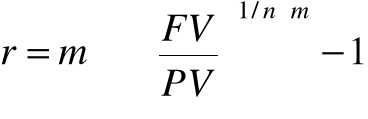
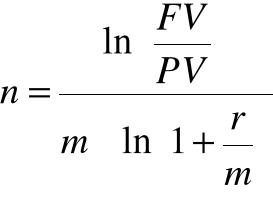
Model kapitalizacji ciągłej

W przypadku, gdy momentów kapitalizacji w bazowej jednostce czasu będzie coraz więcej, czyli kapitalizacja będzie się odbywała coraz częściej, to w przypadku granicznym otrzymamy kapitalizację ciągłą.

m →

dla n = 1

,

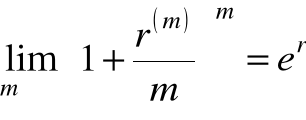
e = 2,718....

Przy ciągłej kapitalizacji odsetek stan konta w każdym momencie t oblicza się ze wzoru:

F(t) = F(0) e^rt

Po n okresach

FV_n = PV e^rn

Pozostałe wzory

PV = FV_n e^-rn

r =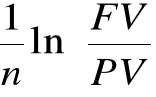

n =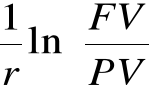

Można znaleźć również efektywną stopę procentową dla kapitalizacji ciągłej

r_ef = e^r - 1

Zarobione odsetki w okresie o długości n stanowią wielkość

FV - PV

Przykład

Kapitał w wysokości 1000 jednostek złożono na koncie z nominalną roczną stopą procentową 10%. Do jakiej wielkości wzrośnie stan konta po 10 latach?

• kapitalizacja odsetek codzienna m = 360,

FV = 1000 (1,00027777)³⁶⁰⁰ = 2717,9036.

• kapitalizacja odsetek miesięczna

m =12,

FV = 1000 (1,0083333)¹²⁰ = 2707,0414.

• kapitalizacja odsetek kwartalna

m = 4,

FV = 1000 (1,025)⁴⁰ = 2685,0638.

• kapitalizacja odsetek półroczna

m = 2,

FV = 1000 (1,05)²⁰ = 2653,2977.

• kapitalizacja odsetek roczna

m = 1,

FV = 1000 (1,1)¹⁰ = 2593,742

19

dyskontowanie

kapitalizacja

PV

FV

n

2

1

0

pożyczka

inwestycjaaa

n

20

15

10

5

0,05 0,06 0,07 0,08 0,09 0,1 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,2 r

0,05 0,06 0,07 0,08 0,09 0,1 0,11 0,12 0,13 0,14 0,15 r

5

10

15

20

n

---