Rozwiązania wybranych zadań z teorii względności
Zad.1. Rakieta porusza się z szybkością v = 0,8 c. Obserwator na Ziemi zmierzył czas trwania pewnego zjawiska na Ziemi i otrzymał wynik 800 s. Jak długo trwało to zjawisko wg pilota rakiety?
Dane: Szukane:
v = 0,8 c t = ?
to = 800 s
Obserwator na Ziemi zmierzył czas własny zjawiska, stąd oznaczenie to.
Wg pilota rakiety zjawisko trwało dłużej:
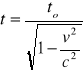
Stąd
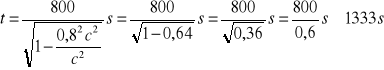
Odp.: Wg pilota rakiety zjawisko trwało około 1333 s.
Zad.2. Rakieta porusza się z szybkością v = 0,8 c. Obserwator na Ziemi zmierzył czas trwania pewnego zjawiska w rakiecie otrzymał wynik 800 s. Jak długo trwało to zjawisko wg pilota rakiety?
Dane: Szukane:
v = 0,8 c t = ?
t = 800 s
Obserwator na Ziemi zmierzył czas relatywistyczny zjawiska, stąd oznaczenie t.
Wg pilota rakiety zjawisko trwało krócej, bo mierzy on czas własny trwania tego zjawiska:
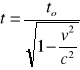
Przekształcamy wzór i otrzymujemy 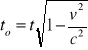
Stąd
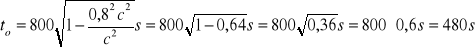
Odp.: Wg pilota rakiety zjawisko będzie trwało 480 s.
Zad.3. Rakieta porusza się z szybkością v = 0,6 c. Pilot zmierzył długość swojej rakiety i uzyskał wynik 120 m. Oblicz, jaki wynik tego samego pomiaru otrzyma obserwator na Ziemi?
Dane: Szukane:
v = 0,6 c l = ?
lo = 120
Pilot rakiety zmierzył długość własną lo rakiety, zaś obserwator na Ziemi zmierzy długość relatywistyczną l rakiety.
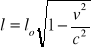
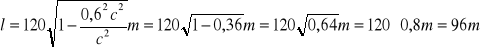
Odp.: Obserwator na Ziemi stwierdzi, że rakieta ma długość 96 m.
Zad.4. Dwie rakiety poruszają się „na czołówkę”. Obserwator zmierzył ich szybkości i uzyskał wyniki v1=0,6c oraz v2=0,8c. Oblicz, z jaką szybkością zbliżają się te rakiety wg obserwatora z Ziemi a z jaką wg pilotów rakiet.
Dane: Szukane:
v1 = 0,6 c vz = ?
v2 = 0,8 c vp = ?
Załóżmy, że obie rakiety lecą tak, że widzimy je prostopadle i w pewnej chwili możemy przyjąć, że od nas się nie oddalają ani się do nas nie zbliżają.
Zmierzona przez nas ich szybkość względna wyniesie:
![]()
![]()
Uzyskana szybkość 1,4 c nie jest niczym dziwnym, przecież to nie jest szybkość mierzona względem nas.
Wg każdego z pilotów rakiet szybkość względną obliczymy ze wzoru:
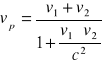
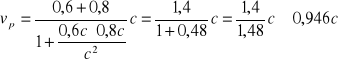
Jak widać, piloci rakiet zmierzą swoją względną szybkość jako mniejszą od c!
Odp.: Według obserwatora z Ziemi rakiety zbliżają się z szybkością 1,4 c a wg pilotów z szybkością około 0,946 c.
Zad.5. Czas życia w laboratorium pewnych cząstek wynosi 5 ms. Jaki będzie ich czas życia po przyspieszeniu w akceleratorze do szybkości 0,99 c.
Dane: Szukane:
v = 0,99 c t = ?
to = 5 ms
W laboratorium zmierzono czas własny zjawiska, stąd oznaczenie to.
Po przyspieszeniu do szybkości relatywistycznych czas życia wzrośnie:
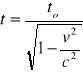
Stąd
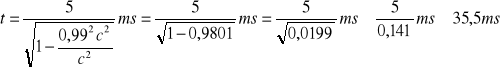
Odp.: Po przyspieszeniu cząstek ich czas życia wzrośnie do około 35,5 ms.
Zad.6. Oblicz, jak długo świeciłaby żarówka o mocy 100 W, jeśli źródłem jej energii byłaby anihilacja 1 kg materii i 1 kg antymaterii?
Dane: Szukane:
P = 100 W t = ?
m = 1 kg + 1 kg = 2 kg
c = 3·108 m/s
Obliczmy, ile energii uzyskamy z anihilacji 2 kg masy ze wzoru (sprawdź jednostkę):
E = m·c2
![]()
Energia ta zostanie zużyta na pracę prądu elektrycznego przepływającego przez żarówkę:
E = W = P·t
stąd
![]()
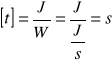
![]()
Jest to bardzo duża liczba. Np. rok ma około 32 miliony sekund (3,2·107 s). Żarówka świeciłaby tą energią około 50 milionów lat.
Odp.: Żarówka świeciłaby tą energią około 50 milionów lat.
Zad.7. Znajdź zależność gęstości ciała od jego szybkości zgodną z teorią relatywistyczną. Dla ułatwienia przyjmij, że ciało ma kształt prostopadłościanu i porusza się w kierunku równoległym do jednej z jego krawędzi. Oblicz, o ile % zmieni się gęstość ciała, jeżeli nadano mu prędkość 0,8c.
Dane: Szukane:
v = 0,8 c ![]()
Gęstość spoczynkowa (własna) wyraża się wzorem: ![]()
Gęstość relatywistyczna ![]()
Masa relatywistyczna 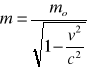
Objętość relatywistyczna - przy założeniu, że ruch zachodzi wzdłuż boku c:
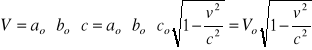
Ostatecznie gęstość relatywistyczna:
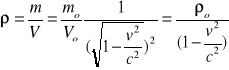
Przy szybkości v = 0,8 c gęstość ciała rośnie:
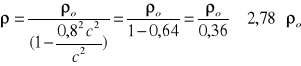
Zmiana gęstości wynosi: ![]()
Względna zmiana gęstości: ![]()
Odp.: Przy szybkości 0,8 c gęstość ciała wzrasta o około 178 %.
Zad.9. Z Ziemi wysłano impuls świetlny w kierunku Księżyca. W sekundę po tym zdarzeniu na powierzchni Księżyca zaobserwowano błysk światła. a) Czy może istnieć związek przyczynowy między tymi zdarzeniami? b) Czy istnieje taki układ inercjalny, w którym wysłanie impulsu świetlnego z Ziemi nastąpiłoby w tej samej chwili, co błysk światła na powierzchni Księżyca? Odległość Księżyca od Ziemi wynosi 3,84·108 m.
Odp. a) NIE może istnieć związek przyczynowy między tymi zdarzeniami, bo impuls świetlny w czasie 1 sekundy nie doleciał do Księżyca (384 000 km > 300 000 km).
Odp. b) TAK, istnieje wiele takich układów odniesienia. Wystarczy, aby w sekundę od wysłania z Ziemi impulsu układ taki znalazł się w odległości x = (300 000 + 84 000/2) km = 342 000 km od Ziemi.
Zad.10. Przy jakiej szybkości elektron podwoi swoją masę spoczynkową? Jaka jest całkowita energia elektronu dla tej prędkości? Podobne rozważania przeprowadzić dla protonu.
Dane: Szukane:
m = 2 mo v = ?
![]()
Ee = ?
![]()
Ep = ?
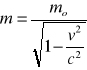
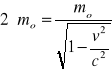
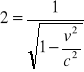
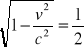
![]()
![]()
![]()
Ostatecznie ![]()
Energię całkowitą dowolnej masy obliczamy ze wzoru: E = m·c2
Dla elektronu: ![]()
Dla protonu: ![]()
Odp.: Elektron podwoi swoja masę przy szybkości około 87% szybkości światła. Energie całkowite wyniosą wtedy odpowiednio![]()
oraz ![]()
Wyszukiwarka
Podobne podstrony:
Metodyka rozwiązywania zadań, Transport Politechnika, Semestr 1, Fizyka
zestaw-zadan-1, Fizyka liceum - rozszerzona
Ruch jednostajnie przyspieszony - rozwiązywanie zadań, Studia, Semestr 1, Fizyka, Sprawozdania
pole grawitacyjne zadanie rozwiazane, fizyka, liceum
Metodyka rozwiązywania zadań, Transport Politechnika, Semestr 1, Fizyka
rozwiazywanie zadan tekstowych wb
efekt plejotropowy rozwiazanie zadań 1
cw8s rozwiazania zadan new id 123854
Rozwiązania zadań sprawdzających EKONOMIA działy 1-4, UP, ekonomia
Octan izoamylu rozwiązanie zadań
dodawanie rozwiazywanie zadań
38 Olimpiada Wiedzy Technicznej I Stopień Rozwiązania Zadań
Logika rozwiazania zadan id 272023
GM P1 142 Rozwiazania zadan i s Nieznany
CIĄGI – rozwiązanie zadań
więcej podobnych podstron