Wydział Mechaniczny Rok I semestr II Gr. Lb 1 |
Temat : Pomiar pojemności kondensatora metodą mostka Wheatstone'a. |
07.05.2013 |
Ćw. nr 19 |
Kamil Kosut |
|
Wstęp
Przy pomocy urządzenia nazywanego mostkiem wheatstone'a możemy
zbadać nieznane pojemności kondensatorów. W doświadczeniu szukamy
pojemności kondensatorów ![]()
![]()
. Znajdujemy je poprzez dobranie
odpowiedniej wartości kondensatora dekadowego tak, aby natężenie
dźwięku w słuchawkach było jak najmniejsze . Natężenie dźwięku osiągało
wartości minimalne , gdy prąd nie płynął . Wtedy pomiędzy punktem e i d nie
ma różnicy potencjałów . Wówczas:
![]()
![]()
Oznaczając prądy odpowiednio:
![]()
![]()
![]()
prąd na odcinku ADB
![]()
![]()
![]()
-prąd na odcinku AEB
![]()
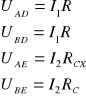
Ze względu na równość odpowiednich napięć , po podstawieniu
otrzymujemy :
![]()
![]()
Z ![]()
tej równości wynika , że: ![]()
Doprowadzenie napięcia do okładzin kondensatora powoduje zgromadzenie się na nich ładunku elektrycznego. Jeżeli kondensator jako całość nie jest naelektryzowany, to cały ładunek zgromadzony na jego okładkach jest jednakowy, ale przeciwnego znaku. Kondensator charakteryzuje pojemność określająca zdolność kondensatora do gromadzenia ładunku:
gdzie:
C - pojemność, w faradach
Q - ładunek zgromadzony na jednej okładce, w kulombach
U - napięcie elektryczne między okładkami, w woltach.
Pojemność wyrażana jest w faradach. Jeden farad to bardzo duża jednostka, dlatego w praktyce spotyka się kondensatory o pojemnościach piko-, nano-, mikro- i milifaradów.
Ogólnie, napięcie uC i prąd iC kondensatora w chwili t związane są zależnością:
Pracę dW, jaką trzeba wykonać by przenieść niewielki ładunek dq z jednej okładki kondensatora, o pojemności C, na drugą, przy założeniu, że jedna z okładek jest naładowana ładunkiem q.
Energię zmagazynowaną w kondensatorze oblicza się przez scałkowanie powyższego wzoru, uzyskując:
przy czym Q jest ładunkiem, do którego naładowano kondensator.
Prąd elektryczny to zmiana ładunku w czasie, co można zapisać:
Kondensator podłączony do napięcia stałego po pewnym czasie naładuje się do tego napięcia
kondensator jest wówczas równoważny przerwie w obwodzie (iC = 0). Dla prądu przemiennego przez kondensator płynie prąd określony wzorem:
Wielkość wiążąca prąd i napięcie na kondensatorze nazywa się reaktancją, która jest tym mniejsza, im większa jest pojemność kondensatora i częstotliwość prądu. Kondensator charakteryzuje się tym, że (dla sygnałów sinusoidalnych) napięcie jest opóźnione w fazie względem prądu o kąt 90 stopni (inaczej: prąd wyprzedza napięcie o kąt 90 stopni). Z tego względu impedancja kondensatora jest wartością urojoną i opisana jest wzorem:
,
Gdzie :ω to częstość, f to częstotliwość w hercach.
Układ pomiarowy
3.Tabele pomiarowe
Nr kondensatora |
Pomiar 1 C[nF] |
Pomiar 2 C[nF] |
Pomiar 3 C[nF] |
Pomiar 4 C[nF] |
Pomiar 5 C[nF] |
Wartość śr. C[nF] |
Błąd kondensatora ∆C |
C1 |
630 |
630 |
630 |
630 |
630 |
630 |
0 |
C2 |
990 |
990 |
990 |
990 |
1000 |
992 |
2 |
C3 |
93 |
92 |
93 |
92 |
92 |
92,4 |
0,25 |
C4 |
330 |
330 |
330 |
330 |
330 |
330 |
0 |
C5 |
2070 |
2100 |
2110 |
2100 |
2110 |
2098 |
7,35 |
Szeregowo C1 C2 |
385 |
385 |
383 |
383 |
384 |
384 |
0,78 |
Równolegle C1 C2 |
1600 |
1600 |
1600 |
1600 |
1600 |
1600 |
1,41 |
4.Błędy pomiarowe
Niepewność standardową u (Cx śr) obliczamy ze wzoru:
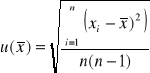
Dla kondensatora C1:
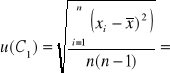
0
Dla kondensatora C2 :
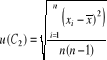
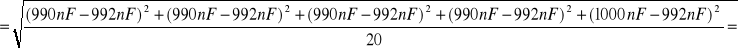
![]()
Dla kondensatora C3 :
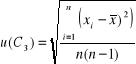
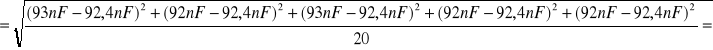
![]()
Dla kondensatora C4 :
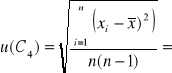
0
Dla kondensatora C5 :
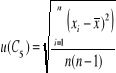
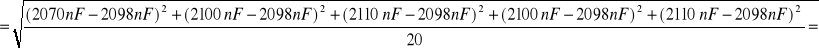
![]()
Pojemność zastępcza dla kondensatorów C1 i C2 połączonych szeregowo obliczamy ze wzoru:
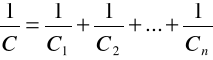
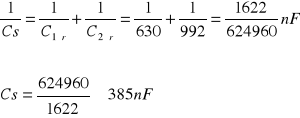
Pojemność zastępcza dla kondensatorów C1 i C2 połączonych równolegle obliczamy ze wzoru:
![]()
![]()
Niepewność złożona dla połączenia szeregowego :
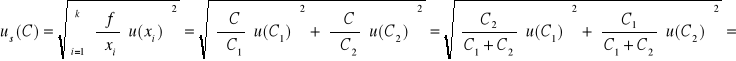
![]()
Niepewność złożona dla połączenia równoległego:
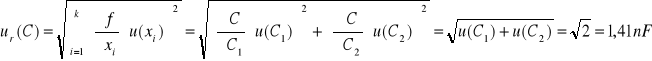
Zestawienie wyników:
Pojedyncze kondensatory:
![]()
![]()
![]()
![]()
![]()
Dla połączonych szeregowo:
![]()
Dla połączonych równolegle:
![]()
Porównanie danych w %:
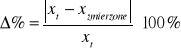
Dla połączenia równoległego:
CR: ![]()
Dla połączenia szeregowego:
CS: ![]()
5. Wnioski:
W wypadku takiego układu pomiarowego możemy wyznaczyć pojemność kondensatorów. Przy warunkach w jakich wykonywane było ćwiczenie polepszenie pomiaru można uzyskać przy przeprowadzeniu pomiarów w jak największej ciszy. Przy pomiarze baterii kondensatorów wyniki otrzymane bezpośrednio z pomiaru są bardzo zbliżone do obliczonych wyników.
Dokładność z jaką wyznaczyliśmy układy kondensatorów sugeruje iż z podobną dokładnością zostały wyznaczone pojemności poszczególnych kondensatorów.
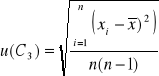
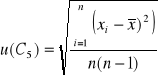
Wyszukiwarka
Podobne podstrony:
gamma dobree!!, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
Cwiczenie23, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
Bryła sztywna na równi pochyłej, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego2, Studia, laborki fizyka (opole
POMIAR POJEMNOŚCI KONDENSATORA METODA MOSTKA WHEATSTONE 'A, Studia, laborki fizyka (opole, pol
Sprawdzanie prawa Malusa, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
sprawozdanie z stała Plancka, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania 3
DIODA, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania 3
Badanie ruchu bryły sztywnej po równi pochyłej, Studia, laborki fizyka (opole, politechnika opolska)
Temat 24 Kondensator 1, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
termistor freier, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
gamma dobree!!, Studia, laborki fizyka (opole, politechnika opolska), Sprawozdania
mostek wheat, studia, semestr II, SEMESTR 2 PRZYDATNE (od Klaudii), Od Górskiego, II semestr, Fizyka
DŁAWIK, Politechnika Opolska, sprawozdania, Teoria obwodów
Elektronika - Przetwornice prądu stałego, Politechnika Opolska, sprawozdania, zachomikowane, Elektro
wskazowe, Politechnika Opolska, sprawozdania, zachomikowane, teoria obwodów
Elektronika - Układy próbkująco-pamiętające, Politechnika Opolska, sprawozdania, zachomikowane, Elek
Elektronika - Badanie cyfrowych bramek logicznych, Politechnika Opolska, sprawozdania, zachomikowane
Sprzężenia, Politechnika Opolska, sprawozdania, zachomikowane, Automatyka
więcej podobnych podstron