ĆWICZENIE 15

ELEKTRYCZNY MODEL KOMÓRKI

1. Prąd elektryczny (natężenie prądu, napięcie, opór, opór właściwy, prawo Ohma, prawa Kirchhoffa, obliczanie natężeń prądów płynących w oczkach obwodu).

Prąd elektryczny - uporządkowany (skierowany) ruch ładunków elektrycznych. W naturze przykładami są wyładowania atmosferyczne, wiatr słoneczny, czy czynność komórek nerwowych, którym również towarzyszy przepływ prądu. W technice obwody prądu elektrycznego są masowo wykorzystywane w elektrotechnice i elektronice. Prąd elektryczny jest w istocie ruchem cząstek obdarzonych ładunkiem, zwanych nośnikami ładunku. Umownie przyjęło się określać kierunek przepływu prądu poprzez opisanie ruchu ładunków dodatnich, niezależnie od tego jaki jest rzeczywisty znak i kierunek ruchu nośników w danym materiale. W metalach (zarówno stałych, jak i w stanie ciekłym) nośnikami ładunku są elektrony. Elektrony znajdujące się w paśmie przewodnictwa mogą swobodnie się przemieszczać w objętości metalu. Dlatego wszystkie metale są dobrymi przewodnikami, a prąd elektryczny w metalach jest ruchem elektronów przewodnictwa. W konwencjonalnych półprzewodnikach (takich jak krzem czy german) w temperaturze zera bezwzględnego nie ma elektronów w paśmie przewodnictwa. Przewodzenie prądu wymaga przeniesienia elektronów z pasma walencyjnego do przewodnictwa (poprzez dostarczenie im energii, na przykład termicznej lub w postaci promieniowania).W elektrolitach, zarówno ciekłych, jak i stałych nośnikami ładunku są ruchliwe jony - ujemne aniony i dodatnie kationy. W niektórych elektrolitach występują ruchliwe jony obu znaków, w innych tylko jednego. Istnieją przewodniki jonowe wykazujące bardzo dobre przewodnictwo elektryczne nawet w stanie stałym (przewodniki superjonowe).W gazach nośnikami prądu są jony, zarówno dodatnie jak i ujemne. W próżni i rozrzedzonych gazach można wytworzyć wolne elektrony, których ruch jest prądem elektrycznym.

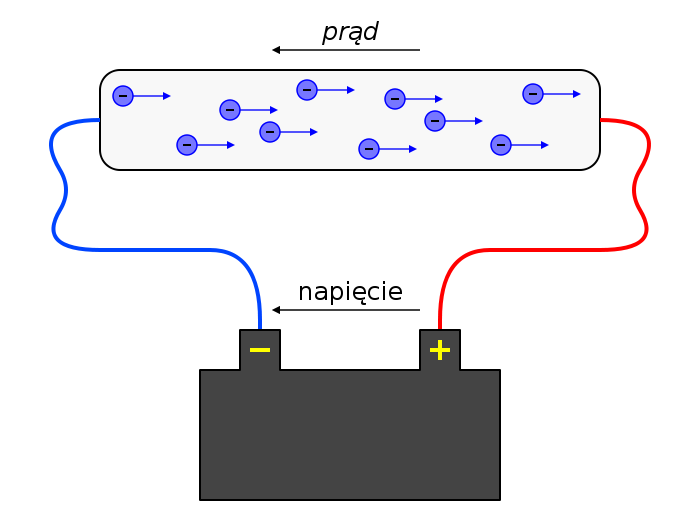
Przewodnictwem mieszanym określa się takie przewodnictwo, w którym występuje zarówno z przewodnictwo elektronowe, jak i jonowe. Tego typu przewodnictwo jest istotne na przykład w materiałach, z których wykonywane są elektrody ogniw paliwowych. W wielu przypadkach wygodny jest opis procesu przewodzenia za pomocą kwazicząstek. Czyni się tak w przypadku półprzewodników, gdzie ruch elektronów w paśmie walencyjnym opisuje się raczej za pomocą ruchu "pustego miejsca po elektronie", czyli dziury. Podobnie ruch elektronów w niektórych materiałach amorficznych i skompensowanych półprzewodnikach opisuje się za pomocą polaronów, czy nośniki ładunku w nadprzewodnikach za pomocą par Coopera. Ruch naładowanego ciała, jako całości jest również prądem elektrycznym. Podstawowymi parametrami nośników prądu elektrycznego, determinującymi przewodnictwo materiału są ich koncentracja i ruchliwość. Prąd elektryczny w przewodnikach płynie od potencjału wyższego, do potencjału niższego. By było to możliwe, w obwodzie zamkniętym musi znajdować się element, który zapewni dostarczenie nośników ładunku z punktów o niższym potencjale do punktów o wyższym potencjale, czyli w kierunku przeciwnym do działającego na nie pola elektrycznego. Wymaga to dostarczenia energii i dzieje się w elementach nazywanych źródłami prądu. Rolę chwilowego źródła energii w obwodzie może pełnić również element inercyjny (mający zdolność gromadzenia energii) - uprzednio naładowany kondensator, albo cewka indukcyjna z energią zgromadzoną w jej polu magnetycznym.

Natężenie prądu:

Wielkością opisującą prąd elektryczny jest natężenie prądu elektrycznego I, które definiuje się, jako stosunek ładunku, który przepływa przez poprzeczny przekrój przewodnika do czasu przepływu tego ładunku t:

Definicja ta określa średnią wartość prądu w czasie t. By określić wartość chwilową, należy posłużyć się pochodną ładunku elektrycznego q po czasie t:

Jednostką natężenia prądu elektrycznego w układzie SI jest amper [A].

Natężenie prądu I można wyrazić też przez liczbę ładunków przepływających z prędkością v przez powierzchnię S:

gdzie:

n - koncentracja nośników ładunku,

q - ładunek każdego z nośników,

v - składowe prędkości nośników w kierunku prostopadłym do powierzchni S,

Napięcie elektryczne - różnica potencjałów elektrycznych między dwoma punktami obwodu elektrycznego lub pola elektrycznego. Symbolem napięcia jest U. Napięcie elektryczne jest to stosunek pracy wykonanej podczas przenoszenia ładunku elektrycznego między punktami, dla których określa się napięcie, do wartości tego ładunku. Wyraża to wzór

przy czym zakłada się, że przenoszony ładunek jest na tyle mały, iż nie wpływa znacząco na zewnętrzne pole elektryczne. W przypadku źródła napięcia (prądu) elektrycznego napięcie jest jego najważniejszym parametrem i określa zdolność źródła energii elektrycznej do wykonania pracy. Napięcie mierzone na zaciskach źródła napięcia jest mniejsze od siły elektromotorycznej źródła. Różnica spowodowana spadkiem napięcia na oporze wewnętrznym źródła. Zależność pomiędzy spadkami napięć i siłami elektromotorycznymi w obwodach elektrycznych opisuje drugie prawo Kirchhoffa.

Rezystancja (opór, oporność) jest miarą oporu czynnego, z jakim element (opornik) przeciwstawia się przepływowi prądu elektrycznego. Zwyczajowo rezystancję oznacza się symbolem R. Jednostką rezystancji w układzie SI jest om, której symbolem jest Ω. Odwrotność rezystancji to konduktancja, której jednostką jest simens. Dla większości materiałów rezystancja nie zależy od natężenia prądu, wówczas natężenie prądu jest proporcjonalne do przyłożonego napięcia. Zależność ta znana jest jako prawo Ohma:

Gdzie:

I — natężenie prądu elektrycznego,

U — napięcie elektryczne.

Rezystancja przewodnika o jednakowym przekroju poprzecznym do kierunku przepływu prądu jest proporcjonalna do długości przewodnika, odwrotnie proporcjonalna do przekroju i zależy od materiału, co wyraża wzór:

gdzie

l — długość elementu,

S — pole przekroju poprzecznego elementu,

ρ — rezystywność przewodnika.

Rezystywność, zwana oporem właściwym, jest oporem elementu o jednostkowej długości i jednostkowym polu przekroju poprzecznego. Niektóre substancje przejawiają specyficzne właściwości ze względu na rezystancję - zobacz: rezystancja ujemna, nadprzewodnictwo. W obwodach prądu przemiennego natężenie prądu zależy nie tylko do rezystancji, lecz także od reaktancji elementu. Uogólnieniem i rozwinięciem pojęcia rezystancji w obwodach prądu przemiennego na elementy pojemnościowe (kondensator) i indukcyjne (cewka) jest impedancja. Rezystancja jest wówczas częścią rzeczywistą impedancji zespolonej.

Rezystywność (oporność właściwa, opór właściwy) - cecha substancji charakteryzująca rezystancję danego materiału.

Rezystywność jest zazwyczaj oznaczana, jako ρ (mała grecka litera rho). Jednostką rezystywności w układzie SI jest om⋅metr (Ω·m). Odwrotność rezystywności to konduktywność. Rezystywność określa wzór na zależność rezystancji przewodnika od jego wymiarów:

Z czego wynika:

,

gdzie:

R - rezystancja (opór),

S - pole przekroju poprzecznego elementu,

l - długość elementu.

Rezystywność jest wielkością charakterystyczną dla substancji w danej temperaturze. Wraz ze wzrostem temperatury rezystywność metali wzrasta, a półprzewodników maleje. Rezystywność niektórych substancji w niskich temperaturach znika całkowicie; zjawisko to nazywa się nadprzewodnictwem.

Tabela rezystywności niektórych substancji (w temp. 20 °C)

materiał	rezystywność (Ω·m)
srebro	1,59 · 10^−8
miedź	1,7 · 10^−8
złoto	2,44 · 10^−8
aluminium	2,82 · 10^−8
nikiel	6,99 · 10^−8
żelazo	10 · 10^−8
cyna	1,09 · 10^−7
platyna	11 · 10^−8
ołów	22 · 10^−8
węgiel	3,5 · 10^−5
german	0,46
krzem	640
szkło	10^10 - 10^14
guma	około 10^13
siarka	10^15

Prawo Ohma kojarzone jest zazwyczaj z pierwszym prawem Ohma, czyli proporcjonalności napięcia U mierzonego na końcach przewodnika o oporze R do natężenia prądu płynącego przez ten przewodnik I, co wyraża się wzorem:

Pierwsze prawo Ohma:

Natężenie prądu stałego I jest proporcjonalne do całkowitej siły elektromotorycznej w obwodzie zamkniętym lub do różnicy potencjałów (napięcia elektrycznego U) między końcami części obwodu nie zawierającej źródeł siły elektromotorycznej.

Prawidłowość tę odkrył w 1827 roku niemiecki fizyk, profesor politechniki w Norymberdze i uniwersytetu w Monachium Georg Simon Ohm. Można ją opisać, jako:

Współczynnik proporcjonalności w tej relacji nazywany jest konduktancją, oznaczaną przez G.

Lub w ujęciu tradycyjnym:

Odwrotność konduktancji nazywa się rezystancją (lub oporem elektrycznym) przewodnika i oznaczana jest wielką literą R:

Prawo Ohma określa opór elektryczny przewodnika:

Prawo to jest prawem doświadczalnym i jest dość dokładnie spełnione dla ustalonych warunków przepływu prądu, szczególnie temperatury przewodnika. Materiały, które się do niego stosują, nazywamy przewodnikami omowymi lub "przewodnikami liniowymi" - w odróżnieniu od przewodników nieliniowych, w których opór jest funkcją natężenia płynącego przez nie prądu. Prawo to także nie jest spełnione, gdy zmieniają się parametry przewodnika, szczególnie temperatura. Ze wszystkich materiałów przewodzących prawo Ohma najdokładniej jest spełnione w przypadku metali.

Drugie prawo Ohma

Opór odcinka przewodnika o stałym przekroju poprzecznym jest proporcjonalny do długości tego odcinka i odwrotnie proporcjonalny do pola powierzchni przekroju

Prawo to można wyprowadzić z pierwszego prawa Ohma. Niech odcinek przewodnika o długości l ma ustalone pole powierzchni przekroju poprzecznego, wynoszące S. Jeśli do końców tego odcinka przyłożone zostanie napięcie U, to pole elektryczne wewnątrz przewodnika wyniesie:

Korzystając z definicji gęstości prądu, jako ilorazu natężenia prądu przez pole przekroju przewodnika, w którym płynie prąd, dostajemy:

.

Korzystając z definicji różniczkowego prawa Ohma:

Korzystając z pierwszego prawa Ohma, oraz jeśli oznaczymy opór elektryczny właściwy, jako:

Otrzymujemy drugie prawa Ohma.

Pierwsze prawo Kirchhoffa - prawo dotyczące przepływu prądu w rozgałęzieniach obwodu elektrycznego, sformułowane w 1845 roku przez Gustawa Kirchhoffa. Prawo to wynika z zasady zachowania ładunku, czyli równania ciągłości. Wraz z drugim prawem Kirchhoffa umożliwia określenie wartości i kierunków prądów w obwodach elektrycznych.

Obwody elektryczne:

Węzeł z prądami wpływającymi i wypływającymi (rysunek)

Dla węzła w obwodzie elektrycznym prawo to brzmi:

Dla węzła obwodu elektrycznego suma algebraiczna natężeń prądów wpływających(+) i wypływających(-) jest równa 0 (znak prądu wynika z przyjętej konwencji)

lub

Suma natężeń prądów wpływających do węzła jest równa sumie natężeń prądów wypływających z tego węzła.

Dla przypadku przedstawionego na rysunku I prawo Kirchhoffa można, więc zapisać w postaci:

Przyjmując konwencję, że prądy wpływające do węzła są dodatnie, zaś wypływające są ujemne i traktując je jak wielkości algebraiczne lub w postaci:

Biorąc pod uwagę tylko wartości prądów i zapisując prądy wpływające po jednej, a prądy wypływające po drugiej stronie równania.

W ogólnym przypadku wielu prądów prawo ma postać:

Przy czym należy pamiętać, że prądom wypływającym przypisuje się ujemną wartość natężenia.

Drugie prawo Kirchhoffa - zwane również prawem napięciowym, dotyczy bilansu napięć w zamkniętym obwodzie elektrycznym prądu stałego. Prawo to zostało sformułowane przez niemieckiego fizyka Gustava Kirchhoffa. Najczęściej prawo to jest formułowane w postaci:

W zamkniętym obwodzie suma spadków napięć na oporach równa jest sumie sił elektromotorycznych występujących w tym obwodzie

Przy czym obwód ten może być elementem większej sieci. Wówczas nosi on nazwę oczka sieci. Prawo to zapisane równaniem ma postać

Gdzie:

- SEM k-tego źródła napięcia;

- spadek napięcia na i-tym elemencie oczka.

Dla oporów omowych

gdzie I_i jest natężeniem prądu płynącego przez opornik o oporze R_i.

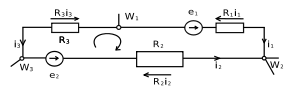
Przykładowe oczko obwodu zamkniętego spełniające drugie prawo Kirchhoffa

Zarówno spadki napięcia jak i siły elektromotoryczne mogą przybierać wartości ujemne i dodatnie. Ich znak ustala się w sposób:

• ustala się kierunek obiegu obwodu (np. zgodnie z ruchem wskazówek zegara

• gdy kierunek prądu jest zgodny z kierunkiem obiegu, spadek napięcia jest dodatni (w przypadku niezgodności - ujemny)

• gdy SEM jest spolaryzowana zgodnie z kierunkiem obiegu, jej wartość jest dodatnia

Prawo to można wywieść z faktu, że krążenie wektora pola elektrycznego po zamkniętym konturze ma wartość 0, jeżeli kontur ten zawarty jest w obwodzie prądu stałego przy braku zmian pola magnetycznego przepływającego przez ten obwód, czyli

Traktując spadek napięcia, jako jego ujemny przyrost, można II prawo Kirchhoffa sformułować następująco

Suma spadków napięcia w obwodzie zamkniętym jest równa zeru

Przykład:

Dla przykładowego obwodu zamkniętego (pokazanego na rysunku) z prawa napięciowego wynikają następujące własności:

gdzie rezystancja wypadkowa jest równa:

Widać stąd, że w przypadku nierozgałęzionego obwodu II prawo Kirchhoffa redukuje się do prawa Ohma.

2.   Opór zastępczy, łączenie oporów.

Opór zastępczy oporników, łączenie oporów:

Każdy element obwodu elektrycznego posiada swój opór. Sposób połączenia tych elementów ma wpływ na opór całego układu. Oporniki połączone szeregowo przedstawione są na rysunku:

Opór zastępczy oporników połączonych szeregowo jest równy sumie oporów poszczególnych oporników:

Oznacza to, że kilka oporników połączonych szeregowo można zastąpić jednym opornikiem, którego wartość jest równa ich sumie.

Oporniki połączone równolegle przedstawione są na rysunku:

Odwrotność oporu zastępczego oporników połączonych równolegle jest równa sumie odwrotności oporów poszczególnych oporników:

3. Kondensator, pojemność kondensatora.

Kondensator - jest to element elektryczny (elektroniczny), zbudowany z dwóch przewodników (okładek) rozdzielonych dielektrykiem.

Doprowadzenie napięcia do okładek kondensatora powoduje zgromadzenie się na nich ładunku elektrycznego. Po odłączeniu od źródła napięcia, ładunki utrzymują się na okładkach siłami przyciągania elektrostatycznego. Jeżeli kondensator, jako całość, nie jest naelektryzowany to cały ładunek zgromadzony na obu okładkach jest jednakowy, co do wartości, ale przeciwnego znaku. Kondensator charakteryzuje pojemność określająca zdolność kondensatora do gromadzenia ładunku:

gdzie:

C - pojemność, w faradach

Q - ładunek zgromadzony na jednej okładce, w kulombach

U - napięcie elektryczne między okładkami, w woltach.

Pojemność wyrażana jest w faradach. Jeden farad to bardzo duża jednostka, dlatego w praktyce spotyka się kondensatory o pojemnościach piko-, nano-, mikro- i milifaradów.

Zależność pojemności od kształtu i rozmiaru:

W poniższych wzorach
jest przenikalnością elektryczną próżni, zaś
- względną przenikalnością elektryczną ośrodka, z którego wykonano dzielący okładki izolator.

Pojemność kondensatora płaskiego:

gdzie:

S - powierzchnia okładek kondensatora,

d - odległość między okładkami.

Pojemność kondensatora walcowego:

gdzie:

l - długość okładek kondensatora walcowego,

r₁ - promień wewnętrznej okładki kondensatora,

r₂ - promień zewnętrznej okładki kondensatora.

Pojemność kondensatora kulistego:

gdzie:

r₁ - promień wewnętrznej okładki kondensatora,

r₂ - promień zewnętrznej okładki kondensatora.

4.   Ładowanie i rozładowanie kondensatora przez opór.

5. Elektryczny model komórki.

Właściwości elektryczne tkanek i całych obiektów biologicznych uwarunkowane są właściwościami komórek oraz ich części strukturalnych i właściwościami substancji międzykomórkowej. Badając przewodnictwo komórki trzeba rozpatrzyć poszczególne jej elementy:

1. cytoplazma - wykazuje cechy złożonego elektrolitu; jej przewodność zależy od koncentracji poszczególnych rodzajów jonów i ich ruchliwości; największe znaczenie mają jony małe, gdyż są one najbardziej ruchliwe (
   ,
   ,
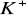
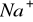
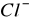
   ); przewodność cytoplazmy krwinek czerwonych wynosi około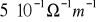
   

2. błona komórkowa - jest izolatorem, decyduje o tym warstwa lipidowa, której przewodność elektryczna mieści się w granicach
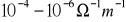
   , a wartość przenikalności elektrycznej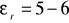
   . Dla większości komórek pojemność błony komórkowej wynosi około
   .

3. pozostałe elementy morfotyczne wykazują cechy półprzewodników; substancje te mają strukturę quasi-krystaliczną i zachodzące w nich procesy można wyjaśnić jedynie na gruncie teorii z fizyki ciała stałego (np. teoria pasmowa kryształów).

Impedancja elektryczna komórki i tkanek

Impedancją elektryczną (Z) nazywamy opór wypadkowy między oporem właściwym (rezystancją) i pojemnościowym (reaktancją). W poniższych obwodach połączono opornik R z kondensatorem C: szeregowo i równolegle.

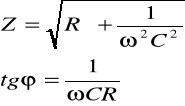
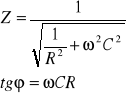
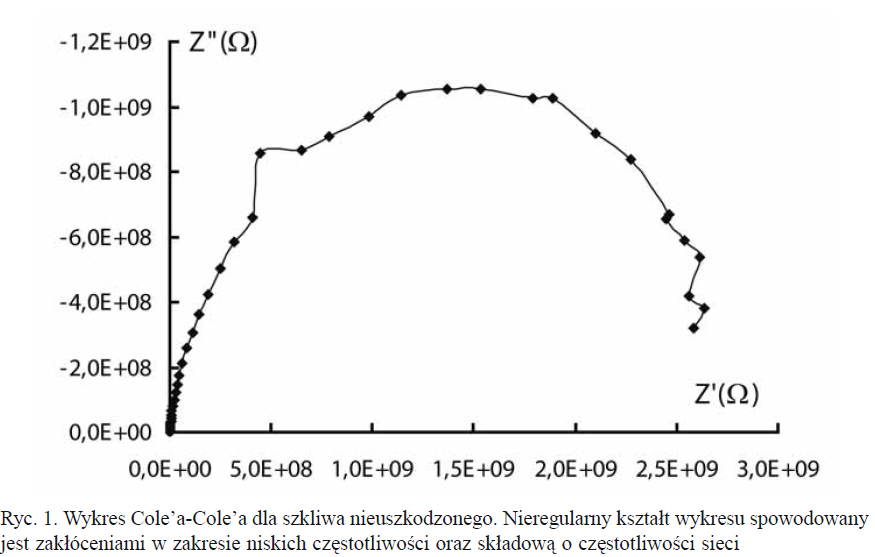
jest kątem przesunięcia fazowego. Obie funkcje składowe impedancji są funkcjami częstotliwości prądu elektrycznego. Zależność częstotliwościową impedancji tkanek można przedstawić w postaci wektorowego wykresu kołowego. Wykres taki otrzymuje się zaznaczając punkty odpowiadające wartościom oporu właściwego i pojemnościowego przy danej częstotliwości. Cechą charakterystyczną komórek żywych, widoczną na tym wykresie, zwanym wykresem Cole'a-Cole'a, jest fakt, iż dla częstotliwości niższych od
i większych od
obiekt biologiczny wykazuje praktycznie tylko opór rzeczywisty.

W analizie przewodzenia prądu zmiennego przez obiekty żywe symulujemy ich zachowanie się kombinacjami rozpatrzonych obwodów. Modele takie nazywamy elektrycznymi obwodami zastępczymi. Na schemacie obok
i
to odpowiednio rezystancja i pojemność elektryczna błony,
- opór cytoplazmy,
- opór rzeczywisty płynu międzykomórkowego. Obiekty biologiczne nie wykazują indukcyjności. Dyspersja impedancji może być wykorzystywana w diagnostyce medycznej do jakościowej oceny stanów fizjologicznych. Okazuje się również, że przy działaniu na tkanki niektórymi czynnikami fizykochemicznymi przebiegi krzywych dyspersyjnych ulegają wyraźnym zmianom.

Dyspersja przenikalności i przewodności elektrycznej tkanek

Przenikalność i przewodność elektryczna komórek żywych wykazują zależność od częstotliwości pola elektrycznego. Przy niewielkich częstotliwościach, wskutek dużego oporu elektrycznego błony, następuje izolacja jonów we wnętrzu komórki i zostaje indukowany dipol, a wartość przenikalności elektrycznej jest bardzo duża. Ze wzrostem częstotliwości efekt ten zanika, aż do sytuacji, gdy opór pojemnościowy błony zawiera wyłącznie opór błony lipidowej, a wnętrze komórki bierze udział w przewodzeniu prądu. Zależność częstotliwościowa, zwana dyspersją, przewodności i przenikalności elektrycznej występuje dla wszystkich rodzajów tkanek. Wykres przedstawia główne zakresy dyspersji przenikalności elektrycznej dla tkanek o dużej i średniej zawartości wody w komórkach (np. dla krwi). Przebieg zależności częstotliwościowej przewodności jest w przybliżeniu symetryczny w zakresie tzw. 
-dyspersji.

Początkowy obszar dyspersji stanowi superpozycję kilku zakresów, które doświadczalnie trudno oddzielić od polaryzacji elektrodowej. Brak jest dotychczas teorii, która wyjaśniałaby źródła dyspersji w tym zakresie częstotliwości.

Obszar
-dyspersji obejmuje niskie częstotliwości (od kilku Hz do kilku tysięcy Hz). Częstotliwość relaksacyjna średnia tej dyspersji
zależy m.in. od wymiarów komórek i od struktury ich warstw powierzchniowych.

-dyspersja obejmuje częstotliwości od kilkudziesięciu kHz do około 30MHz, o częstotliwości średniej
. Jej źródłem jest niejednorodna struktura fizyczna tkanek biologicznych (obecność błon komórkowych). W obszarze powyżej kilkudziesięciu MHz występuje obszar płaski, w którym przenikalność elektryczna krwi jest mniejsza niż wody.

Dyspersja
stanowi również superpozycję kilku zakresów i występuje w zakresie od kilkuset MHz do kilku gigaherców. Jest ona związana z właściwościami polarnymi biomolekuł wody związanej. W zakresie mikrofalowym występuje dyspersja wody wolnej (obszar dyspersji
).

Hematokryt a rezystywność komórki

Z powyższych rozważań wynika, że przy niskich częstotliwościach opór właściwy krwi zależy od liczby erytrocytów, a właściwie od hematokrytu. Wzór Maxwella przyjmuje postać:

,

gdzie
- stosunek objętości fazy stałej do objętości całego suspensoidu (odpowiada hematokrytowi),
- opór właściwy krwi,
- opór właściwy osocza.

6. Niepewności pomiarowe - błąd bezwzględny, względny i względny procentowy.

Błąd pomiaru - odstępstwo wyniku jednostkowego pomiaru od wartości prawdziwej, której wielkości na ogół nie znamy. Nie należy go rozumieć, jako powstałego wyłącznie w wyniku pomyłki, a jako nieodłączny czynnik procesu pomiarowego. Błąd pomiaru jest bezpośrednio związany z metodą pomiaru. Wykonując pomiary nawet tym samym przyrządem otrzymamy często różne wyniki. Błędy przy pomiarach dzielimy na:

Błąd względny w metrologii i statystyce to iloraz błędu bezwzględnego i wartości dokładnej x₀

gdzie

x - wartość mierzona,

Δx - błąd bezwzględny.

przy czym zazwyczaj, gdy błąd jest błędem losowym, określa się moduł błędu względnego

Błąd względny jest bezwymiarowy, najczęściej wyrażany w procentach

i nazywany jest wówczas błędem procentowym. Jeśli błąd jest bardzo mały, używa się również promili. W metrologii służy głównie do oceny dokładności przyrządów pomiarowych pracujących na różnych zakresach pomiarowych. W statystyce porównywane są w ten sposób wariancje rozkładów różniących się wartością oczekiwaną np. błędy prognoz dwóch różnych wielkości.

Błędem bezwzględnym nazywa się różnicę pomiędzy wartością zmierzoną x, a wartością dokładną x₀

przy czym wartość dokładna nie jest znana. Może być ona określona w sposób przybliżony np. jako wynik teoretycznych obliczeń, średnia arytmetyczna wzięta z dużej liczby pomiarów lub jako założony parametr w procesie technologicznym. Może to być również wynik pomiaru przyrządem charakteryzującym się znacznie większą dokładnością.

Pomiar zawsze obarczony jest błędem pomiarowym, ponieważ dokonywany jest za pomocą przyrządu pomiarowego, np. woltomierza, amperomierza, suwmiarki, o skończonej dokładności.

Wartość błędu może zostać również obliczona według podanej klasy miernika analogowego. Błąd bezwzględny pomiaru oblicza się wówczas z wykorzystaniem wzoru:

gdzie

kl - klasa,

Z - zakres.

Oznacza to, że w każdym punkcie podziałki danego miernika może nastąpić błąd mieszczący się w granicach wartości mierzonej

Jeżeli przyrząd pomiarowy wyposażony jest w podziałkę i nie jest podana klasa przyrządu (np. linijka, kątomierz, mechaniczna waga szalkowa, mechaniczny stoper), wówczas niepewność pojedynczego pomiaru nie może być mniejsza od wartości wyznaczonej przez najmniejszą odległość między działkami podziałki.

W błędach systematycznych:

W przypadku błędu systematycznego, jeżeli jego wartość jest przewidywalna i znana (np. związana ze znaną zmianą temperatury), wartość błędu bezwzględnego nazywana jest poprawką. Po dodaniu poprawki do wyniku pomiaru x otrzymuje się wartość skorygowaną o błąd systematyczny. Poprawka może mieć wartość ujemną lub dodatnią, w zależności od czynnika wpływającego na zmianę wartości pomiaru.

W błędach losowych:

W przypadku błędów losowych, inaczej niż w błędach systematycznych, nie jest istotne, czy odchylenie wyniku pomiaru od wartości oczekiwanej nastąpiło w górę, czy w dół, dlatego rozpatruje się moduł błędu bezwzględnego

Zerknij na tę stronę może Cię zaskoczy:

http://biofizyka.cm.umk.pl/pracownia1/download/zag_15.htm

Tu masz jeszcze trochę więcej o błonie komórkowej:

http://www.ib.uph.edu.pl/bk_blony.htm

---