Proces odwracalny, kiedy proces rzeczywisty może być taki, cykl przemian, opisać cykle Carnota.
Procesem odwracalnym nazywamy taki proces ,w którym przemiany stanu układu mogą się odbywać w obu kierunkach. Układ termodynamiczny ulega przemianie odwracalnej wtedy gdy przechodzi przez te same stany zarówno w jednym jak i w drugim kierunku zaś po powrocie do stanu wyjściowego nie można zaobserwować żadnych zmian układu ani otoczenia. Każdy rzeczywisty proces jest nieodwracalny - podczas takiego procesu zachodzą nieodwracalne zmiany układu i otoczenia.
Cykl przemian jest to proces którego układ przechodząc przez szereg różnych stanów powraca do stanu początkowego po innej drodze niż w procesach odwracalnych. W procesie cyklicznym energia jest stała.
Przykładem cyklu przemian jest cykl Carnota, składa się on z dwóch izoterm(dla temp. T1,T2) oraz z dwóch adiabat. Cykl rozpoczyna się od przystawienia dna cylindra do grzejnicy o temp.T1.Dno cylindra przystawiamy do ściany nie przepuszczającej ciepła. Od tego momentu gaz rozpręża się dalej adiabatycznie do objętości. Procesy adiabatyczne pełnią w tym cyklu tylko rolę pomocniczą - pozwalają przejść z jednej izotermy na drugą.
Sprawność cyklu Carnota:![]()
współczynnik sprawności cyklu Carnota zależy tylko od temp. źródła ciepła T1 i chłodnicy T2. Cykl Carnota wyznacza granicę sprawności wszystkich silników cieplnych.
Obieg cyklu Carnota składa się z czterech czynników:
rozprężenia izotermiczne ze źródła ciepła
rozprężenie adiabatyczne
sprężanie izotermiczne z chłodnicy
sprężanie adiabatyczne
Tw. Carnota:
1.Odwracalny cykl Carnota przeprowadzony z dowolnym ciałem roboczym ma tę samą sprawność co cykl Carnota przeprowadzony z gazem doskonałym.
2.Sprawność nieodwracalnego CC nie może być większa niż sprawność odwracalnego CC.
2 zasada dynamiki, siła Lorentza, siła elektrodynamiczna (lub elektrostatyczna)- diamagnetyzm.
2 zasada termodynamiki - niemożliwe jest zbudowanie silnika cieplnego który zamieniał by stale ciepło na pracę korzystając tylko z jednego źródła ciepła. Silnik działa tylko wtedy gdy istnieją dwa źródła ciepła - grzejnica i chłodnica - o różnych temp.
Istnieją również inne równoważne sformułowania drugiej zasady dynamiki:
nie można zbudować perpetum mobile drugiego rodzaju,
ciepło nie może przepływać samorzutnie od ciała o niższej temp. Do ciała o wyższej temp.
W układzie zamkniętym mogą zachodzić tylko takie procesy termodynamiczne podczas których entropia nie zmienna się lub rośnie.
Siłą Lorentza nazywamy siłę która działa na cząstkę naładowaną poruszającą się w polu elektromagnetycznym (elektrycznym i magnetycznym) jest ona określona wzorem:![]()
F - siła Lorentza
q -ładunek elektryczny cząstki
v -prędkość cząstki
E - natężenie pola elektrycznego
B - indukcja pola magnetycznego
W przypadku gdy cząstka porusza się w polu magnetycznym siła Lorentza przyjmuje wartość
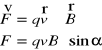
α - kąt pomiędzy kierunkiem indukcji pola magnetycznego a kierunkiem prędkości ładunku.
Zwrot siły działającej na poruszającą się cząstkę naładowaną dodatnio określa reguła śruby prawoskrętnej.
Siłą elektrodynamiczną nazywamy siłę działającą na przewodnik z prądem umieszczony w polu magnetycznym. Jej wartość jest wprost proporcjonalna do długości czynnej przewodnika (część przewodnika znajdująca się w polu magnetycznym) natężenie płynącego przez przewód prądu zależy od wartości indukcji
pola magnetycznego. Siła elektrodynamiczna określona jest wzorem
![]()
F - siła elektrodynamiczna
I - natężenie prądu
![]()
- wektor o długości równej długości przewodnika i o zwrocie zgodnym z kierunkiem przepływu prądu
B - wektor indukcji magnetycznej
Wartość siły elektromagnetycznej jest równa
F = I l B sinα
α - kąt pomiędzy wektorem I i B
Wektor siły elektrodynamicznej jest prostopadły do płaszczyzny w której leżą wektory I i B zaś jego zwrot określa reguła śruby prawoskrętnej lub reguła lewej dłoni.
Diamagnetyzm - zjawisko wzbudzenia dodatkowego momentu magnetycznego w powłokach elektronowych atomów pod wpływem działania zewnętrznego pola magnetycznego . Ponieważ z dowolnym kołowym ruchem ładunków elektrycznych wiąże się powstanie momentu magnetycznego , a w przypadku atomu mamy do czynienia z ruchem orbitalnym elektronów i ich obrotem wokół własnych osi (spin ) , związane z nimi są dwa momenty magnetyczny orbitalny i spinowy .
Istnieją przypadki gdy , oba te momenty są równe co do wartości, lecz przeciwnie skierowane i wzajemnie się znoszą . Atom o takich właściwościach nie będzie się zachowywał jak elementarny magnes . Równowagę tę można jednak zakłócić przykładając zewnętrzne pole magnetyczne , które indukuje w powłokach elektronowych dodatkowy prąd i związany z nim dodatkowy moment magnetyczny . W myśl reguły Lentza dodatkowe pole magnetyczne powinno osłabić pole magnetyczne , które je wywołało , a zatem zewnętrzne pole magnetyczne .
diamagnetyk umieszczony w polu magnetycznym tylko nieznacznie wpływa na to pole w którym się znajduje. Dla diamagnetyków wartość indukcji pola magnetycznego wytworzonego w ich wnętrzu jest nieco mniejsza od wartości indukcji otaczającego zewnętrznego pola magnetycznego a więc względna przenikalność magnetyczna jest dla diamagnetyków nieznacznie mniejsza od jedności. Diamagnetykami są np. ołów cynk i miedź.
Prawo Ampera, prawo Biota Sawarta. Natężenie pola magnetycznego w otoczeniu prostego i długiego przewodnika, w środku przewodnika kołowego, we wnętrzu solenoidu.
Prawo Ampera - krążenie wektora natężenia pola magnetycznego po dowolnej krzywej zamkniętej jest równe
Algebraicznej sumie natężeń prądów przepływających przez powierzchnię napiętą na tej krzywej.
![]()
Hi - wektor natężenia pola magnetycznego na i - tym odcinku krzywej
Δli - wektor przypisany i - temu odcinkowi krzywej (wektor natężenia pola magnetycznego w każdym punkcie danego odcinka Δl jest jednakowy zwrot każdemu odcinkowi przypisuje się zgodny z umownym kierunkiem obiegu po krzywej)
Ik - natężenie k - tego prądu
n - liczba odcinków na które została podzielona krzywa
m. - liczba prądów przepływających przez powierzchnię napiętą na krzywej.
Prawo Biota Sawarta - prawo to pozwala wyznaczyć pole magnetyczne wytwarzane przez dodatkowy cienki przewód o dowolnym kształcie w którym płynie prąd.
![]()
I - natężenie prądu w przewodzie
dH - wektor indukcji pola magnetycznego wytworzonego w punkcie przez prąd elementarny
dl - wektor długości elementu skierowany zgodnie z kierunkiem przepływu prądu
r - wektor położenia punktu względem długości elementu
α - kąt pomiędzy wektorami dl i r
np. - pole w środku pętli, pole na osi pętli.
Połączenie szeregowe. Prawo Ohma dla prądu zmiennego, natężenie, zawada, napięcie, opór.
Połączenia szeregowe:
kondensatorów- pojemność zastępcza układu w kondensatorze 1/C=(suma)1/Ci . różnice potencjałów okładkami kolejnych kondensatorów dodają się. Z kolei zgromadzone na każdej z okładek dowolnego kondensatora ładunki są co do bezwzględnej wartości takie same U=(suma)Ui ale U=Q/C oraz Ui=Q/Ci
rezystorów - prąd przepływa kolejno przez każdy opornik układu szeregowego połączonych oporników nie ma węzłów. Spadek nap na oporniku zastępczym jest = sumie spadków nap na poszczególnych opornikach. Przykładowo : IRz=IR1+IR2+...+IRn wtedy Rz=R1+R2+...+Rn
Prawo Ohma dla prądu zmiennego :Uc - nap na kondensatorze , U=Uocos(omega)t -nap przyłożone do obwodu . prąd płynący w obwodzie RLC w funkcji czasu I=Icos(omega t- strumień) , (omega t)- częstość drgań , (strumień)- przesunięcie fazowe miedzy prądem a nap
Tg (fi)=[(omega)L-1/(ome)C]/R , Io=Uo/Z , z- zawada Z=R^2+(Xc-XL)^2
Prawo Ohma określa związek między nap Uo przyłożonego do obwodu a amplitudą prądu Io płynącego w obwodzie. Prawo Ohma dla prądu zmiennego jest podobne w formie dla U=RI z tym że zamiast oporu omowego we wzorze występuje zawada Z=R^2+(XL-XC)^2
Zawada - impedancja gałęzi szeregowej RLC
Siła bezwładności. Jak nazywają się siły bezwładności które obserwujemy w układzie Ziemia.
Jeżeli układ odniesienia porusza się ruchem postępowym przyśpieszonym lub obraca się względem pewnego inercjału układu odniesienia to taki układ nazywamy nieinercjalnym .
W układzie nieinercjalnym pojawią się dodatkowo siły pozorne zwane siłami bezwładności.
Nazwa sił pozornych pochodzi stąd że obserwator nieruchomy ich nie dostrzega. Widzi je tylko obserwator znajdujący się ruchu , ale i on nie jest w stanie znaleźć ciał od których siły te mogły by pochodzić Fb=-ma F,[a wektory(ze strzałką)]
przyśpieszenie układu
Fb- siła działająca na ciało o masie m w wewnętrznym układzie odniesienia poruszający się ruchem postępowym z prędkością a.
Na rys przedstawiono ciało o masie m znajdujące się na wózku poruszającym się ruchem postępowym z przyśpieszeniem a. Oczywiście wózek stanowi nieinercjalny układ odniesienia. Jeżeli żadna inna siła nie działa w kierunku ruchu na ciało znajduje się na wózku (nie ma siły tarcia) to w układzie odniesienia związanym z wózkiem ciało będzie się poruszać z przyśpieszeniem równym (-a) . obserwator na ziemi (inercjalny układ odniesienia ) stwierdzi że ciało nie porusza się względem niego (zaobserwuje on uciekający od nieruchomego ciała wózek ). Jeżeli założymy że działa siła tarcia między wózkiem a ciałem to obserwator na wózku zaobserwuje spoczywające ciało (siła tarcia równoważy siłę bezwładności )z kolei obserwator na ziemi stwierdzi że ciało porusza się wraz z wózkiem z przyśpieszeniem = a (a-wektor)
Siła odśrodkowa bezwładności F = m.....^2r
Siła b. Coridisa- pojawia się jeśli ciało porusza się wzgl. wirującego ukł. odniesienia. Jest ona skierowana prostopadle do V ciała i ω kątowej obracającego się układu . znika gdy ciało w układzie wirującym spoczywa tzn. V=0 oraz gdy ciało porusza się równolegle do osi obrotu układu tzn. V (równoległe do ) ω
Na swobodnie spadające ciało działa siła Coridisa powodując odchylenie toru ciała od pionu w kierunku wschodnim. Siła ta jest maksymalna na równiku a=0 na biegunach. Ciało wyrzucone na północ będzie odchylone na wschodniej na półkuli północnej oraz na zachodniej na płk południowej.
Opisać na przykładzie zjawisko indukcji elektromagnetycznej, prawo Faradaja, regułę Lenza.
Zjawiskiem indukcji elektromagnetycznej nazywamy zjawisko powstawania prądu w zamkniętym obwodzie pod wpływem zmian strumienia indukcji magnetycznej. Powstający prąd nazywamy prądem indukcyjnym. Może on zostać wzbudzony w zamkniętym obwodzie wtedy gdy zmienia się strumień indukcji pola magnetycznego obejmowany przez obwód.
Reguła Lenza pozwala określić kierunek prądu indukcyjnego. Prąd indukcyjny ma zawsze taki kierunek Ze wytworzone przez niego pole magnetyczne przeciwdziała przyczynie która go wywołuje(co wynika z zasady zachowania energii. Przykład:
Podczas zbliżania magnesu do cewki wzbudza się prąd indukcyjny. Przyczyną wzbudzenia prądu jest więc zbliżenie do cewki północnego bieguna magnesu. Przeciwdziałaniem jest odpychanie bieguna jednoimiennego. Powoduje to wytworzenie wokół cewki pola magnetycznego skierowanego biegunem N w stronę magnesu.
Prawo Faradaja - wartość siły elektromotorycznej indukcji jest równa zmianie strumienia magnetycznego Δφ podzielonej przez przyrost czasu Δt w którym ta zmiana nastąpiła (siła elektromotoryczna indukcji jest proporcjonalna do szybkości zmian strumienia magnetycznego)
![]()
![]()
Sił elektromotoryczna indukcji powstająca wskutek zjawiska indukcji elektromagnetycznej jest przyczyną przepływu prądu indukcyjnego w zamkniętym obwodzie. Jej miarą jest stosunek pracy ΔW wykonanej przez siły zewnętrzne powodujące przepływ przez przewodnik ładunku Δq do wartości tego ładunku.
![]()
Po jakich krzywych porusza się ładunek elektryczny, np. proton w polu magnetycznym i elektrycznym, gdy wpadnie w to pole prostopadle do linii sił.
Siła działająca na ładunek q umieszczony w polu o natężeniu E wynosi F=q*E. Jeżeli ładunek ulega przesunięciu wtedy siły pola elektrycznego wykonuje pracę W . Praca ta może być dodatnia lub ujemna gdy siły zewnętrzne wykonują pracę przeciwko siłom pola elektrycznego.
Załóżmy że w polu elektrycznym przez dodat. ładunek nastąpiło przesunięcie ładunku qo wzdłuż krzywej „l”. Praca wykonana podczas jego przesunięcia wynosi: dW=FdL=qEdL=qoEdLcos...
Praca wykonana na całym ..........E=q*dLcos.../4*3,14Er^2
Ze wzoru wynika że praca wytworzona przy przesunięciu ładunku elektrycznego , w polu elektrycznym zależy wyłącznie od położenia początkowego i końcowego ładunku, nie zależy zaś od kształtu drogi.
1 zasada termodynamiki.
1 zasada termodynamiki - zmiana energii wewnętrznej ciała jest równa sumie algebraicznej pracy wykonanej nad ciałem przez siły zewnętrzne i ciepła wymienionego z otoczeniem.
ΔEw=W+Q
ΔEw - zmiana energii wewnętrznej
W - wykonana praca
Q - ciepło wymienione z otoczeniem.
Kiedy zachodzi precesja a kiedy nutacja na przykładzie bąka.
Żyroskopem albo bąkiem nazywamy ciało wirujące wokół osi, które może przyjąć dowolny kierunek w przestrzeni unieruchomionej co najwyżej w jednym tylko punkcie . najczęściej mamy do czynienia z bąkiem symetrycznym tzn. z bryłami mającymi symetrię dośrodkowe. Bąki symetryczne dzielimy na spłaszczone , gdy oś symetrii jest osią max. momentu bezwładności oraz wydłużone , gdy oś jest osią minimalnego momentu bezwładności.
Nutacja-ruch bąka na który nie działają żadne momenty sił lub gdy suma działających na niego momentów =0. Z tego wynika że w czasie nutacji bąk podlega prawu zachowania krętu. Zachowując więc swój kierunek w przestrzeni , prosta na której leży wektor krętu nazywamy osią krętu.
Przykładem nutacji jest ruch wirowy nieprawidłowo rzuconego dysku. Prawidłowo rzucony dysk powinien wirować beznutacyjnie. Jego płaszczyzna tworzy wtedy na drugiej opadającej części toru , z kierunkiem toru pewien kąt dzięki czemu powstaje , podobnie jak na skrzydłach samolotu siła nośna. Dzięki tej sile dysk nie leci po paraboli, lecz po krzywej przez co uzyskuje większy zasięg.
Ruch precesyjny bąka o ciężarze mg, momencie pędu L i środku masy wyznaczonego przez wektor r (rys. a) Precesja-ruch bąka na który działa prostopadły do jego osi moment siły. Obraz ruchu jest podobny do nutacji. Bąk wiruje wokół osi symetrii, a ta równocześnie porusza się po bocznicy pewnego stożka nazywanego stożkiem precesji (oś symetrii precesji jest prostopadła do wektora momentu siły).
Przykłady:
bąk dziecięcy- precesja bąka dziecięcego następuje pod wpływem momentu jaki wywiera na niego para sił ciężkości G oraz reakcji w punkcie podporowym Ro . moment tej pary M , a zatem i kąt przyrost krętu dL jest w każdej chwili poziomy oraz prostopadły do aktualnego krętu L z tego wynika że oś stożka jest pionowa.
precesja pocisków - pociskom armatnim nadaje się przez nagwintowanie lufy ruch obrotowy wokół ich osi podłużnej. Na oś krętu takiego pocisku działa moment siły oporu powietrza, który powoduje przyrost krętu prostopadły do osi podłużnej i kierunku lotu. Warunki są tak dobrane (nagwintowanie lufy )żeby pocisk w czasie lotu wykonywało koło połowy obrotu precesyjnego i w cel uderzył swoja częścią przednią, w której znajduje się zapalnik, a nie np. boczną ścianką. Równocześnie nastąpi spowodowana przez jednostronnie działający opór powietrza niewielkie zboczenie pocisku z płaszczyzny, w której został wystrzelony.
Jak porusza się środek masy pocisku po jego rozerwaniu się podczas lotu i dlaczego.
(m1+m2)=m1x1+m2x2
Ze wzoru wynika że środek masy jest to taki punkt dla którego iloczyn całej masy układu przez jego odległość od początku układu równa się sumie iloczynów mas poszczególnych punktów przez ich odległość od początku układu.
Środek masy układu porusza się tak jakby cała masa układu była w nim skupiona i na niego działały wszystkie siły zewnętrzne. Zatem środek masy układu na który działają siły zewnętrzne porusza się niezależnie od ruchów poszczególnych punktów układu ruchem jednostajnym (v=const )
pocisk wystrzelony z działa : w najwyższym punkcie toru pocisk rozrywa się . Odłamki rozpraszają się , jednak ich środek mas porusza się nadal po tej samej krzywej balistycznej. Siłami zewn. są ciężary odłamków (wynik który zmienia nieco tor jest opór powietrza inny dla całego pocisku , niż dla odłamków).
Prawo Kepplera .
1.Planety poruszają się po elipsach mających jedno ognisko wspólne w którym znajduje się słońce(inna wersja: we wspólnym ognisku znajduje się słońce masy całego układu planetarnego)
2.Promiwń wodzący (ze słońca ) planetę zakreśla w jednakowych odstępach czasu jednakowe pola (w związku z tym prawem można zdefiniować prędkość polową wektora wodzącego jako stosunek powierzchni zakreślonej przez promień wodzący do czasu w którym ją zakreśla i sformułować to prawo następująco: prędkość prędkość polowa planety jest wielkością stałą Vs=const)
3. Kwadraty okresów obiegu planet mają się do siebie tak jak trzecie potęgi ich dużych półosi (T12/T22=a13/a23)
na tej podstawie można je sformułować jako: stosunek kwadratu okresu obiegu do sześcianu dużej półosi ma dla każdej planety jednakową wartość czyli T2/a3=const)
co to jest gaz doskonały, prędkość średnia kwadratowa, prędkość najbardziej prawdopodobna cząstek gazu.
.Gazem doskonałym nazywamy gaz który w dowolnych warunkach zachowywał by się w ten sam prosty sposób. Objętość zajmowana przez gaz doskonały przy stałym ciśnieniu i temp. jest proporcjonalna do jego masy. W rzeczywistości nie ma nic takiego, jak gaz naprawdę doskonały jest to tylko proste i pożyteczne pojęcie związane z rzeczywistością tym, że wszystkie gazy rzeczywiste zbliżają się swoim zachowaniem do abstrakcyjnego gazu doskonałego, jeśli ich gęstość jest dostatecznie mała. Równanie stanu gazu doskonałego pV=nm. RT.
Temperatura gazu doskonałego wynosi 273,160 K.
Gaz doskonały- def. mikroskopowa. Gaz doskonały definiujemy z mikroskopowego punktu widzenia czyniąc następujące założenia: -gaz składa się z cząsteczek, które można traktować jako punkty materialne: -cząsteczki poruszają się chaotycznie i podlegają zasada dynamiki Newtona: -całkowita liczba cząsteczek jest bardzo duża: -objętość cząsteczek jest tak małą częścią objętości zajmowanej przez gaz, że można ją pominąć: -poza momentem zderzenia na cząsteczki nie działają żadne siły: -zderzenia są sprężyste, a czas ich trwania jest do pominięcia.
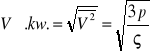
Pierwiastek kwadratowy ze średniego kwadratu prędkości nazywamy średnią prędkością kwadratową i jak wynika z zależności:
![]()
Wartość Vśr.kw. gazu możemy obliczyć ze zmierzonych wartości ciśnienia p i gęstości ς. Tak np. w normalnych warunkach (00C, 760 Tr) cząsteczki tlenu 02 mają Vśr.kw.=461 m/s, zaś wodoru H2-1832 m/s.
![]()
Jak teraz widać wyraźnie, każda z tych prędkości przy ustalonej temp. T, będzie dla różnych gazów różna, zależy ona bowiem jeszcze od masy cząsteczkowej gazu. Im masa cząsteczek jest mniejsza, tym większy jest udział cząsteczek o dużych wartościach prędkości. Dlatego też na dużych wysokościach jest bardziej prawdopodobna ucieczka z atmosfery Ziemi wodoru, niż tlenu czy azotu.
![]()
Prędkość najbardziej prawdopodobna:
Podstawowym założeniem teorii cząsteczkowo -kinetycznej jest to, że ruch cząsteczek jest całkowicie bezładny. Dotyczy to zarówno ruchu postępowego cząsteczek, jak i innych postaci
Tego ruchu-obrotów i drgań. Żaden rodzaj ruchu nie jest uprzywilejowany. Można więc założyć, że średnio na każdy stopień swobody cząsteczki przypada jednakowa ilość energii E. To założenie nazywamy zasadą ekwipartycji (równego rozkładu) energii pomiędzy stopnie swobody. Okazuje się, że wartości tej energii przypadającej na każdy stopień wynosi ½ kT.
Przez liczbę stopni swobody ciała rozumiemy liczbę niezależnych współrzędnych, które należy wprowadzić, aby określić położenie ciała w przestrzeni. Energia ta jak widać, nie zależy ani od objętości, ani od ciśnienia; zależy natomiast od ilości stopni swobody cząsteczek i temperatury. Temperatura jest wielkością statystyczną i możemy o nie mówić, gdy mamy do czynienia z dużą ilością cząsteczek. Gdy ilość cząsteczek jest mała, temp. gazu jest właściwie nieokreślona.
Uszeregować prędkości cząstek gazu: średnia arytmetyczna Va, średnia kwadratowa Vk, najbardziej prawdopodobna Vp.
Średnia arytmetyczna prędkość Va wszystkich cząstek jest nieco większa od prędkości najbardziej prawdopodobnej Vp. Wartość prędkości kwadratowej jest jeszcze większa. Jak widać każda z tych prędkości przy ustalonej temp. Będzie dla różnych gazów różna zależy ona bowiem jeszcze od masy cząsteczkowej gazu. Im masa cząsteczek jest mniejsza tym w określonej temp. Większy jest udział cząstek o dużych wartościach prędkości.
Maxwellowski rozkład prędkości 1000 cząstek tlenu O2 w temp. 0oC.
nr - liczba cząstek o prędkościach zawartych w przedziałach o szerokości co 1 m/s .
Co to jest średni kwadrat prędkości V jaki jestjego związek z prędkością średnią kwadratową Vk
Średnia prędkość kwadratowa - pierwiastek kwadratowy ze średniego kwadratu prędkości
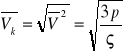
Wartość Vk gazu możemy obliczyć ze zmienionych wartości ciśnienia p i gęstości ς.
Objaśnić zjawisko rezonansu: czego dotyczy? Na czym polega? kiedy występuje? Wykres, w jakim przypadku amplituda mogła by być nieskończonością? Przykład zjawiska.
Jeżeli na układ działa okresowa siła powodująca drgania wymuszone i jeżeli częstotliwość siły wymuszającej jest równa częstotliwości drgań układu(większość ciał ma charakterystyczną częstotliwość drgań własnych). Wtedy występuje zjawisko rezonansu. Polega ono na gwałtownym wzroście amplitudy drgań (do nieskończoności jeżeli nie zostanie uwzględnione tłumienie).Maksimum krzywej rezonansowej przesuwa się w miarę tłumienia w lewo. Jeśli siła tłumienia dąży do zera amplituda dąży do nieskończoności .
Np. fundamenty pod maszynami lub halami fabrycznymi mogą pod wpływem drgań rezonansowych wymuszonych przez maszyny. Zjawisko rezonansu znajduje liczne zastosowanie szczególnie w technice i nauce. Rezonans występuje dla wszystkich rodzajów drgań np. akustycznych, elektromagnetycznych.
Paramagnetyzm:
Paramagnetyki - umieszczenie paramgnetyka w zewnętrznym polu magnetycznym tylko w minimalnym stopniu wpływa na to pole w którym się on znajduje. Dla paramagnetyków wartość indukcji pola magnetycznego wytworzonego w ich wnętrzu jest nieco większa od wartości indukcji otaczającego je zewnętrznego pola magnetycznego a więc względna przenikalność magnetyczna jest dla paramagnetyków nieznacznie większa od jedności.
Prawo braci Curie: km = const/T
Paramagnetyki podlegają prawu Curie gdy spełniony jest warunek pmμ0H<<kT (słabe pole i wysoka temp.)
KT=E - energia przybliżona do średniej energii kinetycznej ruchów cieplnych.
Prawo Curie jest spełnione gdy max. energia potencjalna dipoli w polu magnetycznym jest dużo mniejsza od ich energii. Dla T>>300K prawo Curie jest spełnione, nie obowiązuje ono w temp. Bliskich zeru absolutnemu. Efekt diamagnetyczny w paramagnetykach jest 100 razy większy niż w diamagnetykach. Atomy paramagnetyczne mają własny moment magnetyczny (tylko skręcany).
Prawo Curie - Weissa
Km = const/T±D , gdzie D
Co to jest przemiana adiabatyczna.
Przemiana adiabatyczna jest to taka przemiana podczas której nie występuje wymiana ciepła z otoczeniem a więc kiedy przemiana zachodzi bardzo szybko lub kiedy gaz jest odizolowany cieplnie od otoczenia.
Równanie Poissona opisuje zależność między objętością gazu w przemianie adiabatycznej a jego ciśnieniem
PVk =const
K = Cp/Cv - stosunek ciepła molowego gazu pod stałym ciśnieniem do ciepła molowego gazu przy stałej objętości.
Krzywa przedstawiająca zależność ciśnienia gazu od objętości w przemianie adiabatycznej nazywa się adiabatą. Adiabata jest bardziej stroma niż izoterma ponieważ ciśnienie wzrasta w przemianie adiabatycznej niż w przemianie izotermicznej przemianie adiabatycznej zmiana energii wewnętrznej odbywa się wyłącznie poprzez pracę(Q= const). Praca wykonana w przemianie adiabatycznej równa jest polu zawartemu pod adiabatą. Podczas ogrzewania gazu mogą ulec zmianie wszystkie jego parametry . W tym przypadku 1 mol gazu ogrzewając się o 1K pobiera określoną ilość energii.
Dla gazu doskonałego zachodzi zależność Cp-Cu=R
Linia ciągła - adiabata
Linia przerywana - izoterma
6
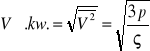
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
rozne4, Politechnika WGGiG, Fizyka
więcej podobnych podstron