ANALIZA STANU NAPRĘŻENIA. Analiza stanu naprężenia polega na przeprowadzeniu obliczeń mających na celu wyznaczenie poszczególnych składowych stanu naprężenia. Stan naprężenia ciała w rozpatrywanym punkcie nazywa się zbiór naprężeń dla wszystkich możliwych położeń elementarnej powierzchni dA. Składowe naprężeń stycznych prostopadłe do krawędzi przecięcia się dwóch wzajemnie prostopadłych przekrojów elementarnych są zawsze równe. Jednoosiowy stan naprężenia - stan naprężenia, w którym tylko jedno z naprężeń głównych jest niezerowe; taka sytuacja ma miejsce w wielu typowych przypadkach ( rozciąganie, zginanie itp.) Płaski stan naprężenia - stan, w którym współrzędne w jednym wierszu i jednej kolumnie (symetrycznego) tensora naprężenia są równe zero; najczęściej nie odpowiada mu jednocześnie płaski stan odkształcenia; przykład: tarcza. Naprężenia główne - ekstremalne naprężenia normalne, uzyskane w wyniku rozwiązania zagadnienia wartości własnych dla tensora naprężenia.

ANALIZA WRAŻLIWOŚCI. Analiza wrażliwości to analiza, która opiera się na przewidywaniu wyniku, przy zastosowaniu zmiennych układów mających wpływ na wyniki. Dotyczy ona głównie ustalania wrażliwości opłacalności danego przedsięwzięcia na zmiany parametrów wejściowych danego modelu ekonomicznego. Stanowi ważne narzędzie redukcji ryzyka decyzji podejmowanych w gospodarce rynkowej, zwłaszcza dotyczących zyskowności inwestowania. Głównym zadaniem analizy wrażliwości jest obliczanie punktu zwrotnego, który oznacza zrównanie się kosztu sprzedawanego wyrobu z dochodami. Analiza ta pozwala obliczyć graniczny poziom zastosowania poszczególnych czynników, które zapewniają osiągnięcie określonego progu rentowności. Może być ona stosowana dla rozważenia potencjalnego wpływu różnych struktur cen i kosztów, które mogą być związane z różnymi systemami produkcji lub operacji.

BADANIA WYTRZYMAŁOŚCIOWE (TWARDOŚĆ, TENSOMETRIA). Twardością określa się odporność materiału na odkształcenia trwałe, które powstają pod wpływem sił skupionych, działających na małą powierzchnię materiału, wywołanych przez wciskanie odpowiedniego wgłębnika. Twardość nie jest stałą materiałową, a więc porównywanie twardości jest możliwe w zakresie tylko jednej metody. W zależności od wielkości odkształcenia spowodowanego wnikaniem wgłębnika w materiał rozróżnia się pomiary makro- i mikrotwardości. Ważne jest aby miejsce, w którym dokonywany będzie pomiar, zostało oszlifowane, ponieważ stan powierzchni metalu ma duży wpływ na wyniki uzyskane podczas badań twardości. Do pomiarów makrotwardości stosuję się metody: Brinella, Vickersa, Rockwella. Metoda Vickersa polega na wciskaniu wgłębnika (najczęściej zrobionego ze spieków choć zdarzają się również diamentowe) o kształcie ostrosłupa prawidłowego w próbkę metalu. Twardość wyznacza się ze stosunku siły obciążającej wgłębnik F do powierzchni pobocznicy odcisku. Metoda Rokwella polega na dwustopniowym wciskaniu (przy określonych warunkach) w badaną próbkę wgłębnika w kształcie kulki stalowej (skala B, T, F) lub stożka diamentowego o kącie rozwarcia 120 stopni (skala C, A). Miarą twardości w metodzie Rockwella jest różnica pomiędzy stałą wartością K a głębokością odcisku h. Tensometria - punktowa metoda pomiarów odkształceń materiału badanej konstrukcji, pozwalająca na wyznaczenie odkształceń wybranych punktów powierzchni obiektu, za pomocą tensometrów przyklejonych w tych punktach. Najczęściej stosowanym typem tensometrów są tensometry elektrooporowe, wykorzystujące zjawisko liniowej zależności zmiany oporu od odkształcenia i pozwalające na określenie odkształceń zarówno statycznych jak i dynamicznych. Tensometry elektrooporowe można stosować w miejscach trudnodostępnych i cechują się one dużą dokładnością. Ich wadą jest jednak stosunkowo duża cena w połączeniu z jednorazowością zastosowania, a także możliwość odklejenia od powierzchni obiektu co może sprawić, że odkształcenia mierzone przez niektóre tensometry mogą znacznie odbiegać od wartości rzeczywistych. Jest to wysoce prawdopodobne w przypadku złożonego eksperymentu, w którym wykorzystuje się dużą liczbę tensometrycznych punktów pomiarowych.

CHARAKTERYSTYKA WM JAKO CIAŁA ODKSZTAŁCALNEGO. Część mechaniki o praktycznym, inżynierskim charakterze. W rozwiązaniu zadań wykorzystuje się uproszczenia i uogólnienia. Dzięki temu obiekt zostaje przekształcony w model, który umożliwia rozwiązanie problemu.

CZYSTE ZGINANIE. Czystym zginaniem nazywamy odkształcenie belki pomiędzy dwiema parami sił o równych momentach.

DOŚWIADCZALNE PODSTAWY WM. Podstawowym doświadczeniem w wytrzymałości materiałów jest statyczna próba rozciągania. Znaczenie tej próby dla wytrzymałości jest ogromne, ponieważ: określa związek pomiędzy naprężeniami i odkształceniami (prawo Hooke'a); dostarcza podstawowych informacji o właściwościach wytrzymałościowych materiałów. Statyczna próba rozciągania polega na rozciąganiu znormalizowanej próbki z określoną, niewielką prędkością i rejestracji siły rozciągającej oraz wydłużenia próbki. Fazy w rozciąganiu próbki: a) zakres odkształceń sprężystych (obowiązuje prawo Hooke'a); b) odkształcenia trwałe, plastyczne; c) górna granica plastyczności (siła rozciągająca przestaje wzrastać, a nawet zaczyna się zmniejszać z jednoczesnym przyrostem wydłużenia - płynięcie materiału); d) umocnienie materiału (dalszy wzrost obciążenia, wyraźne obciążenia plastyczne); e) pojawienie się wyraźnego przewężenia - szyjki (maksymalne obciążenie); f) pozorne zmniejszenie siły rozciągającej (ponieważ szyjka powoduje zmniejszenie pola przekroju próbki) i zerwanie próbki. g) Przerwanie wzrostu obciążenia i powolne odciążenie próbki.

EKONOMICZNE ASPEKTY OBLICZEŃ WYTRZYMAŁOŚCIOWYCH. Odpowiednia wiedza teoretyczna i praktyczna w obszarze danego zagadnienia inżynierskiego. Umiejętność postrzegania swojego działania i jego skutków w szerokim aspekcie, również ekonomicznym (podejście systemowe). Uwzględnianie faktu, że dzisiaj podejmowane decyzje skutkują w często nieprzewidzianej przyszłości, w nieokreślonym miejscu. Nabycie umiejętności podejmowania decyzji kompromisowych z uwzględnieniem ryzyka. Stosowanie w pracy metod optymalnego projektowania. Wykorzystywanie najnowszych osiągnięć naukowych i technicznych w zakresie projektowania, nowych materiałów i technologii.

GŁÓWNE MOMENTY BEZWŁADNOŚCI. to wartości ekstremalne jakie osiągają momenty bezwładności obliczone względem głównych osi bezwładności. Główne centralne momenty bezwładności opisuje wzór: I_1,2 = [I_X + I_Y]/2 +- Ѵ[(I_x - I_Y/2)² + I²_XY]; I₁ = I_MAX > I₂ = I_min

MES. Metoda elementów skończonych polega na odejściu od ciągłego modelu konstrukcji na rzecz jej podziału na skończoną liczbę ściśle zdefiniowanych elementów - elementów skończonych. Podział konstrukcji na elementy nazywa się dyskretyzacją konstrukcji, która ciągły model obliczeniowy zastępuje pewną skończoną liczbą elementów. Praktyczne stosowanie MES wymaga przede wszystkim dogłębnej znajomości wytrzymałości materiałów, jak również podstaw metod numerycznych i znajomości technik komputerowych. Jedną z najważniejszych czynności mających wpływ na końcowy wynik jest właściwy podział konstrukcji na odpowiednio dobrane elementy. Wymaga to umiejętności analizowania rozkładów naprężeń i przemieszczeń w konstrukcji oraz formułowania warunków brzegowych. MES jest więc procesem polegającym na utworzeniu pewnego, olbrzymiego układu równań, opisującego w przybliżony sposób zmiany poszukiwanych wielkości na podstawie skończonego, dyskretnego zbioru danych wejściowych. Zakres zastosować MES: określanie rozkładów przemieszczeń i naprężeń w konstrukcjach; określanie rozkładów temperatur; badanie koncentracji naprężeń; określanie częstości i postaci drgań własnych i wymuszonych; analiza propagacji pęknięć (szczelin zmęczeniowych); optymalizacja kształtu konstrukcji. Współczesne zadania inżynierskie są rozwiązywane przez odpowiednio przygotowane systemy komputerowe. Każdy system komputerowy (ALGOR, COSMOS) składa się z trzech zasadniczych części: - preprocesora, umożliwiającego graficzne wprowadzanie danych wejściowych, dyskredytację konstrukcji (automatyczną), procesora, rozwiązującego z wymaganą dokładnością olbrzymie układy równań algebraicznych, obliczającego poszukiwane wielkości we wszystkich węzłach, postprocesora, przedstawiającego w zwartej postaci otrzymane wyniki.

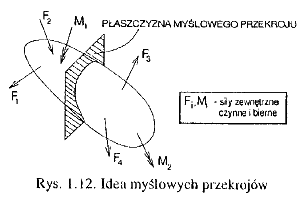
METODA MYŚLOWYCH PRZEKROJÓW. ZASADY OKREŚLANIA MYŚLOWYCH PRZEKROJÓW. Zasada myślowych przekrojów polega na dokonaniu myślowego przekroju konstrukcji i myślowego rozdzielenia ciała na dwie części. Dzięki temu ujawniają się siły wewnętrzne, które muszą być w równowadze z siłami zewnętrznymi działającymi na daną część ciała. Kierunki sił wewnętrznych w obu częściach myślowego przekroju są przeciwnie skierowane, gdyż po „złożeniu” przekroju suma sił wewnętrznych musi być równa zeru. [rys 1.12 i 1.14]

METODA PARAMETRÓW POCZĄTKOWYCH. Wykorzystanie metody parametrów początkowych w praktycznych obliczeniach wymaga wykonania następujących czynności: - wyznaczenia momentu zginającego dla ostatniego przedziału wydzielonego na długości belki; - ułożenie równania różniczkowego linii ugięcia; - scałkowanie równania linii ugięcia; otrzymuje się równanie kątów obrotów; - scałkowanie równania kątów obrotów; otrzymuje się równanie ugięć.

MODELOWANIE W WM. Model to abstrakcyjny obiekt zastępujący w reprezentatywny sposób inny ze względu na potrzebę. WM posługuje się modelem ciała jednorodnego, izotropowego, idealnie sprężystego, w którym materiał wypełnia objętość ciała w sposób ciągły. Umożliwia stosowanie w rozwiązaniu inżynierskich pojęć i aparatu analizy matematycznej. Model musi zachowywać istotne dla rozwiązywanego problemu cechy i właściwości rzeczywistego obiektu. Typy konstrukcji: modele podstawowe proste: pręt prosty (rozciąganie, ściskanie), wał (ściskanie), belka (zginanie); modele złożone: pręt cienkościenny, płyta, powłoka walcowa, powłoka; Model nominalny - wiernie przedstawiający badany fragment rzeczywistości. Model matematyczny - jednoznacznie odpowiada modelowi nominalnemu, powinien być możliwie prosty i łatwy w rozwiązaniu, może przybrać postać schematu obliczeniowego.

NAPRĘŻENIA DOPUSZCZALNE. WARUNEK WYTRZYMAŁOŚCIOWY. Naprężenia, które mogą występować w materiale bez obawy naruszenia warunku wytrzymałości i warunku sztywności, nazywamy naprężeniami dopuszczalnymi. Oznaczamy je literą k z odpowiednim indeksem dolnym, charakteryzującym rodzaj odkształcenia: r - naprężenie dopuszczalne przy rozciąganiu, c - naprężenie dopuszczalne przy ściskaniu, g - naprężenie dopuszczalne przy zginaniu, t - naprężenie dopuszczalne przy ścinaniu, s - naprężenie dopuszczalne przy skręcaniu. Rozróżniamy dwa rodzaje prostych stanów naprężeń: naprężenia normalne, w których obciążenie oddziałuje w kierunku prostopadłym do rozpatrywanego przekroju. Naprężenia normalne są zwyczajowo oznaczane symbolem „s” (sigma) wraz z indeksem odpowiadającym rodzajowi naprężeń. naprężenia styczne, w których obciążenie oddziałuje równolegle do rozpatrywanego przekroju. Naprężenia styczne są zwyczajowo oznaczane symbolem „t” (tau). Warunek wytrzymałościowy naprężeń normalnych na rozciąganie, lub ściskanie ma postać: σ = F/S <= k; gdzie: σ - naprężenia normalne w [Pa]; F - siła w [N]; S - przekrój na który działa siła F wyrażony w [m2]; k - naprężenia dopuszczalne na rozciąganie (kr), ściskanie (kc) w [Pa]; Warunek wytrzymałościowy naprężeń normalnych na zginanie ma postać: σ_g = M/W_x <= k_g; gdzie: sg - naprężenia normalne zginające w [Pa]; M - moment zginający przekrój w [Nm]; Wx - wskaźnik wytrzymałości przekroju na zginanie [m3]; kg - naprężenia dopuszczalne na zginanie w [Pa]; Warunek wytrzymałościowy naprężeń stycznych na ścinanie ma postać: τ_t = F/S <= k_t; gdzie: τt - naprężenia styczne w [Pa]; F - siła w [N]; S - przekrój na który działa siła F wyrażony w [m2]; kt - naprężenia dopuszczalne na ścinanie w [Pa]; Warunek wytrzymałościowy naprężeń stycznych na skręcanie ma postać: τ_s = M/W_o <= k_s; gdzie: ts - naprężenia styczne skręcające w [Pa]; M - moment skręcający przekrój w [Nm]; Wo - wskaźnik wytrzymałości przekroju na skręcanie [m3]; ks - naprężenia dopuszczalne na skręcanie w [Pa];

NAPRĘŻENIA TERMICZNE I MONTAŻOWE W UKŁADACH PRĘTOWYCH. NAPRĘŻENIA TERMICZNE Pod wpływem zmian temperatury elementy konstrukcyjne zmieniają swoje wymiary. Zmianę długości pręta można obliczyć z następującej zależności: ΔL_t = αLΔT. Współczynnik rozszerzalności liniowej α jest cechą charakterystyczną materiału odczytywaną z tabeli wartości liczbowych współczynników rozszerzalności. Pręt poddany działaniu temperatury, będący elementem układu prętów, oddziałuje na sąsiednie pręty. Całkowite odkształcenie pręta jest sumą odkształcenia termicznego i odkształcenia sprężystego, wywołanego siłami powstałymi na skutek oddziaływania sąsiadujących prętów. NAPRĘŻENIA MONTAŻOWE Poszczególne elementy dużych, złożonych konstrukcji są wykonywane z odchyłkami wymiarowymi, założonymi przez konstruktora. W wyniku niekorzystnego zbiegu okoliczności suma tych odchyłek może spowodować powstanie luzu montażowego, który w czasie montażu musi być „zlikwidowany” przez działanie sił umożliwiających zmontowanie konstrukcji. Powoduje to powstanie dodatkowych naprężeń, zwanych naprężeniami montażowymi. W krańcowym przypadku konstrukcja mająca spełniać określone zadania (np. przenosić obciążenia) już w czasie montażu może ulec zniszczeniu. Najczęściej spotykaną przyczyną luzów montażowych jest nieprzestrzeganie ustalonych warunków konstrukcyjnych i technologicznych w wyniku lekceważenia zasad sztuki inżynierskiej. Należy też wspomnieć, Że w pewnych sytuacjach wywołanie naprężeń wstępnych jest działaniem celowym, np. w połączeniach śrubowych naciąg wstępny zapobiega odkręcaniu się nakrętek, a w połączeniach kołnierzowych zapewnia szczelność połączenia. Naprężenia montażowe mogą osiągnąć spore wartości, tak Że po dodaniu obciążenia zapas wytrzymałościowy może być już niewielki.

NAPRĘŻENIA. ZWIĄZKI POMIĘDZY NAPRĘŻENIAMI I SIŁAMI WEWNĘTRZNYMI. [rys. 1.18] Naprężeniem w punkcie nazywa się wektor zdefiniowany zależnością: σ = lim ΔN/ΔA = dN/dA. Kierunek wektora zdefiniowanego jest taki sam jak wektora ΔN. Jednostką naprężenia jest paskal [Pa]. 1MPa = 10⁶Pa. ZWIĄZKI: równania statyki można formułować tylko dla sił. W równaniach równowagi dla przestrzennego układu sił występują siły σ_xdA, τ_xydA, τ_xzdA. Dla sześciu równań statyki otrzymuje się: P = ʃ_A σ_xdA; T_y = ʃ_A τ_xydA; T_z = ʃ_A τ_xzdA; M_x = ʃ_A (τ_xzy - τ_xyz)dA; M_y = ʃ_A σ_xdA; M_z = -ʃ_A σ_xydA; Naprężenia normalne σ: rozciąganie prętów N, zginanie w płaszczyźnie pionowej M_Z, zginanie w płaszczyźnie poziomej M_Y; Naprężenia styczne τ_xy, τ_xz: ścinanie T_Y, ścinanie T_Z, skręcanie M_XY.

OBCIĄŻENIA PROSTE W WM. OBCIĄŻENIA ZŁOŻONE. Obciążenia proste: rozciąganie (ściskanie), ścinanie, skręcanie, zginanie; Obciążenia złożone: kombinacje wyżej wymienionych przypadków. Cecha charakterystyczna WM.

ODKSZTAŁCENIA, PRZEMIESZCZENIA. RODZAJE ODKSZTAŁCEŃ: liniowe, które są określane jako wektor o początku w pewnym punkcie ciała nieodkształconego i końcu w tym samym punkcie ciała odkształconego; kątowe, które są określane za pomocą kąta zawartego pomiędzy dowolnie krótkim odcinkiem związanym z rozpatrywanym ciałem przed odkształceniem i po jego odkształceniu. Przemieszczenia ciała są wynikiem odkształceń.

OGÓLNY PRZYPADEK WYTRZYMAŁOŚCI ZŁOŻONEJ. Przykładem ogólnego przypadku wytrzymałości złożonej mogą być przestrzenne konstrukcje prętowe obciążone siłami skupionymi, obciążeniami ciągłymi oraz momentami. Na skutek zmiany kierunku osi pręta zmienia się charakter siły wewnętrznej wywołanej przez daną siłę zewnętrzną. W tej sytuacji bardzo ważnym elementem rozwiązywania zadania jest kontrolowanie ciągłości wykresów sił wewnętrznych wywołanych przez dane obciążenie - od punktu przyłożenia aż do utwierdzenia, przy czym np. moment zginający pewien odcinek pręta na sąsiednim prostopadłym odcinku staje się momentem skręcającym. Wykorzystując warunki wytrzymałościowe w celu obliczenia średnicy pręta lub dopuszczalnych obciążeń, należy pomijać naprężenia styczne wywołane siłami poprzecznymi. W wielu przypadkach w tzw. obliczeniach wstępnych pomija się również naprężenia normalne pochodzące od sił rozciągających lub ściskających. W warunku wytrzymałościowym uwzględnia się wówczas tylko momenty zginające i skręcające, dlatego należy obowiązkowo wykonać obliczenia sprawdzające, uwzględniając wszystkie siły wewnętrzne. W przestrzennych konstrukcjach prętowych znaczenia nabiera sprawa określania znaków sił wewnętrznych. Założenia stosowane przy zginaniu płaskim tracą tutaj swoje znaczenia. Najczęściej przyjmuje się, że momenty zginające rysuje się po ściskanej stronie pręta. W przypadku momentów skręcających należy zaznaczać znaki dla rozróżnienia momentów działających w przeciwnych kierunkach. Sprawa znaków jest istotna, ponieważ z uwagi na warunek wytrzymałościowy należy w niebezpiecznych przekrojach konstrukcji prawidłowo sumować wartości sił i momentów.

PRAWO HOOKE'A DLA JEDNOOSIOWEGO ROZCIĄGANIA. UOGÓLNIONE PRAWO HOOKE'A I JEGO ZNACZENIE. Prawo Hooke'a - prawo mechaniki określające zależność odkształcenia od naprężenia. Głosi ono, że odkształcenie ciała pod wpływem działającej na niego siły jest wprost proporcjonalne do tej siły. Współczynnik między siłą a odkształceniem jest często nazywany współczynnikiem (modułem) sprężystości. Prawo Hooke'a zakłada też, że odkształcenia ciała, w reakcji na działanie sił, następują w sposób natychmiastowy i całkowicie znikają, gdy przyłożone siły przestają działać. Takie uproszczenie jest wystarczające jedynie dla ciał o pomijalnie małej lepkości. Związki między odkształceniami i naprężeniami, w przypadku ciała izotropowego, opisuje uogólnione prawo Hooke'a.

RACHUNEK JEDNOSTEK. ZASADY, ZASTOSOWANIA. Rachunek jednostek jest sporządzany by sprawdzić poprawność wykonanych obliczeń. Liczymy z podanego wzoru jakieś zadanie i powinien nam wynik wyjść w odpowiednich dla danej wartości jednostkach. Wtedy właśnie stosujemy ten rachunek jednostek czyli rozpisujemy po kolei do ostatecznych jednostek z układu SI dane jednostki (np. Newtony, Dżule itp. na sekundy, metry itd.), skracamy co się da i gdzie się da, a potem sprawdzamy czy dają w sumie jednostkę taką, jaka miała wyjść. Rachunek ten wydaje mi się bardzo ważny ponieważ pozwala sprawdzić poprawność wykonanych obliczeń, i właśnie do tego się go stosuje. mega (M) → 10^6 → 1000000; kilo (K) → 10^3 → 1000; centy (c) → 10^-2 → 0,01; mili (m) → 10^-3 → 0,001; mikro ()→ 10^-6 → 0,000001;

RÓWNANIE RÓŻNICZKOWE LINII UGIĘCIA. Jest wyprowadzone z dwóch wzorów: 1. Równanie osi odkształconej belki dla czystego zginania: 1/ρ = -M / EI_Z; 2. Wzór na promień krzywizny po uproszczeniu: 1/ρ = +- y^'' / [1+(y^')²]^3/2 ≈+- d²y / dx²; gdzie(y^')² ≈ 0; Równanie to ma postać: d²y/dx² = +- M/EI_Z; Analityczna metoda wyznaczania przemieszczeń polega na bezpośrednim całkowaniu równania różniczkowego linii ugięcia, niestety dla belek z większą liczbą przedziałów (dużo częściej spotykanych) jest ona strasznie pracochłonna i czasochłonna to jej zastosowanie w praktyce jest bardzo małe.

SIŁA - DEFINICJE, KLASYFIKACJE. Siła jest to wynik wzajemnego mechanicznego oddziaływania na siebie co najmniej dwóch ciał. Oddziaływania te przejawiają się przez wyprowadzenie ciała ze stanu spoczynku lub zmianę parametrów ruchu ciała już poruszającego się. Siła jest wektorem umiejscowionym, stąd do określenia jej wartości potrzebna jest znajomość wartości liczbowej, kierunku działania i zwrotu. KLASYFIKACJE: zewnętrzne - siły przyłożone do punktów materialnych rozpatrywanego układu, wywierane przez inny układ punktów materialnych; wewnętrzne - siły wzajemnego oddziaływania między punktami materialnymi w rozpatrywanym układzie; skupione - przyłożone do punktu geometrycznego (mała powierzchnia w stosunku do ciała); rozłożone - powierzchniowe: rozłożone na całej powierzchni ciała materialnego lub jej części; objętościowe: rozłożone w całej objętości; rozłożone wzdłuż linii;

SIŁY ZEWNĘTRZNE CZYNNE I BIERNE. SIŁY WEWNĘTRZNE. Siły zewnętrzne: czynne (obciążenia) - siły skupione, rozłożone liniowo i momenty; bierne (reakcje) - siły skupione, momenty; Siły wewnętrzne: są wynikiem oddziaływania jednej części ciała oddzielonej myślowym przekrojem na drugą.

SPOSÓB CLEBSCHA. Wymaga przestrzegania kilku reguł podczas wyznaczania momentu zginającego: a) lewy koniec belki jest początkiem układu współrzędnych XY; b) Równanie momentów zginających pisze się dla ostatniego, prawego przedziału belki. W ten sposób do każdego kolejnego przedziału wchodzą składniki równania z przedziału poprzedniego.; c) W przypadku działanie momentu skupionego M w równaniu momentów uwzględnia się współrzędną tego momentu w postaci M(x-a)0. d) Obciążenie ciągłe działające na pewnej długości belki należy doprowadzić do końca belki z jednoczesnym dodaniem na uzupełnionym odcinku równoważnego obciążenia ciągłego o przeciwnym znaku. e) Całkowanie wyrazów zawierających dwumian (x-a) należy wykonywać bez otwierania nawiasów, tzn. ʃ(x-a)ⁿ dx = ʃ(x-a)ⁿ d(x-a) = (x-a)ⁿ⁺¹ / n+1 + C.

ŚRODKI CIĘŻKOŚCI I MOMENTY STATYCZNE FIGUR PŁASKICH. Do określenia położenia środka ciężkości przekrojów złożonych powszechnie wykorzystuje się podział przekroju na figury płaskie. Po dokonaniu podziału współrzędne środka ciężkości określa się z zależności: x_c = [ΣA_ix_i / ΣA_i]; y_c = [ΣA_iy_i / ΣA_i]; Moment statyczny figur płaskich to moment powierzchniowy pierwszego rzędu. Definiuje go się następująco: S_x = ʃ_A ydA; S_y = ʃ_A xdA; gdzie A - pole powierzchni przekroju, dA - powierzchnia elementarna.

TWIERDZENIE STEINERA. Momenty osiowe oraz biegunowe są zawsze dodatnie, natomiast moment dewiacyjny może być dodatni lub ujemny. TWIERDZENIE STEINERA: Osiowy moment bezwładności figury płaskiej względem osi równoległej odległej od środka ciężkości o określoną wartość jest równy momentowi względem osi równoległej przechodzącej przez środek ciężkości figury, powiększonemu o iloczyn powierzchni figury i kwadratu odległości między osiami. Moment dewiacyjny figury płaskiej względem Si równolegle przesuniętych jest równy momentowi dewiacyjnemu względem osi centralnych, powiększonemu o iloczyn powierzchni i obu składowych równoległego przesunięcia. MATEMATYCZNIE: I_X = I_X0 + Aa²; I_Y = I_Y0 + Ab²; I_XY = I_X0Y0 + Aab;

UKŁADY PRĘTOWE. Siły wewnętrzne w pręcie wyznacza się za pomocą metody przekrojów. Myślowych przekrojów należy dokonywać w dowolnych miejscach odcinków, których granicami są punkty przyłożenia obciążenia oraz zmiany kształtu poprzecznego pręta ( np. wielkości przekroju). Równanie równowagi: suma sił działających wzdłuż osi pręta jest równa zeru. Zadania statycznie niewyznaczalne charakteryzują się tym, że liczba niewiadomych jest większa od liczby równań statyki. Rozwiązanie zadania statycznie niewyznaczalnego wymaga ułożenia dodatkowych równań geometrycznych. Równania geometryczne buduje się wykorzystując zasadę nierozdzielności konstrukcji, polegającą na tym, że odkształcona konstrukcja stanowi w dalszym ciągu jedną całość i tym samym odkształcenia jej wszystkich elementów są ze sobą powiązane poprzez istnienie więzów (przegubów). Równania geometryczne wykorzystując ten fakt są równaniami zawierającymi odkształcenia wszystkich elementów RG = f(_li). Przy wykorzystaniu prawa fizycznego (prawo Hooke'a), równanie geometryczne przekształca się tak, że występują w nim siły wewnętrzne, czyli RG = f(Si). Równania w tej postaci mogą razem z równaniami statyki tworzyć układ pozwalający na rozwiązanie zadania.

WIĘZY, REAKCJE. Więzy są to warunki ograniczające swobodę poruszania się ciał. Najczęściej są to warunki geometryczne, pozwalające na podział ciał na swobodne i nieswobodne. Reakcje są to siły bierne stanowiące wynik oddziaływania więzów i zależą od warunków w jakich znajduje się dane ciało. Rodzaje więzów: Podpory ruchome. Należą do nich: podparcie na idealnie gładkiej powierzchni, podparcia na ostrzu, pryzmacie i podparcia w łożysku ruchomym. Reakcja podpory ruchomej jest zaczepiona w punkcie styczności ciała z podporą i ma zawsze kierunek prostopadły do powierzchni podpieranej (niezależnie od kierunków sił działających na ciało podpierane). Podporę ruchomą oznaczamy schematycznie za pomącą trójkąta równobocznego dodatkowo podkreślonego linią, która przedstawia powierzchnię podpierająca. Więzy wiotkie. Zaliczamy tu sznury, liny, łańcuchy itp. Siła w takich więzach jest zawsze skierowana wzdłuż osi tych więzów. Podpora ruchoma i więzy wiotkie należą do więzów charakteryzujących się jedną niewiadomą podporową. W więzach tych znamy kierunek i punkt zaczepienia reakcji. Jedną niewiadomą jest wartość reakcji (zwrot reakcji, jak zauważymy na przykładach, otrzymamy w toku obliczania jej wartości). Podpora stała. Tego rodzaju więzy uniemożliwiają przesunięcie ciała, lecz umożliwiają obrót wokół punktu podparcia.

WŁASNOŚCI MECHANICZNE MATERIAŁÓW KONSTRUKCYJNYCH. Własności mechaniczne materiałów konstrukcyjnych, są to cechy związane z wytrzymałością materiału na działanie różnego rodzaju sił zewnętrznych, są kryterialnymi wielkościami w doborze materiałów. Poznanie własności materiałów nie jest wystarczające do oceny ich przydatności do określonego celu. Niezbędne jest tu jeszcze poznanie wpływu różnych czynników, np. temperatury, czasu, sposobu i wielkości obciążenia, kształtu i wymiarów przedmiotu, na zmiany tych własności. Metody badań własności mechanicznych możemy podzielić na dwie grupy: - własności technologiczne, decydujące o przydatności materiałów do określonej obróbki; - własności wytrzymałościowe, do wyznaczania, których niezbędna jest znajomość siły lub momentu sił, jako jednej z wielkości mierzonych podczas badania. Wyniki badań są wykorzystywane przez konstruktorów w procesie projektowania elementów konstrukcyjnych.

WSPÓŁCZYNNIK BEZPIECZEŃŚTWA. ZNACZENIE EKONOMICZNE WSPÓŁCZYNNIKA BEZPIECZEŃSTWA. Współczynnik bezpieczeństwa jest to liczba większa od jedności mówiąca ile razy wielkość dopuszczalna jest mniejsza od wielkości uznawanej za niebezpieczną. Stosowany jest do naprężeń obciążeń i stanowi przedmiot szeregu norm, szczególnie duże wartości osiąga w obliczeniach stateczności. Współczynnik bezpieczeństwa jest zmienny i wynosi od 1,5 do 3 dla materiałów plastycznych i od 8 do 12 dla materiałów kruchych, uwzględnia wartości technologiczne, warunki pracy i dopuszczalne błędy. Warunki współczynników bezpieczeństwa: jednorodność materiału; jakość wykonania; naprężenia wstępne w czasie procesu technologicznego np. kucia, odlewu, spawania; obciążenia przewidywane i przypadkowe; czynnik niedoskonałości ludzkiej; niedoskonałość metod obliczeniowych; wpływ czasu pracy; procesy korozji, ścierania, wietrzenia; zmęczenie materiału; spiętrzenie naprężeń.

WYBOCZENIE KONSTRUKCJI. Wyboczenie jednego elementu pociąga za sobą zazwyczaj lawinowe zniszczenie powiązanych elementów. Utrata stateczności była przyczyną wielu głośnych katastrof budowlanych, takich jak zawalenia się budynków, mostów czy masztów radiowych. Przy projektowaniu konstrukcji prętowych, płyt, powłok itp. kryterium stateczności konstrukcji jest głównym kryterium wytrzymałościowym, spychającym na dalsze miejsce kryterium naprężeniowe i sztywnościowe. Badanie stateczności konstrukcji porównuje się z sytuacją kulki znajdującej się w polu grawitacyjnym (polu przyciągania ziemskiego): Dowolnie małe wychylenie kulki (zakłócenie) znajdującej się w najniższym punkcie wklęsłej powierzchni spowoduje zmianę jej położenia i powrót do położenia początkowego - stan kulki można określić jako równowagę stałą. Kulka znajdująca się w najwyższym punkcie powierzchni wypukłej teoretycznie znajduje się w równowadze, lecz jest to równowaga niestała (chwiejna), praktycznie nie do zrealizowania. Kulka znajdująca się na powierzchni płaskiej znajduje się w stanie określanym jako równowaga obojętna, gdyż jej stan jest taki sam w każdym miejscu na płaszczyźnie.

WYTĘŻENIE. HIPOTEZY WYTRZYMAŁOŚCIOWE. HIPOTEZY MAX. NAPRĘŻENIA STYCZNEGO. HIPOTEZA HUBERA. Wytężenie materiału - stan materiału obciążonego siłami zewnętrznymi, w którym istnieje niebezpieczeństwo przejścia w stan plastyczny - przekroczenie granicy sprężystości, jeśli materiał taką posiada - lub utrata spójności (pękniecie, przełom, dekohezja). Wytężenie materiału określa się przez redukcję złożonego stanu naprężenia do jednego naprężenia zredukowanego lub zastępczego. To naprężenie może być porównane z podstawowymi wytrzymałościowymi stałymi materiałowymi wytrzymałością na rozciąganie Rm lub naprężeniem rozrywającym Ru, które uzyskuje się w czasie statycznej próby rozciągania. Do redukcji złożonego stanu naprężenia stosuje się hipotezy wytężeniowe. Najczęściej stosowana jest hipoteza energii odkształcenia (sformułowana przez polskiego uczonego Maksymiliana T. Hubera), która zakłada, że ciało jest doskonale sprężyste, i że praca naprężenia zredukowanego równa jest sumie prac wszystkich naprężeń składowych: Hipoteza maksymalnego naprężenia stycznego przyjęta przez Coulomba, mówi o tym, że miarą wytężenia materiału jest największe natężenie styczne. Spośród hipotez ogólnych, dających wyniki zgodne z doświadczeniem, należy wymienić hipotezę energii odkształcenia postaciowego (hipotezę Hubera). miarą wytężenia materiału jest wartość energii sprężystej odkształcenia postaciowego. Hipoteza Hubera jest potwierdzona doświadczalnie i jest obecnie bardzo szeroko stosowana w praktyce inżynierskiej.

WYTRZYMAŁOŚĆ ZŁOŻONA - ZGINANIE UKOŚNE, ZGINANIE I ROZCIĄGANIE (RDZEŃ PRZEKROJU), ZGINANIE I SKRĘCANIE. Zginanie ukośne (zginanie złożone) jest bezpośrednio związane ze zginaniem prostym. Występuje wówczas, gdy wektor momentu zginającego belkę nie pokrywa się z kierunkiem żadnej z osi symetrii. Zginanie ukośne można traktować jako sumę zginania prostego w płaszczyźnie pionowej oraz w płaszczyźnie poziomej. Wspólne działanie sił rozciągających (ściskających) oraz momentu zginającego występuje najczęściej przy mimośrodkowym obciążeniu pręta. Mimośrodkowość może być wywołana przyłożeniem sił poza środkiem ciężkości, wykrzywieniem osi pręta lub równocześnie dwoma tymi czynnikami. Wspólne działanie zginania i skręcania jest najczęściej spotykanym przypadkiem wytrzymałości złożonej. W ten sposób są obciążone wały maszyn, pojazdów, skrzyni biegów itp. Ten rodzaj wytrzymałości złożonej charakteryzuje się niejednorodnym rozkładem naprężeń - moment zginający powoduje powstanie naprężeń normalnych, moment skręcający naprężeń stycznych (rysunek).

ZADANIA STATYCZNIE NIEWYZNACZALNE. Stopień statycznej niewyznaczalności - różnica pomiędzy ilością niewiadomych a liczbą równań statyki. Równań statyki zazwyczaj jest trzy, dlatego dla przykładu gdy mamy trzy równania z pięcioma niewiadomymi to stopień statycznej niewyznaczalności (SSN) jest równy 2 (5-3=2). Równania geometryczne buduje się wykorzystując zasadę nierozdzielności konstrukcji, polegającą na tym, że odkształcona konstrukcja stanowi w dalszym ciągu jedną całość i tym samym odkształcenia jej wszystkich elementów są ze sobą powiązane poprzez istnienie więzów (przegubów).

ZASADA DE SAINT-VENANTA. Jeśli na sprężyste ciało działa układ sił statycznych przyłożonych na powierzchni małej w stosunku do powierzchni całego ciała i zastąpimy ten układ sił dowolnym innym układem - jednak statycznie mu równoważnym (o równej sumie układu i sumie momentów sił układu względem dowolnego punktu) - to istnieje taki przekrój tego ciała, dostatecznie odległy od miejsca przyłożenia sił, że różnice w naprężeniach, odkształceniach i przemieszczeniach, pochodzących od obu przypadków obciążenia, są dowolnie małe (tzn. wpływ działających sił uśrednia się). Ilustracją zasady jest rysunek. Pokazuje on pręt rozciągany przez siły przyłożone punktowo w środku ciężkości przekroju na obu końcach. W bezpośredniej bliskości końców stan naprężenia odpowiada rzeczywistemu stanowi obciążenia. W dostatecznej odległości od końców uśrednia się i równy jest sumie sił podzielonej przez pole przekroju pręta.

ZASADA SUPERPOZYCJI. Gdy między przyczyną a skutkiem zachodzi liniowa zależność, można rozpatrywać skutki kilku przyczyn występujących równocześnie jako sumę skutków przyczyn działających pojedynczo i oddzielnie. Rezultaty działania kilku sił są równe sumie (algebraicznej lub geometrycznej) rezultatów, otrzymywanych w wyniku działania kaŻdej siły oddzielnie.

ZASADY STATYKI CIAŁA SZTYWNEGO. 1.Siły działające na ciało równoważą się jeżeli wektor sił przyłożony jest na tej samej prostej, ta samą wartość i przeciwny zwrot. 2.Działanie układu się pozostanie niezmienione jeżeli + lub - dowolny układ wzajemnie równoważących się sił. 3.Dwie siły przyłożone do tego samego punktu można zastąpić jedną wypadkową siłą zgodną z zasadą równoległoboku. 4.każdemu działaniu siły towarzyszy równe co do wielkości działanie siły przeciwnej działającej w tym samym kierunku ale o przeciwnym zwrocie. 5.Równowaga sił działająca na ciało odkształcalne nie zostanie naruszona jeżeli myślowo zesztywniamy to ciało. 6.Każde ciało ograniczone więzami można myślowo oswobodzić od więzów zastępując je siłami reakcji.

ZGINANIE PŁASKIE. ZALEŻNOŚCI RÓŻNICZKOWE MIĘDZY SIŁAMI WEWNĘTRZNYMI. Zginanie płaskie: Wszystkie siły zewnętrzne czynne (obciążenia) i bierne (reakcje) leżą w jednej wspólnej płaszczyźnie przechodzącej przez oś belki. dT/dx = -q(x) oraz dM/dx = T, co nam daje równanie różniczkowe: d²M / dx² = -q(x).

ZMĘCZENIE MATERIAŁU. Zmęczenie materiału jest związane ze zmniejszeniem wytrzymałości elementów konstrukcyjnych poddanych działaniu okresowo zmiennych obciążeń. Zjawisko zmęczenia materiałów jest bardzo niebezpieczne, ponieważ zniszczenie elementu konstrukcyjnego lub części maszyny następuje nieoczekiwanie przy naprężeniach znacznie mniejszych od wytrzymałości doraźnej, wyznaczonej ze statycznej próby rozciągania. Zniszczenie następuje bez żadnych dostrzegalnych wcześniej odkształceń plastycznych. Zmęczenie materiałów ma olbrzymie znaczenie praktyczne, ponieważ większość współczesnych konstrukcji inżynierskich jest poddana działaniu zmiennych obciążeń (pojazdy, samoloty, maszyny z ruchomymi częściami). Przyczyną zmęczeniowego zniszczenia materiału jest zmienny stan naprężenia. Początek zniszczenia nastąpił w tzw. ognisku. Przyczyną zapoczątkowania procesu zmęczeniowego jest spiętrzenie naprężeń wywołane np. pęknięciem, rysą, wadą materiałową, karbem. Szczelina zmęczeniowa rozszerza się, penetruje w głąb przekroju - następuje tzw. propagacja pęknięcia. Wał ulega zniszczeniu, gdy niezniszczona część wału nie jest w stanie przenieść obciążenia. W przełomie zmęczeniowym rozróżnia się dwie strefy. Strefa zniszczenia zmęczeniowego ma wygładzoną, błyszczącą powierzchnię z charakterystycznymi liniami, w których propagacja pęknięcia została np. na skutek zmniejszenia obciążenia zahamowana. Wygładzenie tej strefy wynika z tarcia powierzchni w czasie pracy. Druga strefa nosi nazwę strefy doraźnej (resztkowej) i ma wygląd gruboziarnisty, matowy. Istnieje wiele teorii na temat powstawania ogniska i propagacji szczelin zmęczeniowych. Większość z teorii przyjmuje dyslokacje i inne wady sieci krystalicznej za przyczynę tych zjawisk.

ZNACZENIE HIPOTEZY PŁASKICH PRZEKROJÓW W WM. Przy skręcaniu wałów można napisać tylko jedno równanie statyki - sumę momentów względem osi wału. W opisie mechanizmu odkształcenia wału okrągłego wykorzystuje się tzw. hipotezę płaskich przekrojów, według której okrągłe przekroje poprzeczne wału pozostają po skręceniu płaskie i okrągłe, obracając się wokół osi wału o niewielki kąt. Hipoteza płaskich przekrojów pozwala na określenie warunków geometrycznych opisujących odkształcenia okrągłego wału. Jest ona potwierdzona doświadczalnie. Hipoteza ta znacznie ułatwia obliczanie zadań wytrzymałościowych, przy czym różnice w wynikach są naprawdę niewielkie.

---