POLITECHNIKA WARSZAWSKA
Wydział Inżynierii Środowiska
Operat hydrologiczny na potrzeby gospodarki wodnej.
Prowadzący:
mgr inż. Jerzy Brzeziński
Wykonały: Anna Starzyńska
Renata Szydlik
Spis treści:
1. Podstawowe informacje o wodowskazie
2. Krzywa przepływu la przekroju wodowskazowego
3. Przepływy charakterystyczne główne I i II rzędu oraz wykres zmienności przepływów głównych I rzędu
4. Rozkład prawdopodobieństwa przepływów rocznych minimalnych
5. Rozkład prawdopodobieństwa przepływów maksymalnych rocznych
6. Przepływy o określonym czasie trwania
7. Obliczenia wartości wybranych przepływów konwencjonalnych
1. Podstawowe informacje o wodowskazie.
wielkość powierzchni zlewni zamkniętej wodowskazem: A = 2034 km2
wodowskaz umieszczony jest na 17.8 km rzeki Tanew
rzędna zera wodowskazu: 165.54 m
Jej źródła znajdują się na zboczach najwyższego wzniesienia Roztocza, Wielkiego Działu. Tanew wypływa z bagien między wsiami Stara Huta i Złomy Ruskie, w okolicy miasteczka Narol w powiecie lubaczowskim województwa podkarpackiego.
Średni przepływ przy ujściu około 12 m3/s. Do ujścia Wirowej woda w Tanwi jest bardzo czysta.
Dla ochrony obszaru źródliskowego utworzono rezerwat "Źródła Tanwi".
Tanew płynie na północny wschód i przepływa przez Narol. Następnie opuszcza Roztocze i przecina południową część leśnego kompleksu Puszczy Solskiej. Kilka kilometrów na północ od Tanwi leży letniskowa miejscowość Susiec. Odcinek doliny Tanwi w okolicach Suśca jest objęty rezerwatem "Nad Tanwią", chroniącym unikatowe progi skalne (tzw. szumy albo szypoty) w dnie rzeki. Tam też uchodzi do Tanwi rzeczka Jeleń z najwyższym naturalnym wodospadem na Roztoczu (1,8 m). Dalej Tanew meandruje południowym skrajem Puszczy Solskiej w kierunku zachodnim, przyjmując dopływy Wirową (od południa), a od północy - Sopot i Szum. W okolicy następnej letniskowej wioski Harasiuki Tanew przyjmuje kolejny duży dopływ - Ładę. Następnie Tanew płynie przez południowy skraj Lasów Janowskich i wpada do Sanu w miasteczku Ulanów. Ujście znajduje się na wysokości 154 m n.p.m. Dolina Tanwi oddziela Równinę Biłgorajską (na północy) od Płaskowyżu Tarnogrodzkiego (na południu).
● Harasiuki
2. Krzywa przepływu dla przekroju wodowskazowego
Wyznaczanie zależności opisanej równaniem regresji II rodzaju w postaci funkcji potęgowej:
Q=ၡ(H-ၢ)n (1)
gdzie
H- stan wody [cm]
Q- natężenie przepływu [m3/s]
ၡ,n - parametry funkcji R
ၢ = Hd punkt denny
Tmax - głębokość maksymalna
ၢ śr = min(H-Tmax)
ၢ śr = 7
Parametry ၡ i n oszacowano za pomocą metody najmniejszych kwadratów poprzez zlogarytmowanie obustronnie równania (1)
lnQi =ln ၡ+n ln(Hi-ၢśr)
yi =A +n xi
Po rozwiązaniu równania dochodzimy do wzorów:
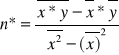
ၡ=eA
A=yśr - n*xśr
Tabela 1
ROK |
DATA |
H[cm] |
Hzm[cm] |
Q [m3/s] |
Tmax [cm] |
X |
Y |
X*Y |
X2 |
Q* |
1960 |
15.XI |
91 |
191 |
21,90 |
155 |
5,252 |
3,086 |
16,211 |
27,196 |
22,102 |
1961 |
15.III |
62 |
162 |
8,37 |
144 |
5,088 |
2,125 |
10,809 |
25,436 |
15,365 |
|
15.V |
73 |
173 |
12,90 |
139 |
5,153 |
2,557 |
13,178 |
26,132 |
17,768 |
|
29.V |
47 |
147 |
4,35 |
65 |
4,990 |
1,470 |
7,337 |
24,420 |
12,382 |
|
27.VII |
47 |
147 |
4,04 |
57 |
4,990 |
1,396 |
6,968 |
24,420 |
12,382 |
|
21.IX |
48 |
148 |
4,69 |
95 |
4,997 |
1,545 |
7,723 |
24,490 |
12,571 |
1962 |
16.IV |
63 |
163 |
13,80 |
178 |
5,094 |
2,625 |
13,369 |
25,501 |
15,575 |
|
25.V |
77 |
177 |
19,70 |
169 |
5,176 |
2,981 |
15,308 |
26,376 |
18,688 |
|
20.VII |
77 |
177 |
20,20 |
200 |
5,176 |
3,006 |
15,437 |
26,376 |
18,688 |
|
30.VIII |
29 |
129 |
6,69 |
120 |
4,860 |
1,901 |
9,131 |
23,079 |
9,249 |
|
14.IX |
27 |
127 |
5,17 |
88 |
4,844 |
1,643 |
7,865 |
22,920 |
8,931 |
|
23.IX |
32 |
132 |
6,09 |
95 |
4,883 |
1,807 |
8,723 |
23,313 |
9,738 |
|
12.X |
28 |
128 |
5,35 |
99 |
4,852 |
1,677 |
8,043 |
23,000 |
9,089 |
1963 |
19.IV |
59 |
159 |
13,20 |
115 |
5,069 |
2,580 |
12,963 |
25,239 |
14,741 |
|
24.IV |
48 |
148 |
8,57 |
100 |
4,997 |
2,148 |
10,631 |
24,490 |
12,571 |
|
13.V |
38 |
138 |
6,72 |
96 |
4,927 |
1,905 |
9,288 |
23,768 |
10,756 |
|
25.V |
33 |
133 |
5,45 |
110 |
4,890 |
1,696 |
8,200 |
23,390 |
9,904 |
|
21.VI |
29 |
129 |
4,69 |
108 |
4,860 |
1,545 |
7,424 |
23,079 |
9,249 |
|
11.VII |
24 |
124 |
3,79 |
30 |
4,820 |
1,332 |
6,345 |
22,678 |
8,464 |
|
08.VIII |
20 |
120 |
3,15 |
29 |
4,787 |
1,147 |
5,424 |
22,348 |
7,862 |
|
18.VIII |
30 |
130 |
4,54 |
35 |
4,868 |
1,513 |
7,280 |
23,157 |
9,411 |
|
19.VIII |
29 |
129 |
4,48 |
37 |
4,860 |
1,500 |
7,204 |
23,079 |
9,249 |
|
15.X |
40 |
140 |
6,28 |
48 |
4,942 |
1,837 |
8,985 |
23,916 |
11,107 |
1964 |
28.I |
156 |
156 |
3,73 |
70 |
5,050 |
1,316 |
6,587 |
25,039 |
14,131 |
|
23.II |
162 |
162 |
3,98 |
70 |
5,088 |
1,381 |
6,966 |
25,436 |
15,365 |
|
21.IV |
135 |
135 |
10,30 |
101 |
4,905 |
2,332 |
11,316 |
23,542 |
10,240 |
|
22.IV |
130 |
130 |
8,71 |
100 |
4,868 |
2,164 |
10,416 |
23,157 |
9,411 |
|
26.IV |
123 |
123 |
12,80 |
100 |
4,812 |
2,549 |
12,119 |
22,597 |
8,311 |
|
28.IV |
120 |
120 |
9,86 |
62 |
4,787 |
2,288 |
10,819 |
22,348 |
7,862 |
|
21.VI |
98 |
98 |
5,75 |
91 |
4,585 |
1,749 |
7,890 |
20,348 |
4,968 |
|
16.VII |
90 |
90 |
3,76 |
52 |
4,500 |
1,324 |
5,852 |
19,526 |
4,088 |
|
17.X |
110 |
110 |
4,72 |
43 |
4,700 |
1,552 |
7,192 |
21,481 |
6,460 |
1965 |
27.IV |
150 |
150 |
16,20 |
212 |
5,011 |
2,785 |
13,822 |
24,630 |
12,952 |
|
22.V |
120 |
120 |
6,84 |
150 |
4,787 |
1,923 |
9,090 |
22,348 |
7,862 |
|
09.VII |
122 |
122 |
8,14 |
98 |
4,804 |
2,097 |
9,949 |
22,514 |
8,160 |
|
19.VII |
158 |
158 |
19,50 |
98 |
5,063 |
2,970 |
14,903 |
25,173 |
14,536 |
|
28.VIII |
166 |
166 |
23,20 |
140 |
5,112 |
3,144 |
15,937 |
25,694 |
16,217 |
|
28.IX |
121 |
121 |
6,61 |
62 |
4,796 |
1,889 |
8,945 |
22,432 |
8,010 |
1966 |
17.II |
216 |
216 |
41,10 |
210 |
5,375 |
3,716 |
19,852 |
28,541 |
28,955 |
|
06.IV |
167 |
167 |
27,30 |
225 |
5,118 |
3,307 |
16,783 |
25,757 |
16,434 |
|
15.VI |
114 |
114 |
6,78 |
100 |
4,736 |
1,914 |
8,944 |
21,835 |
7,003 |
|
17.VII |
136 |
136 |
12,00 |
99 |
4,913 |
2,485 |
12,076 |
23,618 |
10,410 |
|
16.IX |
126 |
126 |
9,66 |
87 |
4,836 |
2,268 |
10,839 |
22,840 |
8,774 |
|
28.X |
150 |
150 |
17,00 |
97 |
5,011 |
2,833 |
14,061 |
24,630 |
12,952 |
1967 |
26.II |
254 |
254 |
98,90 |
250 |
5,537 |
4,594 |
25,311 |
30,353 |
41,260 |
|
30.V |
148 |
148 |
19,00 |
115 |
4,997 |
2,944 |
14,571 |
24,490 |
12,571 |
|
09.VI |
128 |
128 |
12,00 |
100 |
4,852 |
2,485 |
11,917 |
23,000 |
9,089 |
|
15.VII |
118 |
118 |
8,19 |
110 |
4,771 |
2,103 |
9,904 |
22,180 |
7,570 |
|
27.IX |
110 |
110 |
6,11 |
76 |
4,700 |
1,810 |
8,389 |
21,481 |
6,460 |
1968 |
10.II |
208 |
208 |
40,80 |
180 |
5,338 |
3,709 |
19,668 |
28,125 |
26,656 |
|
11.VI |
118 |
118 |
8,47 |
75 |
4,771 |
2,137 |
10,062 |
22,180 |
7,570 |
|
13.VIII |
123 |
123 |
7,32 |
80 |
4,812 |
1,991 |
9,463 |
22,597 |
8,311 |
|
18.IX |
125 |
125 |
7,77 |
87 |
4,828 |
2,050 |
9,781 |
22,759 |
8,618 |
1969 |
22.V |
126 |
126 |
10,40 |
82 |
4,836 |
2,342 |
11,192 |
22,840 |
8,774 |
|
18.VII |
110 |
110 |
6,35 |
75 |
4,700 |
1,848 |
8,567 |
21,481 |
6,460 |
1970 |
17.IX |
124 |
124 |
8,19 |
66 |
4,820 |
2,103 |
10,014 |
22,678 |
8,464 |
1971 |
08.IV |
135 |
135 |
13,30 |
111 |
4,905 |
2,588 |
12,556 |
23,542 |
10,240 |
|
21.IV |
124 |
124 |
9,66 |
110 |
4,820 |
2,268 |
10,801 |
22,678 |
8,464 |
|
15.V |
118 |
118 |
8,99 |
69 |
4,771 |
2,196 |
10,343 |
22,180 |
7,570 |
|
31.VIII |
105 |
105 |
4,55 |
68 |
4,654 |
1,515 |
6,947 |
21,022 |
5,813 |
|
16.IX |
111 |
111 |
6,16 |
86 |
4,710 |
1,818 |
8,444 |
21,570 |
6,594 |
|
13.X |
113 |
113 |
5,64 |
75 |
4,727 |
1,730 |
8,067 |
21,748 |
6,865 |
|
09.XI |
114 |
114 |
5,77 |
91 |
4,736 |
1,753 |
8,190 |
21,835 |
7,003 |
1972 |
11.II |
146 |
146 |
5,59 |
89 |
4,984 |
1,721 |
8,492 |
24,349 |
12,196 |
|
07.III |
127 |
127 |
7,81 |
90 |
4,844 |
2,055 |
9,840 |
22,920 |
8,931 |
|
17.IV |
124 |
124 |
8,22 |
97 |
4,820 |
2,107 |
10,032 |
22,678 |
8,464 |
|
06.VII |
114 |
114 |
4,98 |
72 |
4,736 |
1,605 |
7,502 |
21,835 |
7,003 |
|
09.VIII |
121 |
121 |
6,91 |
79 |
4,796 |
1,933 |
9,155 |
22,432 |
8,010 |
1973 |
29.III |
134 |
134 |
1,08 |
100 |
4,898 |
0,077 |
0,373 |
23,466 |
10,071 |
|
27.VI |
118 |
118 |
6,70 |
75 |
4,771 |
1,902 |
8,958 |
22,180 |
7,570 |
|
05.X |
116 |
116 |
5,58 |
91 |
4,754 |
1,719 |
8,065 |
22,009 |
7,284 |
1974 |
30.III |
116 |
116 |
6,14 |
62 |
4,754 |
1,815 |
8,514 |
22,009 |
7,284 |
|
25.IV |
118 |
118 |
6,10 |
70 |
4,771 |
1,808 |
8,516 |
22,180 |
7,570 |
|
30.V |
116 |
116 |
6,19 |
60 |
4,754 |
1,823 |
8,552 |
22,009 |
7,284 |
|
07.VIII |
142 |
142 |
13,40 |
120 |
4,956 |
2,595 |
12,730 |
24,062 |
11,464 |
|
25.X |
208 |
208 |
47,60 |
280 |
5,338 |
3,863 |
20,486 |
28,125 |
26,656 |
1975 |
19.III |
124 |
124 |
10,50 |
80 |
4,820 |
2,351 |
11,198 |
22,678 |
8,464 |
|
09.IV |
126 |
126 |
11,90 |
81 |
4,836 |
2,477 |
11,836 |
22,840 |
8,774 |
|
17.IV |
159 |
159 |
24,30 |
120 |
5,069 |
3,190 |
16,029 |
25,239 |
14,741 |
|
21.IV |
153 |
153 |
25,10 |
120 |
5,030 |
3,223 |
16,062 |
24,836 |
13,535 |
|
13.V |
130 |
130 |
13,10 |
110 |
4,868 |
2,573 |
12,380 |
23,157 |
9,411 |
|
23.V |
120 |
120 |
9,18 |
80 |
4,787 |
2,217 |
10,481 |
22,348 |
7,862 |
|
27.VI |
139 |
139 |
15,20 |
81 |
4,934 |
2,721 |
13,288 |
23,842 |
10,930 |
|
08.VII |
117 |
117 |
8,01 |
75 |
4,762 |
2,081 |
9,780 |
22,095 |
7,426 |
|
05.VIII |
141 |
141 |
16,20 |
105 |
4,949 |
2,785 |
13,641 |
23,989 |
11,284 |
1976 |
16.III |
131 |
131 |
13,30 |
135 |
4,875 |
2,588 |
12,474 |
23,235 |
9,573 |
|
21.V |
116 |
116 |
9,81 |
85 |
4,754 |
2,283 |
10,712 |
22,009 |
7,284 |
|
14.VIII |
111 |
111 |
8,45 |
68 |
4,710 |
2,134 |
9,912 |
21,570 |
6,594 |
|
07.X |
112 |
112 |
7,55 |
70 |
4,718 |
2,022 |
9,408 |
21,659 |
6,729 |
|
21.X |
111 |
111 |
7,74 |
68 |
4,710 |
2,046 |
9,504 |
21,570 |
6,594 |
1977 |
11.III |
158 |
158 |
28,20 |
163 |
5,063 |
3,339 |
16,754 |
25,173 |
14,536 |
|
21.IV |
133 |
133 |
13,80 |
95 |
4,890 |
2,625 |
12,694 |
23,390 |
9,904 |
|
08.VII |
104 |
104 |
6,08 |
88 |
4,644 |
1,805 |
8,257 |
20,928 |
5,688 |
|
26.VIII |
116 |
116 |
8,60 |
80 |
4,754 |
2,152 |
10,095 |
22,009 |
7,284 |
1978 |
07.IV |
120 |
120 |
11,20 |
125 |
4,787 |
2,416 |
11,421 |
22,348 |
7,862 |
|
27.IV |
130 |
130 |
15,30 |
97 |
4,868 |
2,728 |
13,127 |
23,157 |
9,411 |
|
10.XI |
116 |
116 |
8,90 |
84 |
4,754 |
2,186 |
10,256 |
22,009 |
7,284 |
|
30.XI |
126 |
126 |
11,60 |
72 |
4,836 |
2,451 |
11,714 |
22,840 |
8,774 |
1979 |
06.III |
231 |
231 |
45,70 |
190 |
5,442 |
3,822 |
20,684 |
29,286 |
33,538 |
|
17.V |
111 |
111 |
10,80 |
105 |
4,710 |
2,380 |
11,052 |
21,570 |
6,594 |
|
28.VI |
94 |
94 |
5,77 |
72 |
4,543 |
1,753 |
7,827 |
19,944 |
4,516 |
|
09.VIII |
100 |
100 |
7,40 |
80 |
4,605 |
2,001 |
9,072 |
20,544 |
5,202 |
|
07.IX |
100 |
100 |
6,95 |
83 |
4,605 |
1,939 |
8,788 |
20,544 |
5,202 |
1980 |
14.II |
133 |
133 |
16,20 |
111 |
4,890 |
2,785 |
13,469 |
23,390 |
9,904 |
|
20.III |
112 |
112 |
8,53 |
60 |
4,718 |
2,144 |
9,976 |
21,659 |
6,729 |
|
09.V |
124 |
124 |
14,80 |
120 |
4,820 |
2,695 |
12,832 |
22,678 |
8,464 |
|
29.V |
102 |
102 |
7,40 |
85 |
4,625 |
2,001 |
9,114 |
20,738 |
5,442 |
|
12.VI |
125 |
125 |
13,10 |
100 |
4,828 |
2,573 |
12,273 |
22,759 |
8,618 |
|
29.VII |
244 |
244 |
73,00 |
245 |
5,497 |
4,290 |
23,460 |
29,900 |
37,799 |
|
30.VII |
228 |
228 |
60,10 |
240 |
5,429 |
4,096 |
22,111 |
29,140 |
32,593 |
|
03.IX |
114 |
114 |
12,00 |
95 |
4,736 |
2,485 |
11,612 |
21,835 |
7,003 |
|
28.X |
130 |
130 |
18,40 |
151 |
4,868 |
2,912 |
14,015 |
23,157 |
9,411 |
|
zmiana zera wodowskazu |
Tabela 2
|
|
|
|
|
4,83 |
2,27 |
11,07 |
23,39 |
23,33 |
W ostateczności:
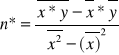
n*=2,12
![]()
a*=-7,96
![]()
ၡ*=0,000
Wzór naszej funkcji wygląda następująco:
Q = (H+152)^ 3,0237
lnQi =ln ၡ+n ln(Hi-ၢśr)
yi =A +n xi
yi = -15,9952+3,0237xi
Wykres krzywej przepływów:
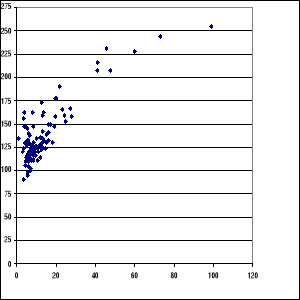
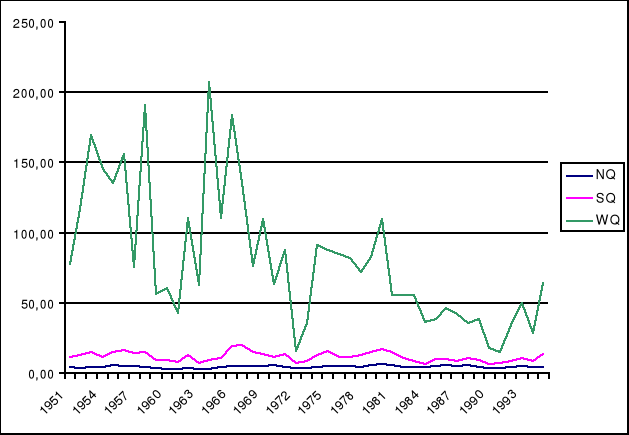
3. Przepływy charakterystyczne główne I i II rzędu oraz wykres zmienności przepływów głównych I rzędu
Tabela 2
Rok |
NQ |
SQ |
WQz |
WQl |
WQ |
1951 |
4,80 |
11,88 |
62,60 |
78,10 |
78,10 |
1952 |
4,02 |
13,21 |
117,00 |
49,90 |
117,00 |
1953 |
4,90 |
15,48 |
170,00 |
30,70 |
170,00 |
1954 |
4,30 |
12,08 |
146,00 |
47,60 |
146,00 |
1955 |
5,81 |
15,06 |
136,00 |
112,00 |
136,00 |
1956 |
5,20 |
16,38 |
156,00 |
24,30 |
156,00 |
1957 |
5,50 |
14,14 |
75,60 |
64,20 |
75,60 |
1958 |
4,16 |
15,01 |
191,00 |
12,80 |
191,00 |
1959 |
3,92 |
9,59 |
56,90 |
35,60 |
56,90 |
1960 |
3,11 |
9,59 |
60,50 |
61,20 |
61,20 |
1961 |
2,90 |
8,52 |
36,40 |
43,00 |
43,00 |
1962 |
3,82 |
12,89 |
111,00 |
101,00 |
111,00 |
1963 |
3,00 |
7,71 |
62,70 |
10,30 |
62,70 |
1964 |
3,10 |
10,01 |
208,00 |
13,10 |
208,00 |
1965 |
4,70 |
11,28 |
111,00 |
34,60 |
111,00 |
1966 |
5,08 |
19,53 |
184,00 |
88,30 |
184,00 |
1967 |
5,10 |
20,69 |
136,00 |
62,50 |
136,00 |
1968 |
4,92 |
14,91 |
76,40 |
21,90 |
76,40 |
1969 |
4,94 |
13,59 |
110,00 |
17,40 |
110,00 |
1970 |
6,02 |
12,25 |
63,50 |
49,80 |
63,50 |
1971 |
4,40 |
13,62 |
87,80 |
36,70 |
87,80 |
1972 |
3,85 |
7,36 |
14,10 |
15,50 |
15,50 |
1973 |
3,68 |
8,73 |
36,40 |
19,80 |
36,40 |
1974 |
4,50 |
12,79 |
29,00 |
91,70 |
91,70 |
1975 |
5,65 |
15,93 |
87,80 |
40,60 |
87,80 |
1976 |
5,40 |
12,42 |
85,20 |
16,00 |
85,20 |
1977 |
5,55 |
11,98 |
82,60 |
15,20 |
82,60 |
1978 |
4,89 |
12,52 |
72,40 |
49,00 |
72,40 |
1979 |
5,95 |
14,82 |
83,40 |
21,50 |
83,40 |
1980 |
6,84 |
17,49 |
50,30 |
110,00 |
110,00 |
1981 |
6,36 |
15,33 |
55,70 |
24,00 |
55,70 |
1982 |
4,54 |
11,57 |
56,00 |
17,60 |
56,00 |
1983 |
4,40 |
8,79 |
55,70 |
14,80 |
55,70 |
1984 |
4,46 |
7,01 |
11,70 |
36,90 |
36,90 |
1985 |
5,58 |
10,49 |
38,70 |
32,40 |
38,70 |
1986 |
5,77 |
10,64 |
46,90 |
10,90 |
46,90 |
1987 |
5,24 |
9,11 |
42,00 |
24,50 |
42,00 |
1988 |
6,40 |
11,03 |
35,90 |
25,60 |
35,90 |
1989 |
4,65 |
9,62 |
38,80 |
19,40 |
38,80 |
1990 |
4,10 |
6,93 |
18,00 |
9,44 |
18,00 |
1991 |
4,10 |
7,45 |
15,20 |
12,60 |
15,20 |
1992 |
4,63 |
9,30 |
25,10 |
34,50 |
34,50 |
1993 |
5,40 |
11,69 |
50,20 |
14,80 |
50,20 |
1994 |
4,63 |
8,95 |
29,00 |
24,30 |
29,00 |
1995 |
4,69 |
13,35 |
64,00 |
16,80 |
64,00 |
Przepływy główne II rzędu:
Tabela 3
NNQ |
SNQ |
WNQ |
2,90 |
4,78 |
6,84 |
NSQ |
SSQ |
WSQ |
6,93 |
12,06 |
20,69 |
NWQ |
SWQ |
WWQ |
15,20 |
81,42 |
208,00 |
4. Rozkład prawdopodobieństwa przepływów rocznych minimalnych
obliczenia równania krzywej teoretycznej rozkładu prawdopodobieństwa
wykres punktów rozkładu empirycznego i krzywej rozkładu teoretycznego na podziałce rozkładu normalnego
Tabela 4
L.P. |
NQ |
Qmin |
Q^2 |
q [%] |
1 |
4,80 |
2,90 |
8,41 |
2,17 |
2 |
4,02 |
3,00 |
9,00 |
4,35 |
3 |
4,90 |
3,10 |
9,61 |
6,52 |
4 |
4,30 |
3,11 |
9,67 |
8,70 |
5 |
5,81 |
3,68 |
13,54 |
10,87 |
6 |
5,20 |
3,82 |
14,59 |
13,04 |
7 |
5,50 |
3,85 |
14,82 |
15,22 |
8 |
4,16 |
3,92 |
15,37 |
17,39 |
9 |
3,92 |
4,02 |
16,16 |
19,57 |
10 |
3,11 |
4,10 |
16,81 |
21,74 |
11 |
2,90 |
4,10 |
16,81 |
23,91 |
12 |
3,82 |
4,16 |
17,31 |
26,09 |
13 |
3,00 |
4,30 |
18,49 |
28,26 |
14 |
3,10 |
4,40 |
19,36 |
30,43 |
15 |
4,70 |
4,40 |
19,36 |
32,61 |
16 |
5,08 |
4,46 |
19,89 |
34,78 |
17 |
5,10 |
4,50 |
20,25 |
36,96 |
18 |
4,92 |
4,54 |
20,61 |
39,13 |
19 |
4,94 |
4,63 |
21,44 |
41,30 |
20 |
6,02 |
4,63 |
21,44 |
43,48 |
21 |
4,40 |
4,65 |
21,62 |
45,65 |
22 |
3,85 |
4,69 |
22,00 |
47,83 |
23 |
3,68 |
4,70 |
22,09 |
50,00 |
24 |
4,50 |
4,80 |
23,04 |
52,17 |
25 |
5,65 |
4,89 |
23,91 |
54,35 |
26 |
5,40 |
4,90 |
24,01 |
56,52 |
27 |
5,55 |
4,92 |
24,21 |
58,70 |
28 |
4,89 |
4,94 |
24,40 |
60,87 |
29 |
5,95 |
5,08 |
25,81 |
63,04 |
30 |
6,84 |
5,10 |
26,01 |
65,22 |
31 |
6,36 |
5,20 |
27,04 |
67,39 |
32 |
4,54 |
5,24 |
27,46 |
69,57 |
33 |
4,40 |
5,40 |
29,16 |
71,74 |
34 |
4,46 |
5,40 |
29,16 |
73,91 |
35 |
5,58 |
5,50 |
30,25 |
76,09 |
36 |
5,77 |
5,55 |
30,80 |
78,26 |
37 |
5,24 |
5,58 |
31,14 |
80,43 |
38 |
6,40 |
5,65 |
31,92 |
82,61 |
39 |
4,65 |
5,77 |
33,29 |
84,78 |
40 |
4,10 |
5,81 |
33,76 |
86,96 |
41 |
4,10 |
5,95 |
35,40 |
89,13 |
42 |
4,63 |
6,02 |
36,24 |
91,30 |
43 |
5,40 |
6,36 |
40,45 |
93,48 |
44 |
4,63 |
6,40 |
40,96 |
95,65 |
45 |
4,69 |
6,84 |
46,79 |
97,83 |
|
|
|
|
|
|
średnia |
4,78 |
23,64 |
|
|
|
|
|
|
Rozkład prawdopodobieństwa określony jest za pomocą trzech parametrów: ၥ, ၑ i ၬ.
Najpierw obliczono następujące wartości:
![]()
ၳ= 0,89
Qmin,Sr= ქ Qmin /N
gdzie: N - liczba wyrazów ciągu (N = 45)
Współczynnik empiryczny:
![]()
estymator:
ၴ (ၬ, N)= (Qmin,Sr / Qmin,1)/ ၳ
ၴ (ၬ, N)= 2,11
parametr ၥ
![]()
gdzie: ၬ - zinterpolowana wartość parametru zależnego od ၴ (ၬ, N) dla N = 45 i ၴ = 2,11
ၬ = 0,28
Qmin,Sr = 4,78
Qmin,1 = 2,90
ၥ = 1,9
na końcu wylicza się parametry ၑ i ၇(1+ၬ):
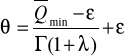
၇(1+ၬ) - funkcja odczytana z tabeli dla ၬ = 0,57 ( z interpolacji)
၇(1+ၬ) = 0,90072
Następnie wyznaczono minimalne przepływy roczne o określonym prawdopodobieństwie wystąpienia. Poszczególne wartości uzyskano ze wzoru:
![]()
Tabela 5
p [%] |
p [ - ] |
yp |
Qmin,p |
1 |
0,01 |
-4,60015 |
2,259 |
2 |
0,02 |
-3,90194 |
2,336 |
5 |
0,05 |
-2,97020 |
2,466 |
10 |
0,1 |
-2,25037 |
2,592 |
25 |
0,25 |
-1,24590 |
2,817 |
50 |
0,5 |
-0,36651 |
3,073 |
80 |
0,8 |
0,47588 |
3,385 |
90 |
0,9 |
0,83403 |
3,542 |
95 |
0,95 |
1,09719 |
3,668 |
99 |
0,99 |
1,52718 |
3,894 |
(Wykres punktów rozkładu empirycznego i krzywej rozkładu teoretycznego na podziałce rozkładu normalnego został dołączony na końcu razem z innymi załącznikami - wykres nr 3).
5. Rozkład prawdopodobieństwa przepływów maksymalnych rocznych
a)wydruk pliku danych dla programu QMAX oraz dla programu NJ, Rok, WQz, WQl
1951 78.100 62.600
1952 49.900 117.000
1953 30.700 170.000
1954 47.600 146.000
1955 112.000 136.000
1956 24.300 156.000
1957 64.200 75.600
1958 12.800 191.000
1959 35.600 56.900
1960 61.200 60.500
1961 43.000 36.400
1962 101.000 111.000
1963 10.300 62.700
1964 13.100 208.000
1965 34.600 111.000
1966 88.300 184.000
1967 62.500 136.000
1968 21.900 76.400
1969 17.400 110.000
1970 49.800 63.500
1971 36.700 87.800
1972 15.500 14.100
1973 19.800 36.400
1974 91.700 29.000
1975 40.600 87.800
1976 16.000 85.200
1977 15.200 82.600
1978 49.000 72.400
1979 21.500 83.400
1980 110.000 50.300
1981 24.000 55.700
1982 17.600 56.000
1983 14.800 55.700
1984 36.900 11.700
1985 32.400 38.700
1986 10.900 46.900
1987 24.500 42.000
1988 25.600 35.900
1989 19.400 38.800
1990 9.440 18.000
1991 12.600 15.200
1992 34.500 25.100
1993 14.800 50.200
1994 24.300 29.000
1995 16.800 64.000
b) pliki wynikowe z programów QMAX i NJ
Raport programu QMAXP
Wyniki obliczeń największych przepływów o określonym prawdopodobieństwie przewyższenia
Identyfikator danych: Rzeka: Tanew, wodowskaz: Harasiuki
PRZEPLYWY MAKSYMALNE ROCZNE ROZTOPOWE
PRZEPLYWY MAKSYMALNE ROCZNE ROZTOPOWE
Wartości charakterystyczne z próby o liczebności N=45 elementów
Najmniejszy element: 9.4
Największy element: 112.0
Średnia arytmetyczna: 37.6
Odchylenie standardowe: 27.6
Współczynnik zmienności: 0.734
Współczynnik skośności: 1.301
Najlepiej dopasowane funkcje poszczególnych typów rozkładów wg kryterium minimalnej odległości Kolmogorowa Dmax
Rozkład gamma: odległość Kolmogorowa Dmax = 6.114%
funkcja z dolnym ograniczeniem d= 9.4
z parametrami: alfa= 30.5, lambda=0.924
sprawdzian testu chi-kwadrat = 1.565
odrzucono 0
Rozkład Weibulla: odległość Kolmogorowa Dmax = 6.238%
funkcja z dolnym ograniczeniem d= 9.4
z parametrami: alfa= 27.8, beta=0.962
sprawdzian testu chi-kwadrat = 1.525
odrzucono 0 z 95 testowanych funkcji
Rozkład log-normalny: odległość Kolmogorowa Dmax = 6.683%
funkcja z dolnym ograniczeniem d= 6.4
z parametrami: mi=3.050, sigma=0.916
sprawdzian testu chi-kwadrat = 1.668
odrzucono 0 z 95 testowanych funkcji
Rozkład log-gamma: odległość Kolmogorowa Dmax = 7.338%
funkcja z dolnym ograniczeniem d= 4.0
z parametrami: alfa= 0.239, lambda= 8.388
sprawdzian testu chi-kwadrat = 2.031
odrzucono 0 z 94 testowanych funkcji
Wartość krytyczna testu chi-kwadrat = 9.488 na poziomie = 0.050
Wybór jednej najbardziej wiarygodnej funkcji rozkładu wg minimalnej wartości kryterium informacyjnego Akaike
Rozkład gamma: 394.41246 < wartość minimalna
Rozkład Weibulla: 394.49118
Rozkład log-normalny: 398.34787
Rozkład log-gamma: 399.83843
ROZKLAD PRAWDOPODOBIENSTWA PRZEPLYWOW MAKSYMALNYCH ROCZNYCH ROZTOPOWYCH
Najbardziej wiarygodna jest funkcja rozkładu gamma
z dolnym ograniczeniem d= 9.4
oraz estymatorami MNW parametrów: alfa= 30.5, lambda=0.924
PRZEPLYWY MAKSYMALNE ROCZNE DESZCZOWE
Wartości charakterystyczne z próby o liczebności N=45 elementów
Najmniejszy element: 11.7
Największy element: 208.0
Średnia arytmetyczna: 77.4
Odchylenie standardowe: 49.6
Współczynnik zmienności: 0.641
Współczynnik skośności: 0.954
Najlepiej dopasowane funkcje poszczególnych typów rozkładów wg kryterium minimalnej odległości Kolmogorowa Dmax
Rozkład gamma: odległość Kolmogorowa Dmax = 6.305%
funkcja z dolnym ograniczeniem d= 7.9
z parametrami: alfa= 39.6, lambda=1.753
sprawdzian testu chi-kwadrat = 0.963
odrzucono 0 z 117 testowanych funkcji
Rozkład Weibulla: odległość Kolmogorowa Dmax = 6.892%
funkcja z dolnym ograniczeniem d= 10.6
z parametrami: alfa= 72.2, beta=1.309
sprawdzian testu chi-kwadrat = 1.239
odrzucono 0 z 117 testowanych funkcji
Rozkład log-normalny: odległość Kolmogorowa Dmax = 8.204%
funkcja z dolnym ograniczeniem d= 0.0
z parametrami: mi=4.130, sigma=0.698
sprawdzian testu chi-kwadrat = 0.646
odrzucono 1 z 117 testowanych funkcji
Rozkład log-gamma: odległość Kolmogorowa Dmax = 9.765%
funkcja z dolnym ograniczeniem d= 0.1
z parametrami: alfa= 0.079, lambda= 81.329
sprawdzian testu chi-kwadrat = 0.917
odrzucono 2 z 116 testowanych funkcji
Wartość krytyczna testu chi-kwadrat = 9.488 na poziomie = 0.050
Wybór jednej najbardziej wiarygodnej funkcji rozkładu wg minimalnej wartości kryterium informacyjnego Akaike
Rozkład gamma: 468.49424
Rozkład Weibulla: 467.61174 <wartość minimalna
Rozkład log-normalny: 470.96198
Rozkład log-gamma: 472.58061
ROZKLAD PRAWDOPODOBIENSTWA PRZEPLYWOW MAKSYMALNYCH ROCZNYCH DESZCZOWYCH
Najbardziej wiarygodna jest funkcja rozkładu Weibulla
z dolnym ograniczeniem d= 10.6
oraz estymatorami MNW parametrów: alfa= 72.2, beta=1.309
NAJWIEKSZE PRZEPLYWY ROCZNE O OKRESLONYM PRAWDOPODOBIENSTWIE PRZEWYZSZENIA
jako kwantyle funkcji prawdopodobieństwa alternatywy
Prawdop. Przepływ Przedział Błąd Granice obszaru niepewności altern. maksymalny ufności kwantyla kwantyla
p[%] Qmax,p P84% sigma[%] dolna górna
99.90 12.5 13.2 5.70 7.2 LG-LN 13.2 LG-LG
99.50 15.0 16.2 8.19 14.8 GA-GA 16.5 LG-LG
99.00 16.9 18.4 9.13 16.9 GA-WE 18.5 LG-LG
98.50 18.3 20.1 9.59 18.3 GA-WE 20.0 LG-LG
98.00 19.5 21.5 9.87 19.5 GA-WE 21.1 LG-LG
95.00 25.0 27.6 10.41 24.9 LG-WE 26.3 WE-LN
90.00 31.6 34.9 10.40 31.1 LG-WE 32.5 GA-LN
80.00 42.4 46.6 9.99 40.6 LG-LG 42.6 GA-GA
70.00 52.2 57.2 9.57 49.0 LG-LG 52.2 GA-GA
60.00 62.2 67.9 9.20 58.0 LG-LG 62.2 GA-WE
50.00 72.9 79.4 8.93 68.3 LG-LG 72.9 GA-WE
40.00 85.1 92.5 8.78 80.7 WE-LG 85.4 LG-WE
30.00 99.8 108.6 8.84 96.1 WE-LG 101.1 LG-WE
20.00 119.3 130.4 9.27 117.7 GA-LN 122.1 LG-WE
10.00 150.6 166.4 10.50 150.6 GA-WE 169.1 LG-LG
5.00 180.1 201.6 11.93 180.1 GA-WE 224.1 LG-LG
2.00 217.1 247.0 13.78 217.1 GA-WE 311.9 LG-LG
1.00 243.9 280.7 15.06 243.9 GA-WE 392.0 LG-LG
0.50 269.9 313.7 16.23 269.9 GA-WE 486.1 LG-LG
0.20 302.2 355.7 17.71 302.2 GA-WE 587.7 LG-LG
0.10 326.7 388.0 18.78 326.7 GA-WE 707.9 LG-LG
0.05 350.6 420.5 19.91 350.6 GA-WE 845.9 LG-LG
0.02 381.5? 462.2 21.13 381.5 GA-WE 1059.6 LG-LG
0.01 404.4? 492.8 21.86 404.4 GA-WE 1248.1 LG-LG
UWAGA: znak zapytania przy wartości kwanyla oznacza, ze błąd kwantyla
jest większy od 20% (liczebność próby losowej jest zbyt mała).
Zastosowane skróty oznaczeń typów rozkładów: GA - rozkład gamma,
WE - rozkład Weibulla,
LN - rozkład log-normalny,
LG - rozkład log-gamma,
Raport programu NJ
Wyniki obliczeń analizy danych pomiarowych
Identyfikator danych: Rzeka: Tanew wodowskaz: Harasiuki
Przepływy maksymalne roczne roztopowe
Weryfikacja elementów odstających - Test Grubbsa i Becka
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000
w badanym ciągu nie zostały wykryte elementy odstające.
Weryfikacja niezależności - Test serii
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000 nie ma podstaw do odrzucenia hipotezy zerowej Ho, co świadczy o losowym wyborze elementów do badanego ciągu i oznacza, ze badana zmienna losowa jest niezależna.
Weryfikacja stacjonarności - Test sumy rang Kruskala-Wallisa
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000 należy odrzucić hipotezę zerowa Ho, co oznacza, ze w ciągu wykryto skok wartości średniej, tj. ciąg pomiarowy jest niestacjonarny.
Weryfikacja stacjonarności
Test współczynnika korelacji rangowej Spearmana na trend wartości średniej
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000 należy odrzucić hipotezę zerową Ho, co oznacza, ze badany ciąg pomiarowy posiada ujemny trend wartości średniej i jest niestacjonarny.
Weryfikacja stacjonarności
Test współczynnika korelacji rangowej Spearmana na trend wariancji
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000
nie ma podstaw do odrzucenia hipotezy zerowej Ho, co oznacza, ze badany
ciąg pomiarowy nie posiada trendu wariancji i jest stacjonarny.
Przepływy maksymalne roczne deszczowe
Weryfikacja elementów odstających - Test Grubbsa i Becka
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000
w badanym ciągu nie zostały wykryte elementy odstające.
Weryfikacja niezależności - Test serii
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000
należy odrzucić hipotezę zerowa Ho, co oznacza, ze badana zmienna losowa
jest zmienna zależną.
Weryfikacja stacjonarności - Test sumy rang Kruskala-Wallisa
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000
należy odrzucić hipotezę zerowa Ho, co oznacza, ze w ciągu wykryto skok
wartości średniej, tj. ciąg pomiarowy jest niestacjonarny.
Weryfikacja stacjonarności
Test współczynnika korelacji rangowej Spearmana na trend wartości średniej
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000
należy odrzucić hipotezę zerowa Ho, co oznacza, ze badany ciąg pomiarowy
posiada ujemny trend wartości średniej i jest niestacjonarny.
Weryfikacja stacjonarności
Test współczynnika korelacji rangowej Spearmana na trend wariancji
Wynik testowania: Na przyjętym poziomie istotności ŕ = 0.1000
nie ma podstaw do odrzucenia hipotezy zerowej Ho, co oznacza, ze badany
ciag pomiarowy nie posiada trendu wariancji i jest stacjonarny.
6. Przepływy o określonym czasie trwania
b) Histogram częstości gęstości przepływów dobowych - wykr. Nr 5
c) Wartość wyznaczonego przepływu modalnego - wykr. Nr 6
d) Wykres krzywych sum czasów trwania przepływów - wykr. Nr 7
(wykresy są w załącznikach).
Tabela z obliczeniami
Wyznaczamy iloraz an (współczynnik amplitudy) :
Z danych z lat 1991 - 1995 odczytujemy Qmax i Qmin:
Qmax = 64,000 [m3/s]
Qmin = 4,100 [m3/s]
![]()
-współczynnik amplitudy
an =15,6098
Do wyznaczenia liczby przedziałów r przyjęliśmy podział logarytmiczny:
0,5 * ln an < r < 10,5 * ln an
15,11 < r < 28,85 => r = 22
Dolne granice każdego z przedziałów wyznaczyliśmy ze wzoru:
![]()
Średnią częstość przepływu obliczamy ze wzoru:
wśr = ![]()
(w1+w2+w3+w4+w5)
Czas trwania przepływu wraz z wartościami niższymi obliczyliśmy ze wzoru:
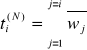
Natomiast czas trwania przepływu wraz z wartościami wyższymi obliczyliśmy ze wzoru:
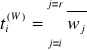
Wszystkie obliczone wartości umieściliśmy w tabeli poniżej.
Lp. |
dolne granice |
górne granice |
1991 |
1992 |
1993 |
1994 |
1995 |
średnia częstość |
ti1 |
ti2 |
gęstość |
szerokośćprzedziału |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4,100 |
4,645 |
22 |
2 |
0 |
5 |
0 |
5,80 |
5,80 |
365,20 |
10,633 |
0,545 |
2 |
4,645 |
5,263 |
35 |
61 |
0 |
72 |
46 |
42,80 |
48,60 |
359,40 |
69,252 |
0,618 |
3 |
5,263 |
5,964 |
69 |
23 |
59 |
42 |
19 |
42,40 |
91,00 |
316,60 |
60,549 |
0,700 |
4 |
5,964 |
6,757 |
51 |
43 |
67 |
29 |
38 |
45,60 |
136,60 |
274,20 |
57,473 |
0,793 |
5 |
6,757 |
7,656 |
43 |
59 |
43 |
36 |
12 |
38,60 |
175,20 |
228,60 |
42,938 |
0,899 |
6 |
7,656 |
8,675 |
47 |
47 |
31 |
62 |
25 |
42,40 |
217,60 |
190,00 |
41,627 |
1,019 |
7 |
8,675 |
9,829 |
43 |
20 |
26 |
25 |
11 |
25,00 |
242,60 |
147,60 |
21,662 |
1,154 |
8 |
9,829 |
11,136 |
26 |
21 |
21 |
20 |
31 |
23,80 |
266,40 |
122,60 |
18,201 |
1,308 |
9 |
11,136 |
12,618 |
15 |
20 |
8 |
9 |
30 |
16,40 |
282,80 |
98,80 |
11,069 |
1,482 |
10 |
12,618 |
14,297 |
7 |
16 |
8 |
17 |
20 |
13,60 |
296,40 |
82,40 |
8,101 |
1,679 |
11 |
14,297 |
16,199 |
7 |
5 |
21 |
11 |
27 |
14,20 |
310,60 |
68,80 |
7,466 |
1,902 |
12 |
16,199 |
18,354 |
0 |
25 |
19 |
13 |
23 |
16,00 |
326,60 |
54,60 |
7,424 |
2,155 |
13 |
18,354 |
20,796 |
0 |
16 |
19 |
8 |
18 |
12,20 |
338,80 |
38,60 |
4,996 |
2,442 |
14 |
20,796 |
23,562 |
0 |
1 |
7 |
4 |
21 |
6,60 |
345,40 |
26,40 |
2,386 |
2,767 |
15 |
23,562 |
26,697 |
0 |
5 |
11 |
8 |
16 |
8,00 |
353,40 |
19,80 |
2,552 |
3,135 |
16 |
26,697 |
30,249 |
0 |
0 |
10 |
4 |
11 |
5,00 |
358,40 |
11,80 |
1,408 |
3,552 |
17 |
30,249 |
34,273 |
0 |
0 |
8 |
0 |
9 |
3,40 |
361,80 |
6,80 |
0,845 |
4,024 |
18 |
34,273 |
38,833 |
0 |
2 |
2 |
0 |
3 |
1,40 |
363,20 |
3,40 |
0,307 |
4,560 |
19 |
38,833 |
43,999 |
0 |
0 |
3 |
0 |
1 |
0,80 |
364,00 |
2,00 |
0,155 |
5,166 |
20 |
43,999 |
49,853 |
0 |
0 |
1 |
0 |
3 |
0,80 |
364,80 |
1,20 |
0,137 |
5,854 |
21 |
49,853 |
56,485 |
0 |
0 |
1 |
0 |
0 |
0,20 |
365,00 |
0,40 |
0,030 |
6,632 |
22 |
56,485 |
64,000 |
0 |
0 |
0 |
0 |
1 |
0,20 |
365,20 |
0,20 |
0,027 |
7,515 |
suma |
|
365 |
366 |
365 |
365 |
365 |
|
|
|
|
|
|
Tabela 6
Wartość przeciętnego przepływu Qmod odczytaliśmy z wykresu na papierze milimetrowym.
Qmod = m3/s
7. Obliczenia wartości wybranych przepływów konwencjonalnych
Qdoz - przepływ dozwolony, max przepływ roczny o prawdopodobieństwie przewyższenia 50%, największa wartość przepływu nie powodująca strat na korycie rzecznym
Qdop - przepływ dopuszczalny, max przepływ roczny o prawdopodobieństwie przewyższenia 40%
Qnh - przepływ nienaruszalny, minimalna wartość natężenia przepływu, stosuje się kryterium hydrologiczne - uniwersalne
Qb,t - przepływ brzegowo twórczy, powoduje największe zmiany koryta rzecznego, wartość tą odczytuje się z wykresu
Obliczono przepływ nienaruszalny ![]()
uwzględniając kryterium hydrobiologiczne metodą uproszczoną wg Kostrzewy, tj. metodą parametryczną. W tym celu określono typ hydrologiczny rzeki (THR) z tabeli 1 dla średniego spływu jednostkowego ![]()
obliczanego z następującego wzoru:
![]()
gdzie:
![]()
- średni spływ jednostkowy w, [1/s/km2]
![]()
- przepływ główny II rzędu średni z przepływów średnich, ![]()
- powierzchnia zlewni: 2034 km2
q = 5,929 [1/s/km2]
Tabela 7
Typ hydrologiczny rzeki (THR) |
Średni spływ powierzchniowy
|
Podgórski i przejściowy (Pg i Pr) |
|
Przepływ nienaruszalny hydrobiologiczny ![]()
należy obliczyć z następującego wzoru:
![]()
gdzie
![]()
- bezwymiarowy parametr zależny od typu hydrologicznego rzeki THR i powierzchni zlewni ![]()
, tj. k = f(THR, A),
![]()
- przepływ główny II rzędu średni z przepływów niskich w ![]()
,
Przy czym powinna być spełniona nierówność ![]()
. Jeżeli ![]()
to należy przyjąć ![]()
.
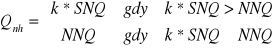
A - obszar zlewni
Th - typ hydrologiczny rzeki
k = 0,52
WWQ = 208,00 [m3/s]
SNQ = 4,78 [m3/s]
NNQ = 2,90 [m3/s]
k * SNQ = 0,5 *4,78 [m3/s] = 2,797 [m3/s] < NNQ więc Qn,h = 2,90 [m3/s]
Qn,h = 2,90 [m3/s]
Qdoz = Qmax, 50% = 72,9 [m3/s]
Qdop = Qmax, 40% = 85,1 [m3/s]
(dane uzyskane z programu QMAX).
![]()
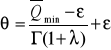
![]()
Wyszukiwarka
Podobne podstrony:
PROJEKCIK ekonomika wersja3 ostateczna, Ochrona Środowiska, semestr VI, Ekonomika i finanse ochrony
projekt transport wersja ostateczna
projekt zarzadzanie wersja ostateczna (dupa 95d4d55fb2 s conflicted copy 2012 03 07)
projekt zarzadzanie wersja ostateczna
projekt zarzadzanie wersja ostateczna (deleted 4f564ccc 1a600 f8167346)
Ćwiczenie projektowe nr 1, Studia Budownictwo polsl, I semestr, Hydrologia i hydraulika, projekt
projekt3, NAUKA, Politechnika Bialostocka - budownictwo, Semestr III od Karola, Hydraulika i Hydrolo
Hydrologia projekt 1, Hydrologia Rafał
projekt 1 zabezpieczenie mieszkania OSTATECZNA WERSJA
Prawo miejscowe-referat wersja ostateczna, I SEMESTR, streszczenia na egzamin
hydrologia projekty hydrologiaI
badania almatur wersja ostateczna, wshiu poznan, semestr IV, badania rynku
zagadnienia z hydrologi odpowiedzi, Materiały, Inżynieria Środowiska, Semestr 2, Hydrologia i meteor
hydrologia projekty HydrologiaIIIwykrtesy
rzeka - projekt, Hydrologia 1
DK 9 1 2 wersja ostateczna, Zarządzanie projektami(20)
Projekt wersja ostateczna
więcej podobnych podstron