Mariusz Ruchniak

ΙΙΙ - rok Wydział Mechaniczny

Automatyka okrętowa - praca kontrolna

Część Ι - zestaw MECH/VΙΙΙ

1. Jakie własności cechują ciągłe regulatory P , PD ?

2. Przeanalizować własności elementu oscylacyjnego w zależności od wartości współczynnika tłumienia ξ .

3. Opisać metodę doboru nastaw wg Hanssena i Offereinsa oraz porównać tę metodę z regułą doboru nastaw wg Zieglera - Nicholsa .

4. Przedstawić schemat blokowy , zasadę działania , parametry charakteryzujące przebieg wielkości regulowanej oraz konkretną realizację techniczną i występujące w niej elementy dwustawnego układu regulacji ciśnienia .

5. Analogowe i cyfrowe sposoby pomiaru prędkości obrotowej .

Ad 1) Jakie własności cechują ciągłe regulatory P , PD ?

Regulator proporcjonalny posiadający algorytm P , jest regulatorem konwencjonalnym , mającym ciągły sygnał wyjściowy . Jego sygnał wyjściowy jest proporcjonalny do sygnału wejściowego . Pracuje on zgodnie z prawem regulacji , które można przedstawić u(t)=k_pε(t) . Transmitancja regulatora proporcjonalnego wynosi G_p(s)=k_p . Charakterystyka skokowa regulatora proporcjonalnego wygląda następująco :

u(t)

k_p t

Sygnał wyjściowy u(t) regulatora proporcjonalnego

ε(t)

1(t)

t Sygnał wejściowy ε(t)

Jedną z cech regulatorów proporcjonalnych jest to , że przy współpracy regulatora z obiektem inercyjnym nie jest on w stanie sprowadzić błędu ustalonego do zera . Wadą regulatorów typu P jest konieczność kompromisowego dobierania wartości współczynnika wzmocnienia . Mały współczynnik wzmocnienia powoduje długi czas regulacji oraz daje duży błąd w stanie ustalonym , natomiast duży współczynnik wzmocnienia powoduje powstanie przebiegów silnie oscylacyjnych .

Wymagania dokładności statycznej (małego błędu) oraz stabilność układu automatycznej regulacji są wzajemnie sprzeczne . Nastawa regulatora proporcjonalnego wynika więc bezpośrednio z kompromisu pomiędzy wymaganiami stabilności i dokładności w stanie ustalonym .

Regulatory proporcjonalne są stosowane do regulacji następujących obiektów oraz układów :

• obiekty o niedużych wartościach stałych czasowych i małych opóźnieniach oraz stałych zakłóceniach działających na układ

• w układach gdzie dopuszczalny jest błąd w stanie ustalonym

• w układach regulacji kaskadowej jako regulatory pomocnicze

• elementy regulatorów o złożonych charakterystykach

Podstawową zaletą regulatorów proporcjonalnych jest ich duża szybkość działania .

Wielkością jaką charakteryzują się regulatory typu P jest współczynnik wzmocnienia k_p oraz zakres proporcjonalności wyrażony zależnością :

x_p=
100%

Zakres proporcjonalności określa , przy jakim zakresie zmian sygnału uchybu (który jest sygnałem wejściowym regulatora) jest zachowana proporcjonalność między wartością sygnału uchybu , a wartością sygnału wyjściowego regulatora proporcjonalnego .

Regulator proporcjonalno - różniczkujący ( PD ) .

Regulator o algorytmie PD jest konwencjonalnym regulatorem posiadającym ciągły sygnał wyjściowy . W idealnym regulatorze PD sygnał wyjściowy u(t) jest proporcjonalny do sumy sygnału wejściowego ε(t) oraz do pochodnej tego sygnału :

u(t)=k_p
ε(t)+T_d

k_p - współczynnik wzmocnienia

T_d - czas różniczkowania regulatora

Charakterystyka skokowa regulatora PD :

u(t)

∞

k_p

t

ε(t)

1(t)

t

Odpowiedź skokowa u(t) idealnego regulatora PD .

u(t)

2k_pA_tT_d

k_pA_tT_d

0 t

T_d

ε(t) ε(t)=A₁t

0 t

Odpowiedź regulatora PD na sygnał liniowo narastający .

T_d - czas różniczkowania - jest to czas który określa właściwości części różniczkującej regulatora i jest liczbowo równy stałej czasowej różniczkowania . Różniczkowanie powoduje wprowadzenie do sygnału wyjściowego regulatora składnika proporcjonalnego do szybkości zmian uchybu , a więc w przypadku stałej szybkości zmian uchybu sygnał ulega jak gdyby wyprzedzeniu w stosunku do składnika proporcjonalnego w sygnale regulatora , ponieważ w składniku proporcjonalnym uwzględnia się tylko aktualną wartość uchybu .

Podstawową zaletą regulatora PD jest poprawa właściwości dynamicznych regulatora , wskutek działania elementu różniczkującego . Dzięki temu działaniu regulator skutecznie reaguje na pojawienie się zakłóceń , co eliminuje powstawanie przebiegów oscylacyjnych . Zapewniona jest równocześnie dobra regulacja w szerokim paśmie częstotliwości . Regulator PD nie jest jednak w stanie sprowadzić do zera uchybu regulacji ale zmniejsza przeregulowanie i skraca czas regulacji . Stosowane są tego typu regulatory do regulacji obiektów o średnich wartościach stałych czasowych poddanych działaniu małych i szybkich zakłóceń .

Ad 2 ) Przeanalizować własności elementu oscylacyjnego w zależności od wartości współczynnika tłumienia ξ .

Ogólna postać równania różniczkowego , które ułatwia interpretację przebiegów przejściowych elementu oscylacyjnego jest następująca :

przy czym ξ < 1 . Transmitancja wówczas ma postać :

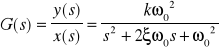
k - współczynnik proporcjonalności

ω =
- pulsacja oscylacji własnych elementu , ξ =

- zredukowany (względny) współczynnik tłumienia

T₁ , T₂ - stałe czasowe elementu

Charakterystyka statyczna elementu oscylacyjnego :

y

x

Współrzędne odchyłek .

y₀

C

x₀

Współrzędne wartości absolutnych .

Odpowiedź na wymuszenie skokowe będzie mieć charakter oscylacyjny , jeżeli spełniony jest warunek :

T₂² < 4T₁²

lub co jest jednoznaczne :

ξ < 1

Odpowiedź elementu oscylacyjnego na wymuszenie skokowe 1(t)x_st wygląda następująco :

y

kx_st

T T

t

Składowa ustalona przebiegu wynosi kx_st , a składowa przejściowa jest gasnącą sinusoidą , której okres jest stały i wynosi :

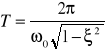
W przypadku szczególnym , kiedy ξ = 0 ( tzn. T₂ = 0 ) , występują drgania zachowawcze ( nie tłumione ) o pulsacji ω₀ . Jeżeli T₂² > 4T₁² , czyli ξ > 1 , to przebieg y(t) traci charakter oscylacyjny . Składowa przejściowa przebiegu jest wówczas sumą dwóch krzywych wykładniczych , zatem y(t) osiąga aperiodycznie wartość ustaloną kx_st .

Jeżeli T₂² = 4T₁² , czyli ξ = 1 , występuje tzw. tłumienie krytyczne . Jest to również przebieg aperiodyczny , podobnie jak dla przypadku T₂² > 4T₁² .

W przypadku kiedy nie występują przebiegi oscylacyjne , tzn. dla
, elementy traktuje się jako inercyjne drugiego rzędu .

k

t

Odpowiedzi elementu oscylacyjnego w zależności

od współczynnika tłumienia ξ .

Ad 3 ) Opisać metodę doboru nastaw wg Hanssena i Offereinsa oraz porównać tę metodę z regułą doboru nastaw wg Zieglera - Nicholsa .

Metody ścisłej analizy teoretycznej , które umożliwiają wyznaczenie dowolnych właściwości układu automatycznej regulacji , nie nadają się do wyznaczania wartości nastaw regulatorów uniwersalnych . Podstawowym problemem dotyczącym doboru parametrów regulatorów jest taki dobór wartości nastaw , przy których uzyskujemy zadowalające działanie układu . Najbardziej rozpowszechnionymi metodami są metoda Zieglera - Nicholsa oraz metoda Hanssena i Offereinsa .

Stosując metodę Zieglera - Nicholsa , regulator połączony z obiektem ustawia się na działanie proporcjonalne (P) . Działanie całkujące i różniczkujące powinny być wyłączone przez nastawienie T_i = ∞ oraz T_d = 0 . Następnie zwiększając stopniowo wzmocnienie k_p regulatora doprowadza się układ do granicy stabilności , czyli aż do wystąpienia oscylacji niegasnących w układzie . Notując wartość współczynnika wzmocnienia regulatora k_kr , przy którym powstają oscylacje , oraz okres t_osc tych oscylacji , przyjmuje się odpowiednio :

• dla regulatora typu P - k_p = 0,5 k_kr

• dla regulatora typu PI - k_p = 0,45 k_kr , T_i = 0,85 t_osc

• dla regulatora typu PID - k_p = 0,6 k_kr , T_i = 0,5 t_osc , T_d = 0,12 t_osc

Metoda Zieglera - Nicholsa ma ścisły związek z korekcją charakterystyk dynamicznych . Uzależnia ona zalecaną wartość wzmocnienia regulatora od wzmocnienia krytycznego układu bez korygowanych charakterystyk dynamicznych oraz punkty załamań charakterystyki dynamicznej regulatora od wartości częstotliwości krytycznej układu bez korekcji . Zaletą tej metody są obliczone wartości nastaw które gwarantują stabilność układu regulacji .

Metoda doboru nastaw regulatorów według Hannsena i Offereinsa ściśle opiera się na metodzie Zieglera - Nicholsa . Zasadniczą różnicą jest pominięcie w metodzie Hannsena i Offereinsa pomiaru okresu oscylacji .

Regulator typu PI nastawia się w następujący sposób :

• nastawić czas całkowania T_i = ∞ ( max )

• doprowadzić układ do granicy stabilności i określić k_pkryt , zwiększając współczynnik wzmocnienia regulatora k_p

• przyjąć nastawę k_p = 0,45 k_pkryt

• zmniejszać czas całkowania T_i do wartości T_ikryt , przy której występuje niestabilność układu

• nastawić T_i = 3 T_ikryt

W przypadku regulatora typu PID należy :

• wykonać wszystkie czynności jak dla regulatora PI

• zwiększać czas różniczkowania T_d do wartości T_dmax , przy której występuje maksymalne tłumienie

• nastawić
  

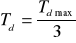
• ustawić czas całkowania T_i = 4,5 T_d

• zmniejszyć k_p aż do uzyskania pożądanego tłumienia

Ad 4 ) Przedstawić schemat blokowy , zasadę działania , parametry charakteryzujące przebieg wielkości regulowanej oraz konkretną realizację techniczną i występujące w niej elementy dwustawnego układu regulacji ciśnienia .

Regulacja dwupołożeniowa jest to taka regulacja , której sygnał błędu przerabiany jest na sygnał sterujący obiektem który przyjmuje tylko dwie wartości .

Przykładem układu regulacji ciśnienia z wykorzystaniem regulacji dwupołożeniowej jest układ regulacji ciśnienia pary w kotle . Charakterystyczną cechą takiego sposobu regulacji jest wykonywanie przez wielkość regulowaną , w tym przypadku ciśnienie pary , ciągłych oscylacji wokół wartości zadanej (y₀) . Wykonywane oscylacje nie są objawem utraty stabilności przez układ , a amplituda tych oscylacji nie zależy od wartości zadanej .

Przebieg wielkości regulowanej y(t) w układzie regulacji dwupołożeniowej :

y

y_u

y₂

y₀

y₁

t

y₀ - wartość zadana

y₁ - minimalna wartość ciśnienia pary - następuje załączenie palnika

y₂ - maksymalna wartość ciśnienia pary - następuje wyłączenie palnika

Przebieg y(t) składa się z kolejnych odcinków odpowiedzi elementu inercyjnego na wymuszenie skokowe , którymi są załączenia i wyłączenia palnika .

W układzie regulacji ciśnienia pary w kotle elementem dwustawnej regulacji jest palnik załączający się okresowo , to znaczy w przypadku nadmiernego spadku ciśnienia pary . Rolę regulatora spełnia w tym układzie przekaźnik dwupołożeniowy , który powoduje załączenie i wyłączenie palnika przy odpowiednich ciśnieniach pary .

x x

x_max x_max

1 2 1 2

x_min y x_min y

y₀ y₀

Charakterystyki statyczne regulatorów dwupołożeniowych : a) idealnego b) z histerezą ; 1 - zestyk zamknięty , 2 - zestyk otwarty

Przebieg sygnału wyjściowego regulatora dwupołożeniowego :

x

T

t_a t_b

x_max

x_min t

Schemat blokowy przedstawiający układ regulujący ciśnienie pary w kotle :

A

R

W przedstawionym wyżej układzie znajduje się element który dokonuje pomiaru wielkości regulowanej ( ciśnienie pary w kotle ) . Sygnał wysyłany z tego elementu trafia do przetwornika , gdzie zostaje zamieniony na sygnał znormalizowany .

Przykładem przetwornika może być urządzenie które składa się z czujnika w postaci rurki Bourdona i przetwornika pośredniego , działającego na zasadzie kompensacji sił. Sygnałem wyjściowym jest siła proporcjonalna do mierzonego ciśnienia . Siła ta przetwarzana jest w przetworniku pośrednim na sygnał pneumatyczny w postaci ciśnienia wyjściowego z przetwornika . Następnie sygnał ten dochodzi do węzła porównującego . Zadaniem tego elementu jest zbadanie różnicy pomiędzy wartością zadaną , a wartością rzeczywistą . W przypadku niższego ciśnienia pary w kotle od ciśnienia zadanego , regulator powoduje uruchomienie palnika . Istnieje również możliwość wybrania rodzaju pracy poprzez specjalny przełącznik wyboru rodzaju pracy ( ręczna lub automatyczna ) .

Ad 5 ) Analogowe i cyfrowe sposoby pomiaru prędkości obrotowej .

Pomiaru prędkości kątowej możemy dokonać za pomącą czujników , które w zależności od rozwiązania ich konstrukcji mogą być tachometrami analogowymi lub cyfrowymi .

1. Analogowe czujniki prędkości obrotowej .

1. Tachometr pneumatyczny .

W tachometrze tym sygnałem wyjściowym jest ciśnienie powietrza p_m . Tachometr składa się z cylindra 1 obracającego się dookoła osi 2 . W cylindrze umieszczony jest tłoczek 3 pozostający pod działaniem siły odśrodkowej równoważnej siłą od ciśnienia przepływającego przez cylinder powietrza . Ciśnienie to zależy od stopnia przymknięcia otworu 4 przez tłoczek i jest miarą prędkości kątowej , z jaką obraca się cylinder .

p_m = C ω²

C - stała przyrządu

b) Tachometr hydrauliczny .

Na podobnej zasadzie jak tachometr pneumatyczny działa również tachometr hydrauliczny . Wielkością wejściową jest prędkość kątowa ω wałka 1 , a wyjściową ciśnienie oleju p_m . Wałek 1 napędza zębatą pompę olejową 2 i obraca element 3 . Wydajność pompy jest proporcjonalna do prędkości ω , a ciśnienie p_m zależy od otwarcia zaworu 4 . Otwarcie to uwarunkowane jest zrównaniem się sił działających na tłoczek 5 : siły odśrodkowej i siły od ciśnienia p_m .

2. Cyfrowe sposoby pomiaru prędkości obrotowej .

W cyfrowy układ pomiaru prędkości obrotowej wyposażony jest cyfrowy regulator prędkości obrotowej stosowany na spalinowych silnikach okrętowych : regulator EGS 2000 . System pomiaru prędkości obrotowej Tacho jest wewnętrznym systemem tego regulatora i pozwala na pomiar prędkości kątowej wału silnika . Umieszczony jest on bezpośrednio przy kole zamachowym silnika . System zawiera w sobie między innymi dwa czujniki indukcyjne zamocowane na wsporniku tak jak pokazuje to rysunek . Czujniki te reagują na przesuwające się zęby obracającego się koła zamachowego . Pozostała część systemu znajduje się w jednostce centralnej regulatora i zawiera układ elektroniczny którego zadaniem jest szybkie przetwarzanie sygnałów wysyłanych przez czujniki . Umieszczenie dwóch czujników przy kole zamachowym spowodowane jest stworzeniem pewnej rezerwy w postaci jednego z tych czujników . Pomiaru dokonuje tylko jeden z zamontowanych czujników . Rejestruje on przesunięcie każdego zęba koła zamachowego i wysyła impulsy do wejściowych obwodów tachometrycznych w jednostce centralnej . Częstotliwość impulsów jest przetwarzana przez system EGS 2000 na prędkość obrotową . Odczyt prędkości może być dokonywany na wyświetlaczu jednostki sterującej .

1

ξ > 1

ξ ≤ 1

ξ = 1

Palnik

Kocioł

Regulator

Pomiar ( czujnik )

Przetwornik

Węzeł porównujący

Zadajnik

Przełącznik rodzaju pracy

---