2.Ruch jednostajny:
;

;

ruch jednostajnie przyspieszony a=const

;

rów. Torricellego;

3. Zasady dynamiki Newtona

I. Każde ciało na które nie działa żadna siła albo oddziałujące siły się równoważą, porusza się ruchem jednostajnym prostoliniowym.

II.
; III.

4.Inercjalne i nie inercjalne układy odniesienia Układy w których obowiązują zasady dynamiki Newtona nazywamy układami inercjalnymi, a układy w których nie obowiązują układami nie inercjalnymi.

- układy inercjalne to takie układy odniesienia, które spoczywają lub poruszają się ruchem jednostajnym prostoliniowym.

-układy nie inercjalne poruszają się ruchem jednostajnie przyspieszonym.

Transfor. Galileusza:
; w przypadku gdy v jest równoległe do osi X a r₀ = 0 mamy:
;
;
Ale układ O' może być także obrócony (przemieszczony i obrócony): ogólna postać transformacja Galileusza

gdzie: R - macierz obrotu, v - prędkość układu, r₀ - położenie początkowe

5. Siła bezwładności.: Obliczając dwukrotną pochodna równania na trans. Galileusza otrzymamy
-trans. Galileusza

Nawet gdy
mamy
gdzie a₀ to przyśpieszenie układu. Zatem nawet, gdy na ciało nie działa (a=0) to na ciało dział siła nazywana siłą bezwładności.
Przykład: gwałtownie hamujący samochód, pociąg.

Efekt Coriolisa - efekt występujący w obracających się układach odniesienia. Objawia się zakrzywieniem toru ciał poruszających się w takim układzie. Zakrzywienie to zdaje się być wywołane jakąś siłą (dlatego efekt Coriolisa nazywany jest najczęściej siłą Coriolisa), w rzeczywistości jest jednak spowodowany ruchem układu odniesienia. Wartość tej siły wynosi:
;

a przyspieszenia

6.Praca.

Po scałkowaniu otrzymamy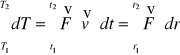

Wielkość W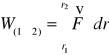
nazywamy pracą jaką należy wykonać przy przesunięciu ciała z punktu 1 do punktu 2. praca wykonana na drodze dr będzie równa:
W przypadku, gdy siła F jest stała i tworzy stały kąt
z przesunięcie otrzymujemy znany wzór na pracę siły F wykonaną przy przesunięciu ciała po drodze d:

Zmiana pracy w czasie jest to moc.
;
;

Gdy praca jest stała: P= const to
;

Jednostką mocy w układzie SI jest 1 Wat.

7.Energia kinetyczna

- II zasada dynamiki Newtona

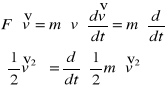
Wprowadźmy nową wielkość T :

Otrzymamy równanie
gdzie T to wielkość wyrażona w jednostkach energii w układzie SI - w Joulach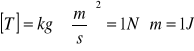
Energia potencjalna. Przekształcając wzór na prace otrzymamy zależność

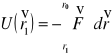
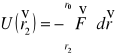
Praca wykonana przy przesunięciu ciała z punktu 1 do punktu 2 równa jest różnicy energii potencjalnej w tych dwóch punktach.

Energia potencjalna jest to:

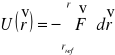
gdzie r_ref jest to punk odniesienia, dobierany tak, aby energia potencjalna w tym punkcie U(r_ref) = 0 była równa zero: U(r_ref) = 0. Energia potencjalna jest wielkością (funkcją) skalarną - tworzy pole skalarne. Należy zwrócić uwagę na znak w równaniu. Znak jest ujemy! U(r) - energia potencjalna w punkcie r jest równa pracy, jaką należy wykonać przeciwko sile F, aby przesunąć ciało z r_ref do r. Siła, z jaką musimy działać, jest równa co do wartości lecz ma przeciwny znak - stąd mamy znak minus

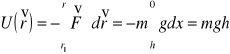
energia potencjalna w pobliżu powierzchni Ziemi.

8.Zasada zachowania energii.
po przekształceniu:

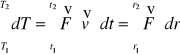
w wyniku otrzymamy:

lub

zależność T + U = const nazywamy ZZE. Zasada zachowania energii: w polu sił zachowawczych całkowita energia układu, równa sumie energii kinetycznej i potencjalnej, jest wielkością stałą.

9.Pęd, zasada zachowania pędu

;
; jeżeli
i
to p = const

Zasada zachowania pędu: jeżeli na układ nie działa żadna siła (lub działające siły się równoważą) to całkowity pęd układu nie ulegnie zmianie (jest zachowany).

Zderzenie elastyczne: dwie kule bilardowe zderzają się - nie tracąc energii. Spełnione są 2 zasady zachowania:

ZZP

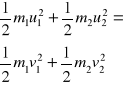
ZZE

10.Moment pędu

Moment pędu

Moment siły
; otrzymujemy zależność

Jest to II zasada dynamiki dla ruchu obrotowego.

Zasada zachowania momentu pędu

;
;

Jeżeli całkowity moment siły działającej na układ jest równy zero to całkowity moment pędu układu nie ulegnie zmianie (jest zachowany). Jest to treść zasady zachowania momentu pędu.

11.Pole grawitacyjne. Prawo powszechnego ciążenia.

Pole grawitacyjne to pole wytwarzane przez obiekty posiadające masę. Podstawową teorią opisującą pole grawitacyjne i jego związek z cechami przestrzeni jest ogólna teoria względności, stworzona przez Alberta Einsteina.

Energia potencjalna pola grawitacyjnego (prawo powszechnego ciążenia): (siła-wektor)

G- stała grawitacji

Grawitacja źródłem jest istnienie masy, jedno z najsłabszych oddziaływań, słabe natężenie(10^-36 - 10^-40),zasięg ∞

Energia potencjalna (skalar):

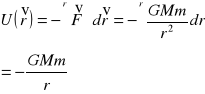
potencjał pola grawitacyjnego (skalar):

natężenie pola grawitacyjnego (wektor):

Bardzo ważną cechą siły grawitacyjnej jest to, że jest siłą zachowawczą, a zatem praca w polu siły ciężkości nie zależy od kształtu i długości drogi, lecz od położenia punktów początkowego i końcowego

Co to jest pole zachowawcze?

Praca wykonana po dowolnej drodze zamkniętej (punk końcowy pokrywa się

punktem początkowym) jest równa zero.

Prawa Keplera

I. planety krążą wokół Słońca po elipsach o

Parametrach p = L²/GMm i mimośrodzie ɛ = (1 + 2Ep / GMm )^1/2

II. prędkość polowa ruchu planet jest stała. Promień wodzący łączący Słońce, umieszczone w jednym z ognisk elipsy, z planetą, w jednakowych odstępach czasu zakreśla jednakowe pola. Konsekwencja zasady zachowania momentu pędu.

III.

12. Bryła sztywna - moment bezwładności

Moment bezwładności to miara bezwładności ciała w ruchu obrotowym. Im większy moment, tym trudniej zmienić ruch obrotowy ciała, np. rozkręcić dane ciało lub zmniejszyć jego prędkość obrotową.

Dla ciał o ciągłym rozkładzie masy sumowanie we wzorze na moment bezwładności przechodzi w całkowanie. Niech ciało będzie podzielone na nieskończenie małe elementy o masach dm, oraz niech r oznacza odległość każdego takiego elementu od osi obrotu. W takim przypadku moment bezwładności określa wzór

gdzie całkowanie odbywa się po całej objętości ciała

13.Energia kinetyczna bryły sztywnej

Gdy bryła sztywna obraca się względem jednej osi, otrzymujemy znany wzór

14.Równanie dynamiki ruchu obrotowego

gdzie

ɛ - przyspieszenie kątowe M - moment siły,

I - moment bezwładności

Porównanie: ruch postępowy i ruch obrotowy

Wzór na prędkość, przyspieszenie, moment pędu

energia kinetyczna

15.Oscylator harmoniczny:

Aby zaistniał ruch potrzebna jest siła :

F = -kx (x-wychylenie, k-sprężystość ukł)

m*a = -kx , to a + k/m x =0 , a -przyspieszenie

Możemy również zapisać :

x(t) = Asin (ωt + f₀)

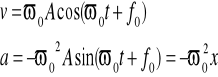
a stąd:

A - amplituda drgań

ωt +f₀ - faza drgań

ω₀ - prędkość kołowa , pulsacja , częstość

16. Oscylator tłumiony :W rzeczywistym oscylatorze w wyniku działania tarcia amplituda drgań maleje stopniowo aż do zera.

F = ma lub -kx - b(dx/dt) =m(d²x/dt²)

-b(dx/dt) - siła tłumiąca, jeżeli b jest mała:

lne^βT = βT - log. deklement tłumienia

β = r/2m - współczynnik tłumienia

17.Zjawisko rezonansu, występowanie rezonansu

Gdy ω=ω₀ , czyli gdy częstość siły wymuszającej równa się częstotliwości drgań własnych, w przypadku słabego tłumienia, gdy współczynnik tłumienia dąży do zera y → 0, a τ → ∞, z równania

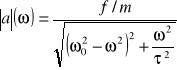
otrzymujemy, że amplituda a dąży do nieskończoności, a realnie do dużych, bądź bardzo dużych wartości:

Zjawisko to nosi nazwę rezonansu i odgrywa bardzo dużą rolę w układach mechanicznych, elektrycznych i magnetycznych.

1.Postulaty szczególnej teorii względności

Szczególna teoria względności oparta jest na dwóch postulatach:

1.prawa fizyki są takie same we wszystkich inercialnych układach odniesienia,

2.prędkość światła c jest stała i nie zleży od prędkości źródła.

Postulat 1 oznacza, że wszystkie inercjalne układy odniesienia są takie same, nierozróżnialne. Postulat 2 mówi, że prędkość świtała c jest uniwersalną stałą, jak stała grawitacji G czy ładunek elementarny e. Według ostatnich pomiarów prędkość światła (w próżni) wynosi: C = 299 792 458 ± 1.2 m/s.

2. Transformacja Lorentza

Weźmy pod uwagę dwa układy inercjalne S i S`, których osie x i x` są do siebie równoległe, a początki O i O` pokrywają się w układzie S ze stałą prędkością v , zwróconą zgodnie ze zwrotem osi x. Gdy pewne zdarzenie zaobserwowane w układzie S ma współrzędne x,y,z,t, to odpowiednie jego współrzędne w układzie S` wynoszą x`,y`,z` ,t`. Układy odniesienia wybieramy w taki sposób, żeby zawsze y` = y i z` = z i tymi współrzędnymi nie będziemy się zajmować. Mamy więc w każdym układzie jedną współrzędną przestrzenną (x lub x`) i jedna współrzędną czasową (t lub t`).

Równanie czoła fali kulistej :

x²+y²+z²=c²t²

x'²+y'²+z'²=c²t'²

stosuję podstawienia

x' = x - v t

y' = y

z' = z

t' = t + f x

c't' - promień kuli

podstawiam wartości i rozwiązuję układ równań , przy czym 2c²f + 2v = 0 ⇒

f = -(v / c²) , współczynnik

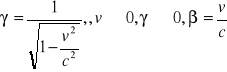
x' = γ( x - v t) x = γ( x' +vt')

y' = y y = y'

z' = z z = z'

t' = γ( t - (v/c²)x) t = γ( t'- (v/c²)x')

3. Efekty relatywistyczne: skrócenie długości

mamy dwa układy s i s', mierzymy długość w obydwu układach : l'- długość zmierzona przez obserwatora w ruchomego ,l- opisuje długość jaką zaobserwuje obserwator nie będący w ruchu ,gdzie :

l₀ = x₂ - x₁ , l' = x₂' - x₁'

l₀=x² - x¹= γ(x₂'+vt')-γ(x₁'+vt') =γ(x₂'-x₁')

l'=l₀/γ =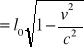
ciało obserwowane w ruchu jest „krótsze” od ciała w spoczynku

dylatacja czasu - Korzystając z transformacji Lorentza (i transformacji odwrotnej) możemy zapisać różnicę współrzędnych dwóch zdarzeń w czasoprzestrzeni:



Zakładamy, że zegar znajduje się w układzie „nieruchomym” O i spoczywa w tym układzie (Ax = 0). Drugi zegar spoczywa w poruszającym się układzie O'(Ax'=0). Związek między różnicami w czasie dwóch (tych samych) zdarzeń, zarejestrowanych w układach O i O', otrzymamy z równania (2.2.1):

Jest to równanie opisujące zjawisko relatywistycznej dylatacji czasu. Czas ∆t^` zmierzony w poruszającym się układzie O' jest większy od czasu ∆t zmierzonego w nieruchomym układzie O. W teorii względności efekt polegający bądź na opóźnianiu się zegara będącego w ruchu w stosunku do zegara spoczywającego w pewnym inercjalnym układzie odniesienia (kinematyczna dylatacja czasu), bądź na opóźnianiu się zegara znajdującego się w silnym polu grawitacyjnym (grawitacyjna dylatacja czasu); oba te efekty zostały zaobserwowane: poruszające się z dużymi prędkościami nietrwałe cząstki elementarne (np. w promieniowaniu kosm.) żyją dłużej niż cząstki spoczywające, natomiast czułe zegary znajdujące się w górach spieszą się w stosunku do zegarów pozostawionych na poziomie morza (będących w silniejszym polu grawitacyjnym — bliżej środka Ziemi).

dodawanie prędkości: Niech układ O' porusza się z prędkością V₁ (skierowaną wzdłuż osi X układy O, rys. 1.4), a w układzie O' punkt x' porusza się z prędkością v₂. Prędkość punktu x' względem nieruchomego układu O będzie równa:

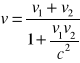
Składając prędkości nigdy nie przekroczymy prędkości światła. Gdy prędkości są małe, w porównaniu z prędkością światła, z równania otrzymujemy klasyczna wartość: v= V₁+V₂

4. Masa relatywistyczna: m. = γm₀ - masa ciała kiedy się porusza, nie jest równa masie ciała kiedy jest w spoczynku. Zmiana masy jest wynikiem płynięcia czasu w dwóch układach. Energia relatywistycna: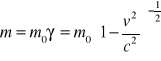

gdzie: m - masa relatywistyczna, m0 - masa spoczynkowa

V - małym:

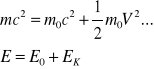
m - całkowita masa jest cał. energią zawartą w masie, m₀c² - energia spoczynkowa, 1/2m₀V² - prędkość ruchu, E - energia całkowita, E₀ - energia spoczynkowa,

Pęd relatywistyczny Pęd jest funkcją prędkości. Jeżeli działa stała, ciało przyśpiesz. Gdy dochodzimy do prędkości bliskich prędkości światła, masa ciała zaczyna rosnąć. Aby przyspieszyć ciała o niezerowej masie spoczynkowej do prędkości światła, musimy posłużyć się nieskończoną siłą!

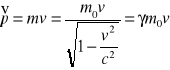
5. Energia relatywistyczna m² c⁴ =m₀² c⁴ +m² v² c²

E² =m₀² c⁴ +p² c² jest o fundamentalny związek między energią, masą a pędem relatywistycznym. W mechanice relatywistycznej masa jest równoważna energii, a energia jest równoważna masie. W przypadku ciała nieruchomego, p = 0, równie sprowadza się do słynnego wzoru: E = m₀c²

6. Deficyt masy. Weźmy jądro o masie Mj, utworzone przez Z protonów, (A - Z) neutronów definiuje się jako:

Jest to suma składników minus masa produktu (jądra atomu). ∆M > 0 ! Brakująca masa, a raczej równoważna tej masie energia, wiąże nukleony (neutrony i protony) w jądrze. Energia wiązania wynosi, zgodnie z ∆E = ∆m₀c²

7. Źródło energii: reakcje rozpadu Jądro uranu U 235 po trafieniu neutronem staje się niestabilne i rozpada się na dwa jądra potomne, pewną licz cząstek, oraz ogromną ilość energii. Wśród

cząstek produkowanych w reakcji są 2 lub 3 neutrony.Jądra uranu U ₂₃₅ ale także plutonu Pu ₂₃₉, toru (Tr ₂₃₂) ulegają tym reakcjom spontanicznie. Takie zjawisko nazywany spontanicznym

rozszczepieniem. Jeżeli stężenie uranu jest dostatecznie wysokie, aby wytworzone neutrony trafiły w kolejne jądra uranu, wtedy mamy do czynienia z reakcją łańcuchową. Raz zapoczątkowana reakcja łańcuchowa będzie trwać

dopóki będą jądra uranu. Nie da się jej przerwać ani zatrzymać. Ilość energii wytwarzanej w reakcji rozszczepienie jednego jądra U 235 to ~ 200 MeV.

8. Źródło energii: reakcje fuzji W reakcji fuzji jądra łączą się tworząc w wyniku jądro, szereg cząstek i bardzo duże ilości energii. Masa produktów reakcji jest mniejsza niż masa składników, różnica jest czystą energią.

Oto kilka przykładowych reakcji fuzji:

(1) D + T—» He (3.5 Me V) + n (14.1 Me V)

(2i) D + D —» T (1.01 MeV) + p (3.02 MeV)

(2ii) —» He (0.82 MeV) + n (2.45 MeV)

3. D + He —» He (3.6 MeV) + p (14.7 MeV)

4. T + T —» He + 2 n + 11.3 MeV

(5) He + He —» He + 2 p + 12.9 MeV

1.Elektro statyka. Prawo Coulomba Weźmy dwa ładunki q1, q2 odległe od siebie o r. Siły działające między dwoma ładunkami. k - stała Coulomba

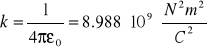
W próżni postać prawo Coulomba przyjmie postać

W ośrodku różnym od próżni musimy uwzględnić przenikalność ośrodka, stąd

przenikalność elektryczna próżni

względna przenikalność elektryczna ośrodka

Należy pamiętać, o związku między elektrycznymi i magnetycznym własnościami próżni a prędkością światła: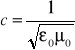

E₀ to podatność elektryczna, u₀ podatność magnetyczna próżni.. Oddziaływanie elektryczne ładunków zależy od ośrodka, w którym ładunki się znajdują. Ośrodek wpływa na oddziaływanie, ale też pole elektryczne oddziałuje na ośrodek (polaryzacja elektryczna ośrodka)

2.Pole elektryczne: natężenie i potencjał, indukcja pola elektrycznego Pole elektryczne definiuje się jako siłę na jednostkę ładunku
E - natężenie pola elektrycznego, F - siła z prawa Coulomba, q ładunek próbny. Równanie to jest prawdziwe tylko w przypadku, gdy ładunki są nieruchome (elektrostatyka). Jeżeli ładunki się poruszają, zależność między siła a natężeniem pola elektrycznego opisuje prawo Lorentza.

W przypadku, gdy mamy bardzo dużą (praktycznie nieskończoną) liczbę ładunków, to równanie przyjmuje postać równania całkowego:

Pole elektryczne jest polem zachowawczym - praca wykonana przez pole elektryczne nie zależy od drogi, lecz od położeń punktu początkowego i końcowego. Dlatego praca wykonana dla drogi zamkniętej jest równa zero.
Energię potencjalną w punkcie r, czyli U(r) definiujemy jako:

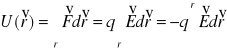
jest to praca wykonaną przez siły zewnętrzne przy przenoszeniu ładunku punktowego q z nieskończoności do punktu r.

Indukcja pola elektrycznego Jak będzie wyglądało pole elektryczne w ośrodku różnym od próżni: w cieczach, gazach, czy ciałach stałych, czyli ośrodkach charakteryzujących się różną od jedności względną przenikalnością elektryczną.

Pole elektryczne definiujemy w takich ośrodkach poprzez wektor indukcji pola elektrycznego D w sposób następujący:

D - wektor indukcji pola elektrycznego, E - wektor natężenia pola elektrycznego, ɛ - przenikalność elektryczna ośrodka.

3. Prawo Gaussa Strumień pola elektrycznego, w ośrodku o przenikalności elektrycznej ośrodka ɛ , definiujemy następująco:

0_E- strumień pola elektrycznego, D, E - wektory pola elektrycznego, A powierzchnia zamknięta.

Prawo Gaussa (postać całkowa):

A - powierzchnia obejmująca objętość V. Strumień pola elektrycznego przechodzącego przez dowolną powierzchnię zamkniętą jest proporcjonalny do całkowitego ładunku elektrycznego zamkniętego przez tą powierzchnię. Prawo Gaussa (postać różniczkowa):

p jest to gęstość ładunku [C/m ]

4.Praca pola elektrycznego, napięcie i potencjał

Praca wykonana przy przesunięciu ładunku między dwoma punktami wynosi:

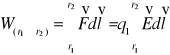
Pole elektryczne jest polem zachowawczym. Praca wykonana po dowolnej drodze zamkniętej równa się zero.

5.Dipol elektryczny. Polaryzacja. Własności elektryczne materii Dipol elektryczny: układ dwóch ładunków: +q i -q odległych o stałą odległość d. Moment dipolowy cząsteczki jest zdefiniowany jako:
Potencjał dipola elektrycznego zapisujemy następująco

Materię dzielimy, ze względu na to jak reaguje na przyłożone zewnętrzne pole elektryczne, na dwie główne grupy: dielektryki (ɛ >= 1) He, H₂, N₂; paraelektryki (ɛ >> 1) H₂O, etanolC₂H₅OH;

ferroelektryki.

Dielektryki tworzą materiały, zbudowane z cząsteczek niepolarnych, czyli cząsteczek, które nie posiadają trwałych elektrycznych momentów dipolowych. Obecności pola elektrycznego powoduje indukowanie momentu dipolowego, poprzez przesunięcie środków ciężkości ładunków dodatnich i ujemnych. Zjawisko to nosi nazwę polaryzacji elektronowej. Pole elektryczne porządkuje jednocześnie dipole elektryczne zgodnie z zwrotem pola. Jest to polaryzacja kierunkowa.

Cząstki niepolarrne to cząstki o budowie symetrycznej, jak: H2, N2, O2, czy gazy szlachetne. Paraelektryki to materiały, których cząsteczki posiadają trwały elektryczny moment dipolowy (cząstki polarne) również w nieobecności pola elektrycznego. Doskonałym przykładem jest cząsteczka wody (H₂O). W nieobecności zewnętrznego pola elektrycznego paraelektryki nie wykazują pola elektrycznego, ponieważ dipole elektryczne są zorientowane w sposób przypadkowy, chaotyczny, i pola dipoli wzajemnie się znoszą.

Trzeci rodzaj materii: ferroelektryki, są materiały wykazujące pole elektryczne w nieobecności zewnętrznego pola elektrycznego.Charakterystyczną cechą ferroelektryków jest struktura domenowa, co powoduje np. występowanie histerezy.Analogicznie, w przypadku pola magnetycznego materię dzielimy na diamagnetyki, paramagnetyki, ferromagnetyki.

6.Przepływ prądu. Prawo Ohma (postać zwykła i różniczkowa) U =I * R ; U - napięcie (różnica potencjałów) [V - volt], I - natężenie prądu [A - amper], R - stała, opór w jednostkach [Q - ohm]

Różniczkowe prawo Ohma: dI = dU / R.

Napięcie i natężenie prądu płynącego obwodzie są zgodne w fazie. Związek między napięciem a natężeniem prądu podaje prawo Ohma: I = U / R Prąd elektryczny - uporządkowany ruch ładunków. Definiujemy go poprzez wielkość zwaną natężeniem prądu elektrycznego, który jest równa: I = dQ / dt .

Natężenie prądu jest równe ilorazowi ładunku elektrycznego, jaki przepłynął przez powierzchnię, do czasu przepływu. W układzie SI jednostki są następujące 1A = 1C / s

7.Opór, zależność temperaturowa oporu, łączenie oporników opór R nie jest stały, ale w istocie zmienia się liniowo w funkcji temperatury:

R(T) = R₀ (1 + α(T - T₀)) ;

gdzie R₀ to opór materiału w temperaturze T₀.

Dla przewodnika o długości l, przekroju poprzecznym S, jego opór R będzie równy:

p to opór właściwy [Ω m] wartość charakterystyczna materiału, z którego wykonano przewodnik. Prawa Kirchoffa:

I.

suma prądów wpływających i wypływających z węzła sieci jest równa zero.

II.

W oczku sieci suma sił elektromotorycznych i spadków napięć jest równa zero (ZZE)

Łączenie szeregowe oporników

Opór zastępczy układu N szeregowo połączonych oporników jest równy:

Łączenie równolegle oporników

Opór zastępczy układu N równolegle połączonych oporników jest równy:

8.Kondensatory Parametr charakteryzujący kondensator to pojemność kondensatora: C = Q / U jednostki 1F - Farad = 1 Coulomb/ V

Kondensatory magazynują energię w postaci pola elektrycznego. Praca przy umieszczeniu ładunku dq na kondensatorze o napięciu U wynosi:

dW = Udq = CU dU ; Dlatego energia naładowania kondensatora o pojemności C i napięciu U jest równa: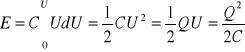
Energia kondensatora jest równa pracy wykonanej przy ładowaniu kondensatora.

Kondensator płaski o powierzchni okładek S, odległych o d, wypełniony dielektrykiem ɛ ma pojemność:

Kondensator kulisty o promieniach R1 i R₂, wypełniony dielektrykiem ɛ ma pojemność:

łączenie kondensatorów analogicznie jak oporniki

9.Pole magnetyczne 10.Siła Lorentza. Przewodnik z prądem w polu magnetycznym

Dwa równoległe przewodniki, przez które płynie prąd, przyciągają się lub odpychają się. Można więc przyjąć, że w przestrzeni otaczającej przewodnik z prądem znajduje się pole magnetyczne. Pole to opisujemy za pomocą wektora indukcji magnetycznej
, zdefiniowanego przez siłę elektrodynamiczną działającą na poruszający się ładunek:

Pole magnetyczne jest polem bezźródłowym , jest polem wirowym. Nie mam szans na otrzymanie pojedynczego bieguna N lub S .

Siła działająca na przewodnik z prądem I:

lub
Wiadomo, że indukcja pola magnetycznego jest proporcjonalna do natężenia prądu i odwrotnie proporcjonalna do odległości:

μ₀ - przenikalność magnetyczna próżni

w próżni

11.Prawo Ampera. Prawo Biot - Savarta

Istnieją dwie metody wyznaczenia pola magnetycznego: prawo Biot - Savarta i prawo Ampera. I. Prawo Biot - Savarta (postać różniczk.)

Natężenie pola magnetycznego wytwarzanego w odległości r od elementu dl wynosi:

zaś indukcja pola magnetycznego

II. Prawo Ampera Prawo Ampera wiąże cyrkulację (krążenie) pola magnetycznego po konturze zamkniętym l z natężeniem prądu przechodzącego przez powierzchnię wyznaczoną przez tenże kontur l.

12.Prawo Gaussa dla pola magnetycznego

Analogicznie do pola elektrycznego, możemy sformułować prawo Gaussa dla pola magnetycznego
lub

13.Dipol magnetyczny, magnetyzacja, własności magnetyczne materii

Dipol magnetyczny definiujemy jako pole magnetyczne wytwarzane przez obwód kołowy, w którym płynie prąd I:

Na dipol magnetyczny znajdujący się w polu magnetycznym działa moment siły równy

Energia potencjalna dipola magnetycznego jest równa:
Diamagnetyki to materiały o zerowym dipolowym momentem magnetycznym w nieobecności zewnętrznego pola magnetycznego. Obecność zewnętrznego

pola magnetycznego indukuje prąd na orbicie atomu; prąd, który tak płynie, aby wytworzony przez nie pole magnetyczne było przeciwnie skierowane do przyłożonego, zewnętrznego pola magnetycznego. Jest to atomowa wersja reguły Lentza: indukowane pole magnetyczne sprzeciwia się polu magnetycznemu, które go wytworzyło.

Paramagnetyki, zawierają niezerowe momenty dipolowe magnetyczne. Powoduje to, że ich magnetyzacja jest proporcjonalna do przyłożonego pola magnetycznego (B), a odwrotnie proporcjonalna do temperatury (T). Jest to

prawo Curie: M = C (B/T)

gdzie: C - stała Curie, M - magnetyzacja

Ferromagnetyki, to materiały, będące szczególnym rodzajem paramagnetyków. O ile w paramagnetykach, dipole magnetyczne są ułożone losowo, to w ferro magnetykach istnieje oddziaływanie długo zasięgowe, które porządkuje ułożenie momentów magnetycznych w specyficzny sposób. Wynikiem istnienia oddziaływania długo zasięgowego jest powstanie struktury domenowej w całej objętości materiału, co dalej skutkuje zjawiskiem histerezy magnetycznej.

14.Indukcja elektromagnetyczna, prawo Faradaya Prawo Faradaya mówi, że cyrkulacja pola elektrycznego wywołana jest zmianą pola magnetycznego:

Po podstawieniu definicji strumienia pola magnetycznego otrzymamy następującą postać prawa Faraday'a:

gdzie kontur C obejmuje powierzchnię A. Jest to postać całkowa prawa Faraday'a. Postać różniczkowa wygląda następująco:

Prawo Faradaya mówi, że zmiana pola magnetycznego powoduje powstanie pola elektrycznego

15.Równania Maxwella Równania Maxwella: zbiór czterech równań, opisujących zachowanie pola elektrycznego i magnetycznego oraz ich oddziaływani e z materią. 1. prawo Gaussa (dla pola elektrycznego) postać różniczkowa:
Postać całkowa:
2. prawo Gaussa (dla pola magnetycznego) postać różniczkowa
Postać całkowa

3. Prawo Faradaya

postać różniczkowa

Postać całkowa:

4. prawo Ampera (uzupełnione przez Maxwella)

Postać różniczkowa:

Postać całkowa: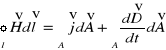

Pierwsze równanie Maxwella: pole elektryczne jest polem źródłowym, istnieją ładunki elektryczne.

Drugie równanie Maxwella: pole magnetyczne jest polem bezźródłowym, nie istnieją monopole magnetyczne.

Trzecie równanie Maxwella to prawo Faradaya o indukcji. Zmienne pole magnetyczne powoduje powstanie pola elektrycznego.

Czwarte równanie Maxwella to prawo Ampera z dodanym członem odpowiedzialnym za tzw. prąd przesunięcia. Prądy i zmienne pole elektryczne powodują powstanie pola magnetycznego.

E - natężenie pola elektrycznego

D - indukcja pola elektrycznego

H - natężenie pola magnetycznego

B - indukcja pola magnetycznego

j - gęstość prądu p - gęstość ładunku

---