ZESTAW A Prawo Ampera i wzór Ampera

Obliczmy całkę krzywo liniową
po konturze zamkniętym C (w naszym przypadku po okręgu o promieniu r) wokół nieskończenie długiego prostoliniowego przewodnika z prądem. Ponieważ linie sił pola magnetycznego pochodzącego od prądu prostoliniowego tworzą w płaszczyźnie prostopadłej do przewodnika okręgi koncentryczne o środkach leżących na przewodniku. Indukcja
we wszystkich punktach okręgu jest taka sama i wynosi :
, a kierunek wektora
pokrywa się ze styczną do okręgu.

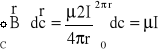
Wzór jest również prawdziwy dla konturu zamkniętego C dowolnego kształtu obejmującego przewodnik. Co więcej wynik całkowania jest taki sam, gdy przewodnik (nie jest prostoliniowy) ma dowolny kształt. Jeżeli kontur C nie obejmuje przewodnika z prądem, to cyrkulacja z wektora indukcji
po tym konturze jest równa zero.

Jeżeli kontur C obejmuje kilka przewodników z prądem to wobec zasady superpozycji pól magnetycznych wzór można zapisać: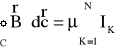
gdzie N- ilość przewodników z prądem obejmowanych przez kontur C . Wzór ten wyraża matematyczną postać prawa Ampera. Całka okrężna (po obwodzie zamkniętym) występująca w tym prawie nosi nazwę cyrkulacji albo krążenia wektora
.

Wiedząc, że
= μ.
możemy zapisać: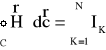
W tym przypadku prawo przepływu prądów tzw. prawo Ampera można sformułować następująco: Cyrkulacja wektora natężenia pola magnetycznego jest równa algebraicznej sumie natężeń prądów płynących wewnątrz konturu obejmującego te prądy.

Rozkład Maxwella. Ten angielski fizyk na podstawie założeń teorii kinetycznej gazu wyprowadził prawo rozkładu wartości prędkości poruszających się cząsteczek. Ma ono postać: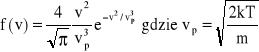
nosi nazwę prędkości najbardziej prawdopodobnej . Funkcja f(v) określa prawdopodobieństwo , że na ogólną liczbę cząsteczek N, liczba dN cząsteczek ma prędkości zawarte w elementarnym przedziale od v do v+dv. Zatem

Założenia kinetycznej teorii gazu doskonałego. Z mikroskopowego punktu widzenia gaz doskonały możemy też zdefiniować , czyniąc pewne założenia o własnościach cząsteczek gazów rzeczywistych. Mianowicie: 1. Cząsteczki danego gazu można traktować jako punkty materialne o równych masach, 2. Cząsteczki gazu znajdują się w szybkim chaotycznym ruchu. Chaotyczność ruchu oznacza , że cząsteczki poruszają się we wszystkich kierunkach , jakie są tylko możliwe , i że żaden z tych kierunków nie jest uprzywilejowany, 3. Cząsteczki gazu zderzają się sprężyście ze sobą i ze ściankami naczynia . Siły działające podczas zderzenia są siłami zachowawczymi i wobec tego energia mechaniczna cząsteczek pozostaje stała, 4. Siły działają tylko w momencie zderzenia się cząsteczek gazu. Cząsteczki oddalone od siebie nie działają na siebie żadnymi siłami, 5. Objętość cząsteczek gazu jest zaniedbywalnie mała w porównaniu z objętością zajmowaną przez gaz.

Inercjalne układy odniesienia. Transformacja Galileusza

Z pierwszej zasady dynamiki wynika, że jeśli na ciało nie działają żadne siły lub działają siły zrównoważone (F=0), to ciało jest nieruchome lub porusza się ruchem jednostajnym prostoliniowym. Ponieważ ruch jest zmianą położenia ciała względem układu.

Otóż okazuje się, że zasada ta obowiązuje tylko w inercjalnych układach odniesienia. Układy odniesienia, w których I zasada dynamiki nie jest spełniona, noszą nazwę układów nieinercjalnych. Pierwsza zasada dynamiki jest w istocie postulatem, że układ inercjalny

istnieje.

Rozpatrzmy dwa układy odniesienia jeden nieruchomy O i drugi O' poruszający się względem układu (J ruchem jednostajnym prostoliniowym x. prędkością v₀. Układy te orientujemy tak, aby osie x i x` pokrywały się i aby kierunek tych osi pokrywał się z kierunkiem ruchu układu O'.

Przyjmujmy ponadto, że osie y i y' oraz z i z' są. do siebie równoległe oraz że w chwili t=0 układy pokrywają się.

Załóżmy, że chcemy opisać ruch punktu materialnego P z punktu widzenia obserwatora związanego z układem O i obserwatora związanego /. układem O'.

Dwa układy odniesienia O i O' poruszają się względem siebie mchem jednostajnym prostoliniowym. Prędkość poruszającego się ciała jest w obu układach różna, natomiast przyspieszenie jest jednakowe. x'=x-v_ot y'=y z'=z Przyjmiemy ponadto, że w obydwu układach odniesienia czas płynie jednakowo, tzn. t'=t Zależności te noszą nazwę transformacji Galileusza.

Pierwsza zasada dynamiki głosi, że ciało nie poddane działaniu żadnej siły albo poddane działaniu sił równoważących się pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. Pierwsza zasada dynamiki nosi nazwę zasady bezwładności. Przez bezwładność rozumiemy właściwość ciała decydującą o tym, że ciało bez działania sił nie może zmienić ani wartości, ani kierunku swej prędkości. Czyli bez działania sil pozostaje w takim stanie jak było wcześniej; spoczywa jeśli spoczywało, lub porusza się ruchem jednostajnym jeśli było w jakimkolwiek ruchu.

Druga zasada dynamiki głosi, że: przyspieszenie ciała a jest wprost proporcjonalne do siły F, która to przyśpieszenie wywołuje: F = ma

Trzecia zasada dynamiki zwana również zasadą akcji i reakcji, dotyczy wzajemnego oddziaływania dwóch ciał (względnie układów ciał). Głosi, że jeżeli ciało A działa na ciało B siłą
a ciało B działa na ciało A siłą
równą co do wartości, lecz przeciwnie skierowaną: Fab=-Fba

ZESTAW B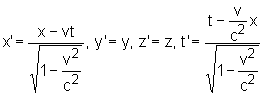

Lorentza transformacja, Lorentza przekształcenie, przekształcenie matematyczne opisujące transformacje wielkości fizycznych w czasoprzestrzeni czterowymiarowej przy przechodzeniu od jednego inercjalnego układu odniesienia, określonego przez współrzędne przestrzenne x, y, z i współrzędną czasową t, do drugiego, określonego przez współrzędne x', y', z' oraz t'. W najprostszym przypadku, jeśli układ (x', y', z', t') porusza się jednostajnie w kierunku osi x z prędkością v, to transformacja Lorentza ma postać: gdzie c - prędkość światła w próżni.
transformacji Lorentza wynikają wszystkie efekty kinematyczne szczególnej teorii względności, takie jak: reguła sumowania się prędkości prowadząca do niemożności uzyskania prędkości większej od prędkości światła, względność pojęcia równoczesności, skrócenie Lorentza-Fitzgeralda, spowolnienie biegu poruszających się zegarów.
Nieinercjalny układ odniesienia, fizyczny układ odniesienia, w którym nie jest spełniona I zasada dynamiki Newtona: np. układ związany z obracającym się ciałem (w szczególności układ związany z Ziemią) lub ciałem poddanym przyspieszeniom liniowym. Przeciwieństwo układu odniesienia inercjalnego. W nieinercjalnym układzie odniesienia obserwuje się np. siłę Coriolisa, siłę odśrodkową, inne siły bezwładności.

Siły bezwładności, pozorne siły działające na ciała fizyczne w nieinercjalnych układach odniesienia (styczna siła bezwładności, siła odśrodkowa, siła Coriolisa). Liczbowo siły bezwładności równe są iloczynowi masy i odpowiedniego przyspieszenia, a skierowane przeciwnie niż siła wymuszająca ruch
Coriolisa siła, jedna z sił bezwładności działająca na ciało znajdujące się w nieinercjalnym (tu: obracającym się) układzie odniesienia, F_cor = -2m ω×v, gdzie m - masa ciała, ω - wektor prędkości kątowej obracającego się układu, v - wektor prędkości liniowej ciała mierzony w obracającym się układzie odniesienia .Siła Coriolisa spowodowana dziennym ruchem obrotowym działa na poruszające się poziomo na Ziemi ciała, osiągając największe wartości na biegunach (przy ruchu poziomym wektory ω i v są prostopadłe, niezależnie od kierunku v), a jej składowa pozioma zanika na równiku. Na półkuli północnej powoduje odchylanie się poruszających się poziomo ciał na prawo (odpowiedzialne np. za intensywniejsze podmywanie prawych brzegów rzek), a na półkuli południowej - w lewo. Siła Coriolisa działa na spadające swobodnie ciała, odchylając je od pionu w kierunku wschodnim. Siła działająca na jednostkową masę nazywa się przyspieszeniem Coriolisa.

Ciśnienie w cieczy i gazie . Prawo Pascala.

Ciecze i gazy noszą łączną nazwę płynów . Ciśnienie płynu można scharakteryzować wielkością siła działających na siebie poszczególnych warstw płynu lub na stykające się z nimi ciała . Stosunek siły parcia na dowolną powierzchnię w płynie do wielkości tej powierzchni nazywamy ciśnieniem . Jednostką ciśnienia jest paskal (Pa). Jest to ciśnienie jakie wywiera siła jednego niutona na powierzchnię 1 m² _--
Zjawisko to opisuje prawo Pascala, które można sformułować następująco: Ciśnienie zewnętrzne wywierane na ciecz lub gaz jest przenoszone we wszystkich kierunkach jednakowo.

p = p_o + δgh , gdzie δ gęstość cieczy, g - przyspieszenie ziemskie, h- głębokość mierzonego ciśnienia, p_o ciśnienie na powierzchni.

Prawo Archimedesa. Na ciało zanurzone w cieczy działa siła wyporu równa ciężarowi wypartej przez to ciało cieczy.

Pływanie ciał. Na każde ciało zanurzone w cieczy działa siła wyporu W = Vgδ_o i siła ciężkości Q = Vgδ - gdzie δ_o i δ oznaczają odpowiednio gęstość cieczy i średnią gęstość ciała niejednorodnego . Wypadkowa tych dwóch sił wyraża się wzorem R = W-Q = Vg(δ_o -δ).

Mogą tu wystąpić trzy przypadki: 1) δ>δ_o wówczas wypadkowa siła R<0 ciało będzie tonąć.

2) δ=δ_o - wówczas R=0 ciało będzie znajdować się w równowadze z cieczą na dowolnej głębokości zanurzenia, 3) δ<δ_o wówczas R>0 ciało będzie pływać częściowo zanurzone.

Prąd stały i prawa Ohma i Kirchoffa.

Przez przepływ prądu elektrycznego rozumiemy ruch ładunków elektrycznych. Czynnikiem wywołującym ten ruch jest istnienie napięcia, czyli różnicy potencjałów.

W każdym zamkniętym obwodzie prądu można wyróżnić źródło (czyli tzw. część wewnętrzną obwodu) wytwarzające różnicę potencjałów między dwoma biegunami, dodatnim i ujemnym, oraz odbiorniki prądu (czyli tzw. część zewnętrzną obwodu, utworzoną

z przewodników elektryczności).

Zgodnie z tradycją, za kierunki prądu w obwodzie zewnętrznym przyjmuje się kierunek od potencjału wyższego - dodatniego, do niższego - ujemnego

W czasie przepływu prądu przez przewodniki metalowe mamy do czynienia z ruchem swobodnych elektronów, a więc nośników prądu poruszających się od potencjału niższego do wyższego, czyli w kierunku przeciwnym do umownie przyjętegoPrzez natężenie prądu elektrycznego rozumiemy stosunek ładunku przepływającego przez poprzeczny przekrój przewodnika do czasu przepływu:
. W przypadku prądu stałego, tj. prądu płynącego w jednym kierunku, gdy jego natężenie jest stałe w czasie
. Jednostką natężenia prądu elektrycznego jest amper [A].

Prawo Ohma . Prawo Ohma mówi o prostej proporcjonalności prądu I płynącego przez przewodnik do napięcia U przyłożonego na jego końcach.
Prawo Ohma mówi, że stosunek napięcia U między dwoma punktami przewodnika do należenia I przepływającego przezeń prądu jest wielkością siała (R) i nie zależy ani od napięcia U, ani od natężenia I prądu. Opór elektryczny R (zwany też rezystancją) wyrażany jest w omach [Ω].

Prawa Kirchoffa. Pierwsze prawo Kirchoffa mówi, że w dowolnym punkcie W obwodu (w węźle) suma algebraiczna natężeń prądów stałych dopływających i odpływających do węzła równa się zeru.
Natężenie prądów dopływających do węzła uważamy za dodatnie, natężenie prądów odpływających za ujemne. Innymi słowy, w żadnym punkcie obwodu ładunki się nie gromadzą, nigdzie też nie giną, ani nic powstają (zasada zachowania ładunku). Ile ładunków do węzła dopływa, tyle w tym samym czasie z niego odpływa:

Drógie prawo Kirchoffa mówi, że w dowolnie wydzielonej zamkniętej części obwodu elektrycznego, w tzw. oczku, suma algebraiczna wszystkich napięć elektrycznych panujących na poszczególnych elementach oczka równa się zeru. Bierzemy tu pod uwagę wszystkie czynne siły elektromotoryczne (SEM) E, jak również wszystkie istniejące w tej części obwodu spadki napięć IR.

ZESTAW C

Ruch prostoliniowy. Prędkość ruchu.

Ruchem prostoliniowym nazywamy ruch ciała (punktu materialnego) po torze będącym linią prostą.
Prędkość średnia. Jeżeli w chwili t_o ciało zajmuje położenie A (współrzędna S₁), a w chwili 1₂ położenie B (współrzędna S₂), to prędkość średnia ruchu jest definiowana wzorem
. Prędkość średnia jest. więc ilorazem różnicowym drogi i czasu.
Prędkość chwilowa. Prędkość średnia nie określił dokładnie ruchu ciała. Prawdziwy obraz ruchu ciała. np. na odcinku AB leżącym wzdłuż osi Os ,otrzymamy, znajdując prędkość chwilową w każdym punkcie tego odcinka. Zatem prędkość chwilowa jest więc pochodną drogi względem czasu. Prędkość chwilową nazywamy też po prostu prędkością.
, ze wzoru tego wynika także , że przyrost drogi Δ S w czasie od 0 do t wyraża się całką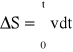

Ruch prostoliniowy jednostajny.

Jeżeli prędkość ciała jest stała (nie zależy od czasu), to ruch jest jednostajny. Ze wzoru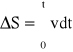
przy założeniu, że w chwili t=0, S=0, otrzymujemy wzór na drogę w ruchu jednostajnym prostoliniowym S=vt . Prędkość chwilowa w ruchu jednostajnym jest stała i równa prędkości średniej.

Ruch prostoliniowy zmienny. Przyspieszenie

Jeżeli prędkość ciała zależy od czasu, to ruch nazywamy zmiennym. Niech w chwili t₁ prędkość ciała wynosi v₁, a w chwili t₂ niech wynosi v₂. Przyspieszeniem średnim ruchu nazywamy iloraz różnicowy prędkości i czasu, co zapisujemy
. Przyspieszenie chwilowe, zwane krótko przyspieszeniem, jest pochodną prędkości względem czasu.

Ruch prostoliniowy jednostajnie zmienny.

Ruch, w którym przyspieszenie jest stałe (a=const), nazywamy mchem jednostajnie zmiennym. Jeżeli a>0, to ruch jest jednostajnie przyspieszony, jeżeli zaś a<0, lo ruch jest jednostajnie opóźniony. Przypadek a=0 określa ruch jednostajny. v = v_o + at , a draga określona jest wzorem :

Ruch krzywoliniowy

Załóżmy że w chwili t punkt znajduje się w punkcie A, a jego położenie określone jest przez wektor wodzący r(t). Po upływie czasu Δt punkt przemieści się po swym torze do punktu B, który jest określony przez wektor
. Droga, jaką przebyło ciało w tym czasie, wynosi ΔS. Iloraz różnicowy przyrostu wektora
przez czas Δt, w którym ten przyrost nastąpił określa wektor prędkości średniej
. Prędkość chwilowa wyraża się wzorem :
,

Ruch po okręgu jest szczególnym przypadkiem ruchu krzywoliniowego. Obierzmy układ współrzędnych 0_xy tak, aby początek układu znajdował się w środku koła o promieniu r. Droga kątowa. Położenie punktu A na okręgu można wtedy jednoznacznie określić za pomocą kąta ϕ: kątϕ nosi nazwę drogi kątowej. Jednostką drogi kątowej ϕjest radian. Drogę liniową s przebytą przez ciało po łuku koła można wyrazić za pomocą drogi kątowej następująco S = ϕr Oczywiście, aby wzór ten był prawdziwy droga ϕ musi być wyrażona w radianach.

Prędkość kątowa oznaczana jest przez
, a prędkość liniowa

Okres ruchu to czas T potrzebny na przebycie drogi kątowej ϕ = 2π. Dla ruchu jednostajnego po okręgu
.

Częstotliwością f ruchu po okręgu nazywamy liczbę obiegów punktu po okręgu w jednostce czasu ,
.

Przyspieszenie kątowe. Gdy ruch po okręgu jest niejednostajny, prędkość kątowa ulega zmianom, możemy wówczas wprowadzić nową wielkość charakteryzującą ruch, mianowicie przyspieszenie kątowe ε, które definiujemy jako pochodną, prędkości kątowej względem czasu:

Ciśnienie w cieczy i gazie . Prawo Pascala.

Ciecze i gazy noszą łączną nazwę płynów . Ciśnienie płynu można scharakteryzować wielkością siła działających na siebie poszczególnych warstw płynu lub na stykające się z nimi ciała . Stosunek siły parcia na dowolną powierzchnię w płynie do wielkości tej powierzchni nazywamy ciśnieniem . Jednostką ciśnienia jest paskal (Pa). Jest to ciśnienie jakie wywiera siła jednego niutona na powierzchnię 1 m² _--
Zjawisko to opisuje prawo Pascala, które można sformułować następująco: Ciśnienie zewnętrzne wywierane na ciecz lub gaz jest przenoszone we wszystkich kierunkach jednakowo.

p = p_o + δgh , gdzie δ gęstość cieczy, g - przyspieszenie ziemskie, h- głębokość mierzonego ciśnienia, p_o ciśnienie na powierzchni.

Prawo Archimedesa. Na ciało zanurzone w cieczy działa siła wyporu równa ciężarowi wypartej przez to ciało cieczy.

Pływanie ciał. Na każde ciało zanurzone w cieczy działa siła wyporu W = Vgδ_o i siła ciężkości Q = Vgδ - gdzie δ_o i δ oznaczają odpowiednio gęstość cieczy i średnią gęstość ciała niejednorodnego . Wypadkowa tych dwóch sił wyraża się wzorem R = W-Q = Vg(δ_o -δ).

Mogą tu wystąpić trzy przypadki: 1) δ>δ_o wówczas wypadkowa siła R<0 ciało będzie tonąć.

2) δ=δ_o - wówczas R=0 ciało będzie znajdować się w równowadze z cieczą na dowolnej głębokości zanurzenia, 3) δ<δ_o wówczas R>0 ciało będzie pływać częściowo zanurzone.
Prawo indukcji elekromagnetycznej Faradaya.

Zjawisko indukcji elektromagnetycznej polega na powstawaniu prądów elektrycznych wskutek zmian pola magnetycznego. Aby matematycznie ująć pojęcie indukcji należy wprowadzić pojęcie strumienia indukcji magnetycznej (strumienia magnetycznego) Φ_B który wyraża się wzorem
A więc prawo indukcji Faradaya mówi że: Indukowana w obwodzie SEM indukcji ε_ind jest równa co do wartości bezwzględnej a przeciwna co do znaku prędkości zmiany strumienia magnetycznego Φ_B przenikającego przez powierzchnię ograniczoną tym obwodem , czyli :
. Indukcja wzajemna. Jeżeli w jednym obwodzie zmienia się natężenie prądu to zgodnie z prawem indukcji Faradaya w drugim obwodzie znajdującym się w pobliżu pierwszego jest indukowana SEM. Zjawisko to jest nazywane indukcją wzajemną . SEM indukowana w drugim obwodzie wyniesie
. Samoindukcja(indukcja własna). Występuje w przypadku pojedynczego obwodu . Strumień magnetyczny wytwarzany przez prąd płynący w obwodzie przenika ten obwód, zatem każda zmiana natężenia prądu wywoła w nim powstanie SEM indukcji. Strumień magnetyczny Φ wytwarzany przez obwód i przenikający go proporcjonalny do natężenia prądu I płynącego w tym obwodzie Φ = LI , gdzie L nosi nazwę współczynnika indukcji własnej lub współczynnika samoindukcji. Indukowana SEM wynosi
.

ZESTAW D
Pęd (p) - wektorowa wielkość fizyczna charakteryzująca ruch postępowy ciała o kierunku i zwrocie pokrywającym się z kierunkiem i zwrotem wektora prędkości. Pęd ciała jest równy iloczynowi masy (m) i prędkości (V) poruszającego się ciała: p = mv.

Jednostką pędu jest kilogramometr na sekundę kg m/s - jest to pęd ciała o masie 1kg poruszającego się z prędkością 1m/s.

Popęd siły (impuls siły) - wektorowa wielkość fizyczna charakteryzująca działanie siły F na ciało w przeciągu czasu Δt; równa jest iloczynowi: FΔt.

Jednostką popędu jest niutonosekunda (Ns) - jest to popęd (impuls) siły udzielony ciału przez działanie na nie w czasie 1s stałej siły równej 1N.

Zasada zachowania pędu - w układach odosobnionych pęd całkowity układu, będący sumą wektorową pędów poszczególnych ciał układu, jest wielkością stałą. W układzie, na który nie działają niezrównoważone siły zewnętrzne, suma pędów początkowych p₀ oddziałujących na siebie ciał jest równa sumie pędów końcowych p_k tych ciał. Co zapisujemy w postaci p=const. lub p_k=p₀.

Moment pędu, kręt, wektor osiowy J charakteryzujący ruch ciała (w szczególności ruch obrotowy): J=r×p (iloczyn wektorowy wektora wodzącego r i pędu ciała).Dla układu ciał moment pędu układu jest sumą wektorową momentu pędu pojedynczych ciał, dla ciała o ciągłym rozkładzie masy moment pędu wyraża się wzorem:

Uogólnienie prawa Ampera

Liczne doświadczenia wykazały, że powyższe prawo jest również słuszne gdy mamy do czynienia nie tylko z prądem przewodzenia I płynącym przez przewodnik (który jest związany z ruchem przepływu ładunków elektrycznych np. elektronów), ale stosuje się również w przypadku prądu uogólnionego I_u. Prąd uogólniony I_u jest sumą prądu przewodzenia I i prądu przesunięcia I_p związanego ze zmianą w czasie natężenia pola elektrycznego (np. zmianą natężenia pola E w przestrzeni międzyelektrodowej kondensatora podczas jego ładowania lub rozładowywania). I_u = I + I_p

Liczne doświadczenia wykazały, że rzeczywiście między okładkami kondensatora powstaje pole magnetyczne (linie sił tego pola są okręgami, podobnie jak linie pola magnetycznego wokół przewodnika z prądem), przy czym pole to jest wytwarzane przez kondensator tylko wtedy, gdy się on rozładowuje lub ładuje, tzn. gdy zmienia się w czasie natężenie pola elektrycznego E kondensatora.

Wyrazimy obecnie natężenie prądu przesunięcia jako funkcję szybkości zmiany natężenia pola elektrycznego. Ładunek kondensatora zgodnie z wzorem wynosi: Q = εES. Różniczkując ten wzór względem czasu, otrzymujemy:
Oznaczając :
oraz wiedząc, że εdE•S = dΦ_D,S, możemy zapisać
Jak widzimy z wzoru powyżej prąd przesunięcia jest to po prostu szybkość zmian strumienia indukcji magnetycznej.

Korzystając z prądu uogólnionego , prawo Ampera możemy ostatecznie zapisać w postaci: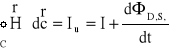
.

Równania Maxwella przedstawia się bądź w postaci całkowej, bądź w postaci różniczkowej. • uogólnione prawo indukcji elektromagnetycznej Faradaya,

• uogólnione prawo przepływu prądów Ampera ,• prawo Gaussa dla pola elektrycznego i

• prawo Gaussa dla pola magnetycznego .

Równania Maxwella stanowią fundamentalną podstawę teorii zjawisk elektromagnetycznych, podobnie jak zasady dynamiki Newtona są podstawą mechaniki.

Lp.	Równanie	Nazwa	Fakty doświadczalne
1		uogólnione prawo indukcji Faradaya	zmienne pole magnetyczne wytwarza wirowe pole elektryczne, które może wywołać prąd elektryczny
2		uogólnione prawo przepływu prądów Ampere 'a	prąd elektryczny lub zmienne pole elektryczne wytwarza wirowe pole magnetyczne
3		prawo Gaussa dla pola elektrycznego	ładunek wytwarza pole elektryczne o indukcji odwrotnie proporcjonalnej do kwadratu odległości
4		prawo Gaussa dla pola magnetycznego	nie istnieje w przyrodzie ładunek magnetyczny, linie indukcji sąkrzywymi zamkniętymi

Przepływ płynu. Ruch płynów nazywamy przepływem , a uporządkowany ruch cząsteczek płynów poruszających się w jednym kierunku strumieniem lub strugą . Przepływ nazywamy laminarnym, jeżeli strumień płynu może być rozłożony na warstwy , których wektor prędkości jest równoległy do kierunku przepływu. Przepływ płynu nazywamy turbulentnym , jeżeli zachodzi mieszanie się poszczególnych warstw płynu . W ruchu turbulentnym dla różnych warstw płynu pochodne prędkości względem czasu
. Jeżeli w danym punkcie przestrzeni prędkość przepływającego płynu nie zależy od czasu , to przepływ taki nazywamy ustalonym lub stacjonarnym.

Związek ten nosi nazwę równania ciągłości, z którego wynika , że prędkości cieczy w strudze są odwrotnie proporcjonalne do powierzchni przekrojów strugi.

. Równanie to nosi nazwę równania Bernoulliego. Dzieląc stronami powyższe równanie przez objętość V i podstawiając za m/V gęstość cieczy
otrzymamy postać równania następującą
. Na podstawie tych dwóch równań możemy sformułować prawo Bernouliego następująco : Suma energii kinetycznej, potencjalnej i ciśnienia jednostki masy (lub jednostki objętości) ustalonego przepływu cieczy doskonałej jest wielkością stałą.

ZESTAW E

Równoważność masy i energii E=mc² . E oznacza całkowitą energię ciała. Masa ciała w spoczynku jest równa masie i jego energia wynosi
i nazywamy ją energią spoczynkową, co oznacza że ciało będąc w spoczynku posiada pewną energię związaną z jego masą. Jeśli ciało to zostanie wprowadzone w ruch przez działanie siły. Praca tej siły zamieni się energię kinetyczną ciała . Energia kinetyczna ciała równa jest zatem różnicy energii całkowitej ciała w ruchu i jego energii spoczynkowej, czyli
po przekształceniu tego wzoru mamy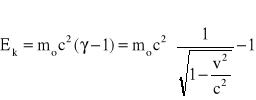
Wzór ten różni się w istocie od wzoru klasycznego
. Jednak można udowodnić że oba wzory dają te same wyniki dla niewielkich prędkości. W tym celu należy skorzystać z rozwinięcia w szereg :
w tym przypadku n = -1/2, a x = -v²/c². Zatem

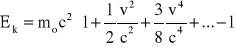
Jeżeli v <<c to w nawiasach możemy pominąć wyrazy o wyższych potęgach i otrzymamy
Otrzymaliśmy klasyczny wzór na energię kinetyczną , stanowiący szczególny przypadek wzoru relatywistycznego, gdy v <<c.

Według mechaniki relatywistycznej energia kinetyczna jest związana z przyrostem masy ciała. To samo dotyczy innych rodzajów energii. Na przykład każde ciało w miarę podnoszenia go nad poziom Ziemi, zwiększa swoją masę. Oczywiście zmiany te są tak niewielkie, że są niewykrywalne; dopiero w zjawiskach atomowych i jądrowych zmiana masy z energią są znaczne.

Temperatura jest wielkością skalarną określającą stopień nagrzania ciała. Jej równość zapewnia równowagę termiczną ciał będących w kontakcie (równowaga termiczna). Jednostką temperatury w skali bezwzględnej jest kelwin (K), a w skali Celsjusza stopień (^oC).

T-temperatura w skali bezwzględnej, t-w stali Celsjusza , a więc T = t + 273,15 .

Ciepłem nazywamy ilość energii wewnętrznej jaka przepływa między ciałami w wyniku różnicy temperatur. Ciepło jest mikroskopowym sposobem przekazywania energi. Jednostką ciepła podobnie jak energii i pracy jest dżul (J).

Ciepłem właściwym nazywamy ilość ciepła, jaką musi wymienić z otoczeniem ciało o masie 1 kg, aby jego temperatura zmieniła się o 1k.
, gdzie Q - ilość pobranego ciepła, m - masa, ΔT - przyrost temperatury , jednostką ciepła właściwego jest J/(kgK) .

Ciepłem molowym substancji nazywamy ilość ciepła potrzebną do ogrzania 1 mola tej substancji o 1K.
Q - ilość ciepła, n - liczba moli substancji , ΔT - zmiana temperatury, C - ciepło molowe. Jednostka ciepła molowego w układzie SI jest J/(mol K). Pomiędzy ciepłem właściwym a ciepłem molowym zachodzi związek C = cμ , gdzie μ - masa molowa.

Równanie stanu gazu doskonałego. Stan pewnej stałej ilości gazu określają jednoznacznie trzy parametry stanu : ciśnienie p , objętość V i temperatura T. PV = nRT, gdzie n - liczba moli danego gazu , a R = 8,314 J/(molK) - uniwersalna stała gazowa. Fikcyjny gaz , który dokładnie spełniałby to równanie w każdych warunkach, nazywamy gazem doskonałym.

Gazy rzeczywiste mają właściwości zbliżone do gazu doskonałego jedynie wtedy, gdy są rozrzedzone. Założenia wprowadzone dla gazu doskonałego przestają jednak obowiązywać przy dużych gęstościach gazu. Wtedy należy uwzględnić np. efekty związane z siłami spójności i skończoną objętość cząsteczek gazu. Zmodyfikowane równanie stanu gazów rzeczywistych dokładniej niż równanie Clapeyrona, zostało wprowadzone przez van der Waalas. Równanie van der Waalsa opisuje z dobrym przybliżeniem stan gazu rzeczywistego i ma postać :
, gdzie a i b - wielkości wyznaczone doświadczalnie dla danego gazu, v = V/n - objętość molowa
Prąd w cieczach ,mechanizm przewodzenia, elektroliza. Elektrolity

Czyste ciecze (z wyjątkiem roztopionych metali) są. złymi przewodnikami prądu elektrycznego. Stają się one dobrymi przewodnikami po rozpuszczeniu w nich kwasów, zasad i soli. Takie roztwory nazywamy elektrolitami. Elektrolity są to roztwory (przede wszystkim wodne) kwasów, zasad i soli.

W wyniku przepływu prądu elektrycznego przez, elektrolity na elektrodzie ujemnej -katodzie - wydzielają się takie substancje jak wodór, metale oraz grupy takie jak NH₄. Na elektrodzie dodatniej - anodzie - wydzielają się: tlen, reszty kwasowe oraz grupa OH. Wydzielanie się substancji w wyniku przepływał prądu przez elektrolit nazywamy elektrolizą.

Elektroliza

Przy przepływie prądu elektrycznego przez elektrolit na elektrodach woltametru (czyli naczynia, w którym odbywa się elektroliza) wydzielają się substancje chemiczne. Oznacza to, że w procesie elektrolizy transportowi ładunku towarzyszy transport masy. Z prawa zachowania ładunku wynika, że: do wydzielenia masy jednego mola dowolnego pierwiastka potrzebny jest przepływ ładunku Q_o.
gdzie: N _A = 6,02 •10²³ [l / mol] - to liczba Avogadra, w - wartościowość danego jonu, e - ładunek elementarny.

Prawo elektrolizy Faradaya

Pierwsze prawo Faradaya wyraża związek między ilością substancji wydzielającej się na elektrodzie, natężeniem prądu i czasem przepływu prądu przez, elektrolit. Prawo to ma następującą prostą treść: masa substancji m wydzielającej się na elektrodzie jest wprost proporcjonalna do należenia prądu I i do czasu jego przepływu t: m=kIt gdzie k oznacza współczynnik proporcjonalności, który zależy tylko od rodzaju wydzielającej się substancji i składu elektrolitu.

Drugie prawo Faradaya mówi, że współczynniki elektrochemiczne poszczególnych pierwiastków są wprost proporcjonalne do ich równoważników chemicznych.

Stąd wynika, że jeżeli w procesie elektrolizy, na elektrodzie wydziela się jeden gramorównoważnik substancji (tj. masa m równa liczbowo M/w) to przez elektrolit przepływa ładunek elektryczny Q liczbowo równy stałej F.

Innymi słowy stała Faradaya F równa się liczbowo ilości ładunku elektrycznego Q, który przepływając przez elektrolit, wydziela na elektrodzie jeden gramorównoważnik substancji.

ZESTAW E
Prawo Ampera i wzór Ampera

Obliczmy całkę krzywo liniową
po konturze zamkniętym C (w naszym przypadku po okręgu o promieniu r) wokół nieskończenie długiego prostoliniowego przewodnika z prądem. Ponieważ linie sił pola magnetycznego pochodzącego od prądu prostoliniowego tworzą w płaszczyźnie prostopadłej do przewodnika okręgi koncentryczne o środkach leżących na przewodniku. Indukcja
we wszystkich punktach okręgu jest taka sama i wynosi :
, a kierunek wektora
pokrywa się ze styczną do okręgu.

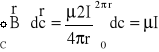
Wzór jest również prawdziwy dla konturu zamkniętego C dowolnego kształtu obejmującego przewodnik. Co więcej wynik całkowania jest taki sam, gdy przewodnik (nie jest prostoliniowy) ma dowolny kształt. Jeżeli kontur C nie obejmuje przewodnika z prądem, to cyrkulacja z wektora indukcji
po tym konturze jest równa zero.

Jeżeli kontur C obejmuje kilka przewodników z prądem to wobec zasady superpozycji pól magnetycznych wzór można zapisać: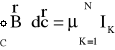
gdzie N- ilość przewodników z prądem obejmowanych przez kontur C . Wzór ten wyraża matematyczną postać prawa Ampera. Całka okrężna (po obwodzie zamkniętym) występująca w tym prawie nosi nazwę cyrkulacji albo krążenia wektora
.

Wiedząc, że
= μ.
możemy zapisać: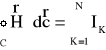
W tym przypadku prawo przepływu prądów tzw. prawo Ampera można sformułować następująco: Cyrkulacja wektora natężenia pola magnetycznego jest równa algebraicznej sumie natężeń prądów płynących wewnątrz konturu obejmującego te prądy.
Ciśnienie w cieczy i gazie . Prawo Pascala.

Ciecze i gazy noszą łączną nazwę płynów . Ciśnienie płynu można scharakteryzować wielkością siła działających na siebie poszczególnych warstw płynu lub na stykające się z nimi ciała . Stosunek siły parcia na dowolną powierzchnię w płynie do wielkości tej powierzchni nazywamy ciśnieniem . Jednostką ciśnienia jest paskal (Pa). Jest to ciśnienie jakie wywiera siła jednego niutona na powierzchnię 1 m² _--
Zjawisko to opisuje prawo Pascala, które można sformułować następująco: Ciśnienie zewnętrzne wywierane na ciecz lub gaz jest przenoszone we wszystkich kierunkach jednakowo.

p = p_o + δgh , gdzie δ gęstość cieczy, g - przyspieszenie ziemskie, h- głębokość mierzonego ciśnienia, p_o ciśnienie na powierzchni.

Prawo Archimedesa. Na ciało zanurzone w cieczy działa siła wyporu równa ciężarowi wypartej przez to ciało cieczy.

Pływanie ciał. Na każde ciało zanurzone w cieczy działa siła wyporu W = Vgδ_o i siła ciężkości Q = Vgδ - gdzie δ_o i δ oznaczają odpowiednio gęstość cieczy i średnią gęstość ciała niejednorodnego . Wypadkowa tych dwóch sił wyraża się wzorem R = W-Q = Vg(δ_o -δ).

Mogą tu wystąpić trzy przypadki: 1) δ>δ_o wówczas wypadkowa siła R<0 ciało będzie tonąć.

2) δ=δ_o - wówczas R=0 ciało będzie znajdować się w równowadze z cieczą na dowolnej głębokości zanurzenia, 3) δ<δ_o wówczas R>0 ciało będzie pływać częściowo zanurzone.

Czasoprzestrzeń, przestrzeń czterowymiarowa, w której oprócz trzech składowych przestrzennych występuje składowa czasowa, podstawowe pojęcie współczesnej fizyki, inaczej: przestrzeń zdarzeń fizycznych. Pojęcie czasoprzestrzeni wprowadził A. Einstein w szczególnej teorii względności.
Względności teoria szczególna, STW Podstawowe założenie STW to stałość prędkości światła w każdym układzie odniesienia (Michelsona-Morleya doświadczenie) - wynika z tego prawo transformacji współrzędnych przestrzennych i czasu przy przejściu od jednego układu odniesienia do drugiego, opisane przez transformację Lorentza, oraz postulat prawdziwości zasady względności głoszącej, że prawa fizyki mają taką samą postać w każdym inercyjnym układzie odniesienia.
Lorentza transformacja, Lorentza przekształcenie, przekształcenie matematyczne opisujące transformacje wielkości fizycznych w czasoprzestrzeni czterowymiarowej przy przechodzeniu od jednego inercjalnego układu odniesienia, określonego przez współrzędne przestrzenne x, y, z i współrzędną czasową t, do drugiego, określonego przez współrzędne x', y', z' oraz t'. W najprostszym przypadku, jeśli układ (x', y', z', t') porusza się jednostajnie w kierunku osi x z prędkością v, to transformacja Lorentza ma postać: gdzie c - prędkość światła w próżni.
transformacji Lorentza wynikają wszystkie efekty kinematyczne szczególnej teorii względności, takie jak: reguła sumowania się prędkości prowadząca do niemożności uzyskania prędkości większej od prędkości światła, względność pojęcia równoczesności, skrócenie Lorentza-Fitzgeralda, spowolnienie biegu poruszających się zegarów.
Nieinercjalny układ odniesienia, fizyczny układ odniesienia, w którym nie jest spełniona I zasada dynamiki Newtona: np. układ związany z obracającym się ciałem (w szczególności układ związany z Ziemią) lub ciałem poddanym przyspieszeniom liniowym. Przeciwieństwo układu odniesienia inercjalnego. W nieinercjalnym układzie odniesienia obserwuje się np. siłę Coriolisa, siłę odśrodkową, inne siły bezwładności.

---