<small><small></small></small><big><big>TEORIA ZAPA</big></big><small><small>SÓW</big></big><small><small>

</small></small>

<small><small></small></small><big>1. Logistyka - nauka o przepływie surowców i produktów gotowych, rodowód wojskowy.</big>

2. Utrzymanie zapasów jest związane z kosztem, występowanie braku w dostawie również powoduje koszty -> konieczność określenia optymalnej wielkości zapasów minimalizujących koszty.

3. Rozwiązanie najlepsze - systemy "just in time" (np. VOLVO)->bardzo duże wymagania na transport.

4. Podstawowe pytania TZ - jakiej wielkości partię towarów zamówić (wyprodukować) i w którym momencie.

5. Dwa podstawowe typy zadania TZ - kiedy zapotrzebowanie jest znane (problem deterministyczny), kiedy jest losowe (modele probabilistyczne).

6. Istnieje wiele metod otrzymywania decyzji optymalnych na podstawie stworzonych modeli np. programowanie całkowitoliczbowe, programowanie dynamiczne i inne.

Model 1:

Model ekonomicznej wielkości partii bez niedoborów:

Założenia:

 Zapasy są wykorzystywane w sposób ciągły, ze stałą intensywnością a sztuk w jednostce czasu.

• W momencie, gdy poziom zapasów osiąga 0 zamawiana jest partia towarów o stałej wielkości Q, która jest natychmiast dostarczana.

• Koszt zakupu jednej sztuki towaru wynosi c.

• Zawsze, gdy zamawiana jest partia towaru występuje stały koszt zakupu K.

• Koszt magazynowania jednej sztuki towaru przez jednostkę czasu wynosi h.

</div>

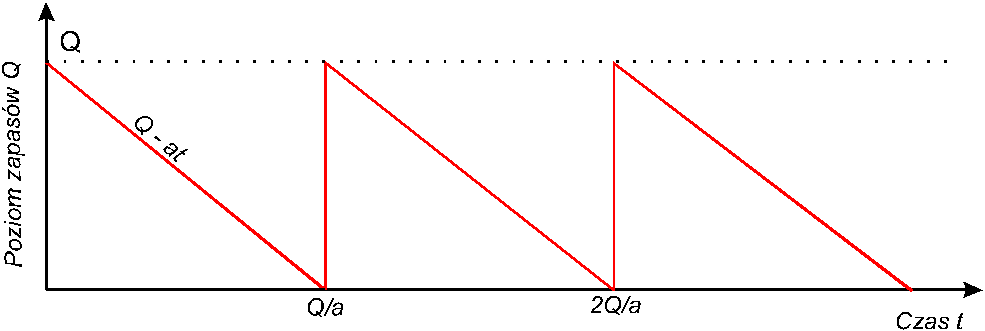
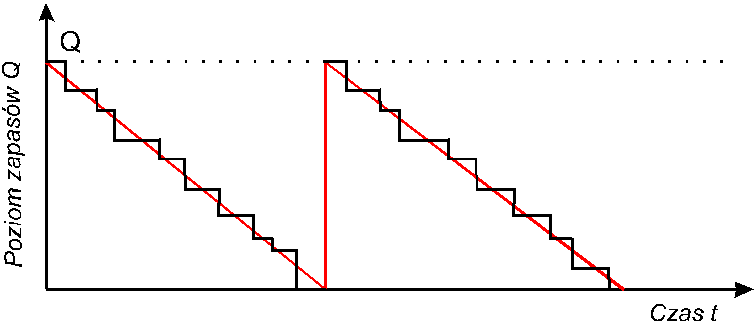
Zmiany poziomu zapasów w czasie. Aproksymacja liniowa

• Stałe zużycie.

• Cykliczne dostawy.

• Braki - niedopuszczalne.

Obliczenie kosztu całkowitego:

Koszt całkowity = koszt stały + koszt zakupu + koszt magazynowania

Koszt całkowity =

Obliczenie kosztu magazynowania:

Średni poziom zapasów w okresie [0,Q/a]

(Q + 0) / 2 = Q / 2

Średni koszt magazynowania w tym okresie

hQ / 2

Ponieważ długość cyklu wynosi Q / a zatem całkowity koszt magazynowania:

Obliczenie optymalnej wartości Q:

Koszt całkowity na jednostkę czasu:

Należy znaleźć punkt, w którym pochodna T(Q) równa sie zeru.

Zatem:

</div>

Zadanie 1a:

Firma przewozowa zużywa olej samochodowy w ilości 100l miesięcznie. Cena oleju wynosi 20 tys. zł. za litr. Każde złożone zamówienie wiąże się ze stałym kosztem 1 mln. zł. Olej musi być magazynowany w specjalnym budynku. Koszt magazynowania jednego litra oleju wynosi 5 tys. zł. miesięcznie. Zakładając, że nie są dopuszczalne braki określić optymalną wielkość zamawianej partii oleju, oraz minimalny miesięczny koszt całkowity.

 Rozwiązanie:

a = 100 l /mies.

c = 20 tys. zł. / l

K = 1000 tys. zł.

h = 5 tys. zł. / l /mies.   

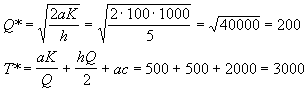
</div>

 Model 2::

 Model ekonomicznej wielkości partii z niedoborami:

Założenia:

 Zapasy są wykorzystywane w sposób ciągły, ze stałą intensywnością a sztuk w jednostce czasu.

• W momencie , gdy poziom zapasów osiąga 0 zamawiana jest partia towarów o stałej wielkości Q która jest natychmiast dostarczana.

• Koszt zakupu jednej sztuki towaru wynosi c.

• Zawsze, gdy zamawiana jest partia towaru występuje stały koszt zakupu K.

• Koszt magazynowania jednej sztuki towaru przez jednostkę czasu wynosi h.

Dla każdego okresu dopuszczalna jest stała wartość niedoboru. Występuje wówczas koszt karny p, za każdą jednostkę niezaspokojonego zapotrzebowania w jednostce czasu. </div><div align="center">

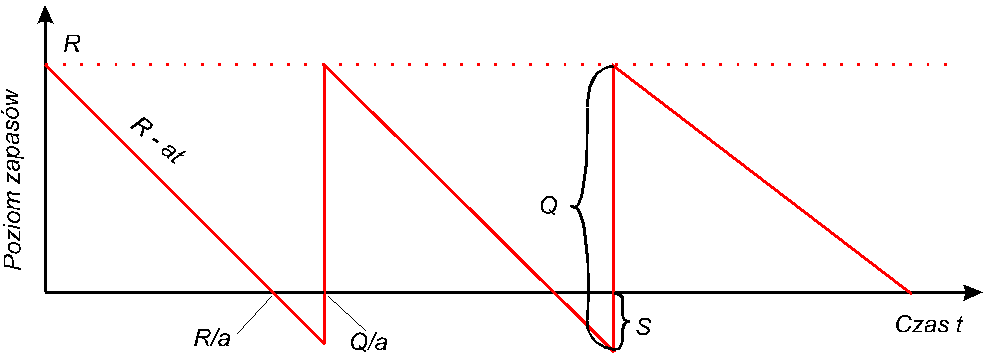
</div>S = Q - R  dopuszczalny poziom niedoborów;

R  początkowy poziom zapasów.

• Stałe zużycie,

• Cykliczne dostawy,

• Dopuszczalne niedobory.

 Obliczenie kosztu całkowitego:

Koszt całkowity= koszt stały + koszt zakupu + koszt magazynowania + koszt karny

Koszt całkowity =

Koszt całkowity na jednostkę czasu:

Obliczenie optymalnych wartości Q ,R:

Należy rozwiązać zadanie: min T(Q,R) Q > R

Należy znaleźć punkty zerowania się pochodnych: oraz

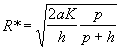
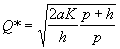
Otrzymujemy:

Zadanie 1b:

 Firma przewozowa zużywa olej samochodowy w ilości 100l miesięcznie. Cena oleju wynosi 20 tys. zł. za litr Każde złożone zamówienie wiąże się ze stałym kosztem 1 mln. zł. Olej musi być magazynowany w specjalnym budynku. Koszt magazynowania jednego litra oleju wynosi 5 tys. zł. miesięcznie. Jeżeli wystąpi niedobór oleju samochody muszą jeździć na oleju zużytym. Powoduje to koszt oceniany na ok. 50 tys. zł. za litr miesięcznie. Określić optymalną wielkość partii oraz długość przedziału, w którym samochody będą jeździły na zużytym oleju.

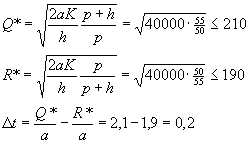
  Rozwiązanie:

a = 100 l / mies.

c = 20 tys. z3. / l

K = 1000 tys. zł.

h = 5 tys. zł. / l / mies.

p = 50 tys. zł. / l / mies.

 Model 3:

Model ekonomicznej wielkości partii z upustami cenowymi:

Założenia:

• Koszt zakupu jest uzależniony od wielkości partii tzn. stosowane są upusty cenowe.

• Niedobory są niedopuszczalne.

 

Jednostkowy koszt zakupu c=

c₁ > c₂ > c₃ > c₄

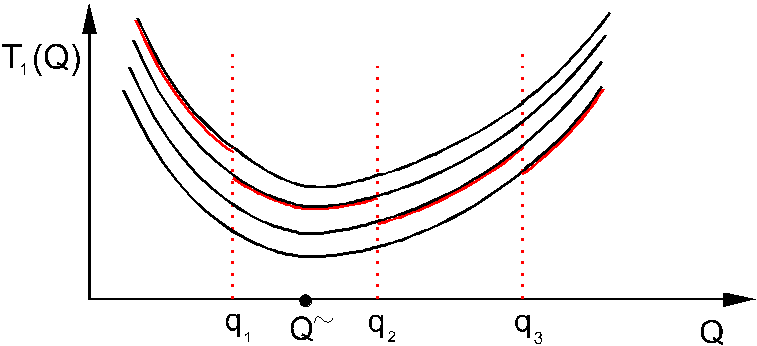
Obliczenie optymalnych wartości Q

Koszt całkowity na jednostkę czasu:

</div>Zadanie 1c:

Firma przewozowa zużywa olej samochodowy w ilości 100l miesięcznie. Cena oleju wynosi 20 tys. zł. za litr Każde złożone zamówienie wiąże sie ze stałym kosztem 1 mln. zł. Olej musi być magazynowany w specjalnym budynku. Koszt magazynowania jednego litra oleju wynosi 5 tys. zł. miesięcznie. Jeżeli zamówienie jest wieksze niż 300 l, cena wynosi 12 tys. zł. za litr. Jeśli zaś zamówienie jest wieksze niż 700 l to cena spada do 10 tys. zł. za litr. Obliczyć optymalną wielkość partii oleju oraz minimalny miesięczny koszt zakupu, przy założeniu że niedobory są niedopuszczalne.

Rozwiązanie:

a = 100 l /mies.

K = 1000 tys. zł.

h = 5 tys. zł. / l /mies.

c₁ = 20 tys. zł. / l jeoli Q < 300

c₂ = 12 tys. zł. / l jeoli 300 < Q < 700

c₃ = 10 tys. zł. / l jeoli Q > 700

 Model 4:

 Model z okresowymi przeglądami:

 Założenia:

 Zamówienia są składane na początku ustalonych przedziałów czasowych.

• Zapotrzebowanie jest różne w różnych okresach.

• Przedziały czasowe mogą być różnej długości.

• W każdym okresie zamówienie może być inne.

 Oznaczenia:

• Jest N przedziałów czasowych t = 1,2, ,N.

• D_t = zapotrzebowanie w przedziale t.
  Musi być zaspokojone na pocz1tku przedziału.

• x_t = wielkość zamówienia na początku przedziału t.

• I_t = wielkość zapasów na końcu przedziału t.

• c_t(x_t) = koszt zamówienia x_t sztuk towaru w przedziale t.

• h_t(I_t) = koszt magazynowania I_t sztuk towaru pobierany na końcu okresu t .

 D_t , x_t , I_t są całkowite.

 Sformułowanie problemu:

przy ograniczeniach:

I_t = I_t-1 + x_t - D_t

        x_t > 0 i całkowite   <big>  _} </big>dla t=1,2, .....,N

I_t > 0 i całkowite 

Programowanie całkowitoliczbowe nieliniowe

Sformułowanie problemu:

Na etapie n zdecyduj jaka ma być wielkość zamówienia na początku przedziału czasowego n, tzn. na etapie n określ x_n.

Na dowolnym etapie n , stan systemu s jest równy poziomowi zapasów na początku każdego przedziału n (przed zamówieniem).

Programowanie dynamiczne

 Określenie zależności rekurencyjnych:

 Danych jest N etapów.

• f_n(s , x_n) = koszt optymalnej strategii na etapy n , ,N , przy danym poziomie zapasów s na początku etapu n , oraz danej decyzji zamówienia x_n jednostek w etapie n.

• f_n(s) = koszt optymalnej strategii na etapy n , ,N przy danym poziomie zapasów s na początku etapu n.

 Poszukujemy f₁(I₀) , gdzie I₀ = początkowy poziom zapasów.

f_n(s,x_n ) = c_n(x_n) + h_n(s + x_n -D_n) +f_n+1(s + x_n - D_n)

f_n(s) = min { f_n(s , x_n)} , dla wszystkich x_n

<div align="center"></div>

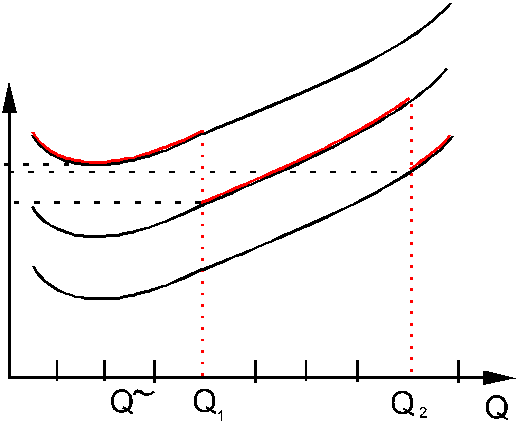
<big>Wklęsła funkcja kosztów:</big>

Strategia optymalna:

I_{t-1 } x_t = 0 dla wszystkich t

 Jeśli funkcje kosztów zakupu oraz kosztów magazynowania są wklęsłe, to strategia optymalna ma tę własność, że zamówienia występują jedynie wówczas, gdy poziom zapasów wynosi zero.

Dopuszczalne wartości x_n:

x_n = D_n lub D_n + D_n+1 lub  lub D_n + D_n+1 +  + D_N

Zadanie 2:

Jeden z wydziałów ZNTK dokonuje remontów generalnych silników lokomotyw elektrycznych. W trakcie remontu dokonuje się wymiany wirnika. ZNTK otrzymały następujące zamówienia na remont silników na najbliższe 5 tygodni: D₁ = 3 , D₂ = 4 , D₃ = 2 , D₄ = 5 , D₅ = 4.

Zamówienia te zostały już przyjęte i muszą zostać zrealizowane. ZNTK posiadają własny zakład, w którym produkowane są wirniki. Koszt uruchomienia produkcji serii wirników wynosi 20 mln. zł., zaś koszt wyprodukowania jednego wirnika wynosi 5 mln. zł. Koszt magazynowania wynosi 1 mln. zł. za każdy wirnik pozostały na koniec tygodnia. Jaka powinna być strategia produkcji wirników, aby zminimalizować koszt.

Rozwiązanie:

c_t(x_t) = 5x_t

h_t(I_t) = I_t

K = 20

I₀ = 0

c_t i h_t są funkcjami wklesłymi.

Określenie zależności rekurencyjnych:

f_n(s , x_n) = K + c_n(x_n) + h_n(I_n) + f_n+0(I_n)

f_n(s) = min {f_n(s , x_n) dla wszystkich x_n}

s = I_n-1

Poszukujemy f₁(0).

Korzystamy z zależności I_n-1 x_n = 0.

 ETAP 5:

Jeśli s = 0 to zamawiamy x₅ = D₅ = 4.

f₅(0) = 20 + 5  4 = 20 + 20 = 40.

x₅* = 4.

 ETAP 4:

Jeśli s = 0 to zamawiamy D₄ = 5 lub D₄ + D₅ = 9

f₄(0 , 5) = 20 + 5  5 + f₅(0) = 20 + 25 + 40 = 85

f₄(0 , 9) = 20 + 5  9 + 1  4 = 20 + 45 + 4 = 69

f₄(0) = 69.

x₄* = 9.

 ETAP 3:

Jeśli s = 0 to zamawiamy D₃ = 2 lub D₃ + D₄ = 7 , lub D₃ + D₄ + D₅ = 11.

f₃(0 , 2) = 20 + 5  2 + f₄(0) = 20 + 10 + 69 = 99.

f₃(0 , 7) = 20 + 5  7 +1  5 + f₅ (0) = 20 + 35 + 5 + 40 = 100.

f₃(0 , 11) = 20 + 5  11 + 1  (9 + 4) = 20 + 55 + 13 = 88.

f₃(0) = 88.

x₃* = 11.

 ETAP 2:

Jeśli s = 0 to zamawiamy D₂ = 4 lub D₂ + D₃ = 6 , lub D₂ + D₃ + D₄ = 11 lub

D₂ + D₃ + D₄ + D₅ = 15.

f₂(0 , 4) = 20 + 5  4 + f₃(0) = 20 + 20 + 88 = 128.

f₂(0 , 6) = 20 + 5  6 + 1  2 + f₄(0) = 20 + 30 + 2 + 69 =121

f₂(0 , 11) = 20 + 5  11 + 1  (7  5) + f₅(0) = 20 + 55 + 12 + 40 = 127.

f₂(0 , 15) = 20 + 5  15 + 1  (11 + 9 + 4) = 20 + 75 + 24 = 119.

f₂(0) = 119.

x₂* = 15

 ETAP 1:

Jeśli s = 0 to zamawiamy D₁ = 3 lub D₁ + D₂ = 7 , lub D₁ + D₂ + D₃ = 9 , lub

D₁ + D₂ + D₃ + D₄ = 14 , lub D₁ + D₂ + D₃ + D₄ + D₅ = 18.

f₁(0 , 3) = 20 + 5  3 + f₂(0) = 20 + 15 + 119 = 154.

f₁(0 , 7) =  ..........................

f₁(0 , 9) =  ..........................

f₁(0 , 14) =  ..........................

f₁(0 , 18) =  ..........................

f₁(0) =  ..........

.x₁* =  .....

.x₁ =  , x₂ =  , x₃ =  , x₄ =  , x₅ = 

Wypukła funkcja kosztów:

ALGORYTM:

Krok 1:

Zamów x₁ = D₁, tak aby zaspokoić zapotrzebowanie w etapie 1.

Krok 2:

Niech k będzie pierwszym przedziałem, w którym przynajmniej jedna jednostka zapotrzebowania jest niezaspokojona.

Rozważ możliwość zaspokojenia jednej jednostki zapotrzebowania, przez zamówienie jej w przedziale j,

gdzie j = 1 , 2  , k.

Krok 3:

Dla każdej z k możliwości oblicz przyrost kosztu. Wybierz możliwość o najniższym koszcie w możliwie jak najdalszym przedziale.

Krok 4:

Jeśli są przedziały o niezaspokojonym zapotrzebowaniu wykonaj „ Krok 2 ”. Jeśli nie, strategia jest optymalna.

 Zadanie 3:

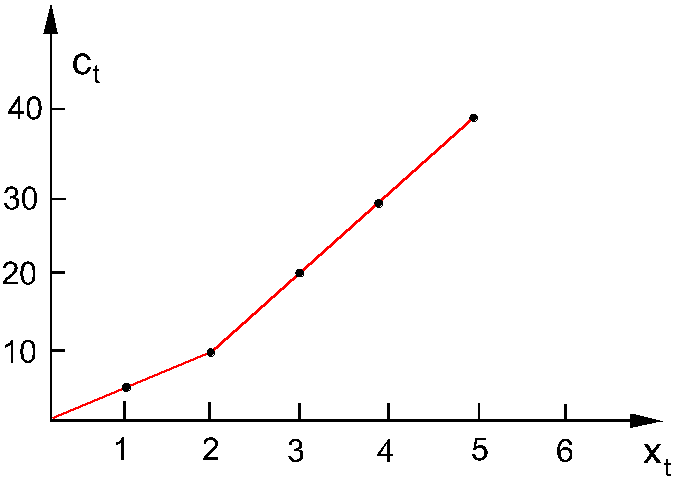
 Jeden z wydziałów ZNTK dokonuje remontów generalnych silników lokomotyw elektrycznych. W trakcie remontu dokonuje sie wymiany wirnika. ZNTK otrzymały nastepujące zamówienia na remont silników na najbliższe 3  y tygodnie: D1 = 4 , D2 = 1 , D3 = 3. Zamówienia te zostały już przyjete i muszą zostać zrealizowane. ZNTK posiadają własny zakład, w którym produkowane są wirniki. Może on wyprodukować co najwyżej 2 wirniki tygodniowo w cenie 5 mln. zł. ZNTK mogą zamówić wirniki w firmie prywatnej w cenie 10 mln. zł. Koszt magazynowania wynosi 3 mln. zł. za każdy wirnik pozostały na koniec tygodnia. Określić strategie produkcji (zamówien).

 Rozwiązanie:

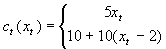
dla x_t  2

dla x_t >2

h_t(I_t) = 3I_t

</div>

Funkcje c_t i h_t są funkcjami wypukłymi

Krok 1:

x₁ = 4 , c₁(4) = 30

Krok 2: Krok 2: Krok 3:

k = 2 , j =1 , 2 k = 3 , j = 1 , 2 , 3  T1 = 16

Krok 3: Krok 3:  T2 = 8

T1 = 10 + 3 = 13  T1 = 16  T3 = 10

 T2 = 5  T2 = 8 X = (4 , 2 , 2)

X = (4 , 1 , 0)  T3 = 5

Krok 2: X = (4 , 1 , 2)

k = 3 , j = 1 , 2 , 3 Krok 2:

Krok 3: k = 3 , j = 1 , 2 , 3

 T1 = 10 + 2  3 = 16

 T2 = 5 + 3 = 8

 T3 = 5

X = (4 , 1 , 1) Strategia optymalna: x₁ = 4 , x₂ = 2 , x₃ = 2

Model 5:

 Jednoetapowy model probabilistyczny:

 Założenia:

*  Zapotrzebowanie D jest zmienną losową, która może przyjmować wartości ze zbioru R₊.

* Poziom zapasów na początku okresu wynosi zero.

 Oznaczenia:

x  poziom zapasów na początku etapu,

y  poziom zapasów po zamówieniu (y - x) sztuk towaru,

D  nieujemna zmienna losowa opisująca zapotrzebowanie,

f  funkcja gestości zmiennej losowej D,

F  dystrybuanta rozkładu zmiennej losowej D,

p  cena sprzedaży jednej sztuki towaru,

s  koszt niezaspokojenia jednostki zapotrzebowania,

c  koszt zamówienia jednej sztuki towaru,

h  koszt magazynowania jednej sztuki towaru, pobierany na koniec przedziału czasowego.

P  zysk uzyskany przy zamówieniu y sztuk towaru , x = 0.

Obliczenie zysku:

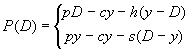
dla y>D

 dla yD

 

Definicja wartości oczekiwanej zmiennej losowej:

 x  zmienna losowa o funkcji gestości f

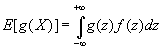
g  ciągła funkcja zmiennej losowej X

 E[P(D)] = p  E[D] - [cy + L(y)]

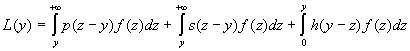
gdzie:

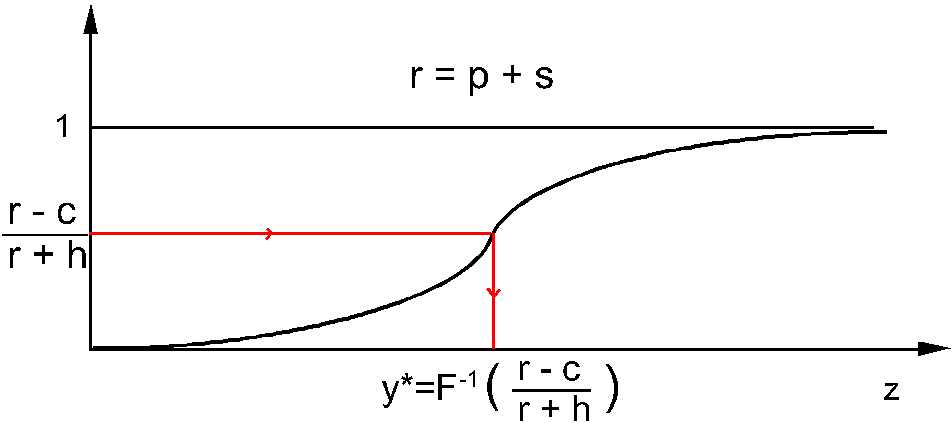
Obliczenie optymalnej wartości y:

 max E [P(D)] → min [cy + L(y)]

          

czyli   

</div>

 

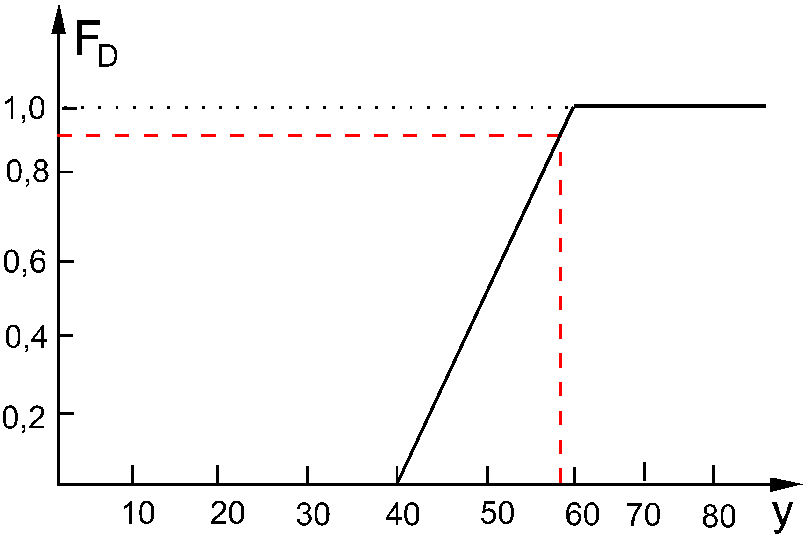
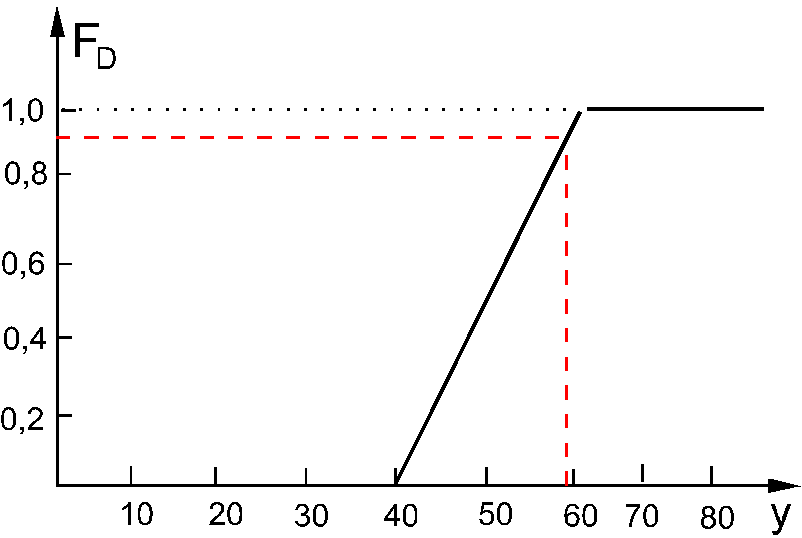
Zadanie 4a:

Zakłady WSK podpisały umowę z firmą AIRBUS na dostawę pewnego rodzaju części zamiennych. Dyrekcja WSK ocenia, że zapotrzebowanie na tę część ma rozkład równomierny w przedziale [40,60]. Wiadomo, że samolot bedzie wycofany z produkcji po upływie roku, zatem cała produkcja części ma być wykonana w chwili obecnej. Koszt produkcji wynosi $1000 za jedną część. Koszt sprzedaży natomiast wynosi $2000 za sztukę. Jeśli WSK nie będą miały dostatecznej liczby części zamiennych, to będą musiały zapłacić karę w wysokości $10000 za każdą  nie dostarczoną część. Koszty magazynowania wynoszą $100 za każdą część(obliczane są po upływie roku). Jaka liczba części powinna zostać wyprodukowana?

 Rozwiązanie:

 x = 0

p = 2000

s = 10000

c = 1000

h = 100

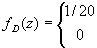
r = p + s = 12000

  z  60

w przeciwnym przypadku

 

 

Model 6:

 Jednoetapowy model probabilistyczny z początkowymi zapasami:

 Założenia:

• zapotrzebowanie D jest zmienną losową, która może przyjmować wartości ze zbioru R₊ .

• Poziom zapasów na początku wynosi x .

Obliczenie optymalnej wartości y:

Należy rozwiązać zadanie: Otrzymujemy:

min c(y - x) + L(y) dla y > x

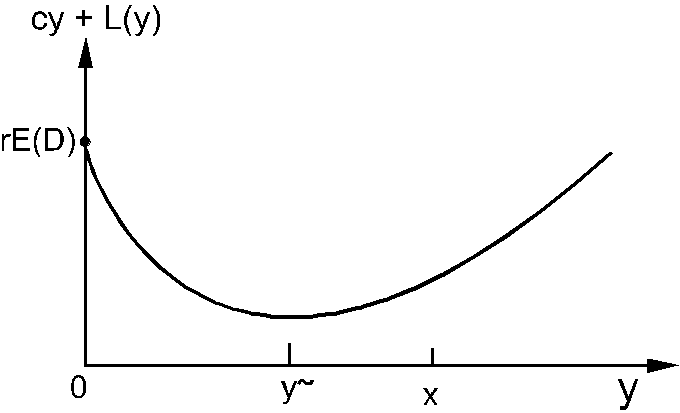
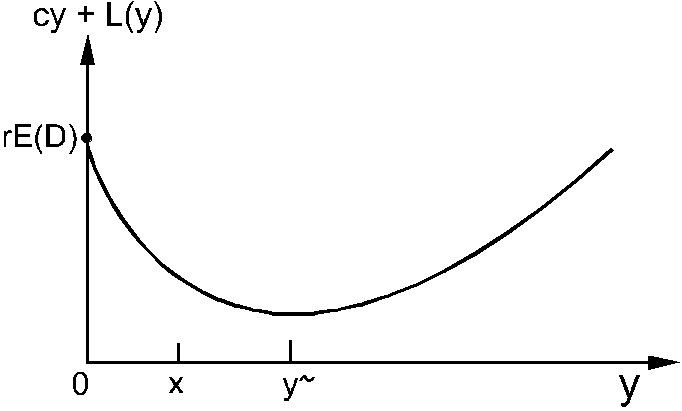
Decyzja optymalna:

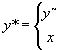
jeśli x  y~ zamawiaj y~ -x

jeśli x > y~ zamawiaj 0

Zadanie 4b:

 Rozwiązać zadanie 4a, przy nastepujących założeniach:

• Zakłady WSK poprzednio produkowały już części dla firmy AIRBUS i w magazynie znajduje sie jeszcze 25 szt. części.

• Jeśli po wycofaniu samolotu z produkcji w magazynach WSK pozostaną jeszcze niewykorzystane części zamienne, to AIRBUS odkupi je po $500 za sztukę.

Rozwiązanie:

x = 25

p = 2000

s = 10000

c = 1000

h = -500

r = p + s = 12000

</div>

 

 Model 7:

Jednoetapowy model probabilistyczny z początkowymi zapasami i kosztem stałym:

Założenia:

• Zapotrzebowanie D jest zmienną losową która może przyjmować wartości ze zbioru R₊

• Poziom zapasów na początku okresu wynosi x.

• Wystepuje stały koszt K związany z zamówieniem.

Obliczenie optymalnej wartooci y:

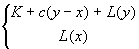
 Wartość oczekiwana kosztu =  Należy zbadać nierówność:

jeśli y > x

jeśli y = x

 

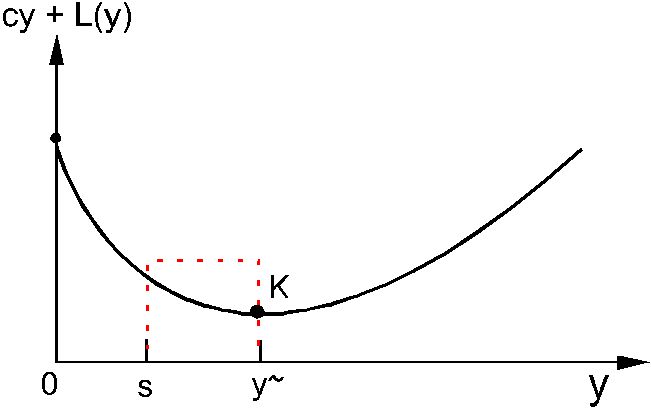
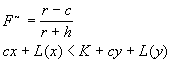
s  jest najmniejszą wartością dla której zachodzi:

cs + L(s) = K + cy^~ + L(y^~)

 

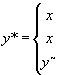
 Decyzja optymalna:

jeśli x > y^~ zamawiaj 0

jeśli s    x   y^~ zamawiaj 0

jeśli x < s zamawiaj y^~ - x

Zadanie 4c:

Rozwiązać zadanie 4b, przy nastepujących założeniach:

• Uruchomienie produkcji wiąże się ze stałym kosztem wynoszącym $20000.

Rozwiązanie:

x = 25

K = 20000

p = 2000

s' = 10000

c = 1000

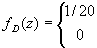
h = -500

40  z  60

w przeciwnym przypadku

Musimy znaleźć postać funkcji cy + L(y) oraz wartość y~

Nastepnie wartość s tak1 że zachodzi równość:

cs + L(s) = K + cy^~ + L(y^~)

r = p + s' = 12000

 

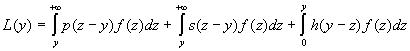
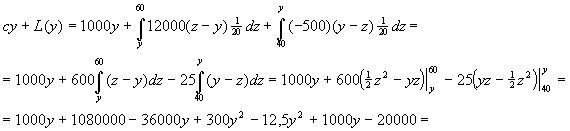
 Obliczenie y ^~:

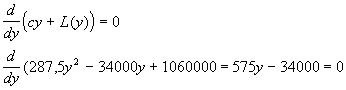
Obliczenie s':

K + cy ^~ + L(y ^~) = 74788

287,5s² - 34000s + 1060000 = 74788

287,5s² - 34000s + 1060000 = 0

s² - 118s + 3427 = 0

 = 118² - 4  3427 = 217

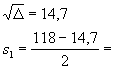
51,65

 

   

x < s

</div>

 Model 8:

 Dwuetapowy model probabilistyczny z początkowymi zapasami:

Założenia:

 Rozpatrujemy dwa etapy, w których zapotrzebowanie jest opisane tą samą zmienną losową.

• Nie wystepuje stały koszt związany z zamówieniem.

  D  nieujemna zmienna losowa opisująca zapotrzebowanie,

f  funkcja gestości zmiennej losowej D,

F  dystrybuanta rozkładu zmiennej losowej D,

p  cena sprzedaży jednej sztuki towaru,

s  koszt niezaspokojenia jednostki zapotrzebowania,

c  koszt zamówienia jednej sztuki towaru,

h  koszt magazynowania jednej sztuki towaru, pobierany na koniec przedziału czasowego.

x_n  poziom zapasów na początku okresu n = 1 , 2.

 Okreolenie zależnooci rekurencyjnych:

 ETAP  przedział czasowy,

STAN  poziom zapasów pozostały z poprzedniego etapu.

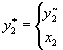
jeśli x₂ < y₂^~ zamawiaj y₂^~ - x₂

jeśli x₂  y₂^~ zamawiaj 0

 

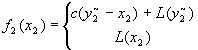
dla x₂ <

 dla x₂ >

 

Określenie decyzji optymalnej:

 f₁(x₁ , y₁) = c(y₁ - x₁) + L(y₁) + E[f₂(x₂)]

f₁(x₁) = min{f₁(x₁ , y₁) , dla y₁  x₁}

 Strategia decyzyjna:

 Na pocz1tku etapu 1:

jeśli x₁ < y₁^~ zamawiaj y₁^~ - x₁

w przeciwnym razie zamawiaj 0.

Na pocz1tku etapu 2:

jeoli x₂ < y₂^~ zamawiaj y₂^~ - x₂

w przeciwnym razie zamawiaj 0.

 Wklesła funkcja kosztów:

ALGORYTM:

1. Oblicz f_N(0) .

2. Mając dane f_N(0) , f_N-1(0) ,  , f_N+1(0) oblicz f_n(0) korzystając z faktu, że na etapie n należy uwzglednia decyzje x_n :
   x_n = D_n , D_n + D_n+1 ,  , D_n +  + D_N , a jedyny stan systemu jaki należy uwzglednia to
   s = 0.
   Dla każdej wartości x_n oblicz f_n(0 , x_n) .
   f_n(0) = min { f_n(0 , x_n) , x_n = D_n , D_n + D_n+1 ,  , D_n +  + D_N}.

3. Jeśli obliczyłeś f₁(0)  STOP. Jeśli nie wykonaj 2.

 

1

1

---