Nazwisko: BIRUNT Imię: WOJCIECH Kierunek: Fizyka z Informatyką II Rok studiów: 2000/2001r. Grupa laboratoryjna: XI		WYŻSZA SZKOŁA PEDAGOGICZNA w Rzeszowie I PRACOWNIA FIZYCZNA
				W y k o n a n o		O d d a n o
				Data 6.II.2001r.	Podpis	Data 13.II.2001r.	Podpis
Ćwiczenie nr 71	Temat: Sprawdzanie związku Lorentza - Lorentza dla roztworów

CZĘŚĆ TEORETYCZNA

Wektor polaryzacji dielektryka P definiujemy jako wypadkowy moment dipolowy na jednostkę objętości dielektryka

P=1/dV

n- liczba dipoli w jednostce objętości dielektryka

<Pe>- uśredniony po wszystkich dipolach moment dipolowy

Wektor polaryzacji P ma prosty związek z gęstością ładunku powierzchniowego δp w spolaryzowanym dielektryku .

Stała dielektryczna ∈ ośrodka izotropowego lub o symetrii układu regularnego zdefiniowana jest

∈=D/E=1+4π(P/E)=1+4πχ

χ=P/E- jest to podatność elektryczna.

5. makroskopowe uśrednione pole elektryczne

Polaryzowalność α atomu definiujemy : α=P/Elok

16. moment dipolowy atomu

Elok- lokalne pole elektryczne w miejscu w którym znajduje się atom

αjest zdefiniowane jako właściwość atomowa lub jonowa, χ oraz ∈ będą zależały również od sposobu w jaki atomy ułożone są w krysztale ponieważ E nie jest na ogół równe Elok.

Polaryzacja jest równa momentowi dipolowemu przypadającemu na jednostkę objętości

P=ΣNi*αi*Elok(i)

Ni- liczba atomów o polaryzowalności αi przypadająca na jednostkę objętości

Jeżeli pole lokalne związane jest z polem przyłożonym za pośrednictwem związku Lorentza.

Elok=E+4πP/3

P- lorentzowski współczynnik pola lokalnego

Wówczas otrzymujemy:

P/E=ΣNiαi / 1-(4π/3)ΣNiαi = (∈-1) / 4π

Możemy przedstawić w postaci:

(∈-1) / (∈+2) = 4π ΣNiαi / 3

Jest to związek Clausiusa - Mossottiego

PRZEBIEG ĆWICZENIA

Sporządzamy 8 roztworów (wody z cukrem) o stężeniach 0,5-10%. W tym celu posługujemy się wagą laboratoryjną. Po wykonaniu roztworów mierzymy kolejno współczynnik załamania światła w tych roztworach za pomocą refraktometru Abbego wykonując następujące czynności:

• przemywamy pryzmat czterochlorkiem wodoru

• nanosimy na niego kilka kropel badanego roztworu tak aby cała powierzchnia była pokryta cieczą

• lewym pokrętłem szukamy rozgraniczenia w postaci jasnej i ciemnej barwy

• prawym pokrętłem ustawiamy ostrość obrazu

• odczytujemy wskazania dla poszczególnych roztworów i zapisujemy w tabeli pomiarów

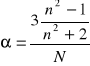
Obliczamy polaryzowatość α ze wzoru:

Obliczamy błędy pomiarów stężenia procentowego .

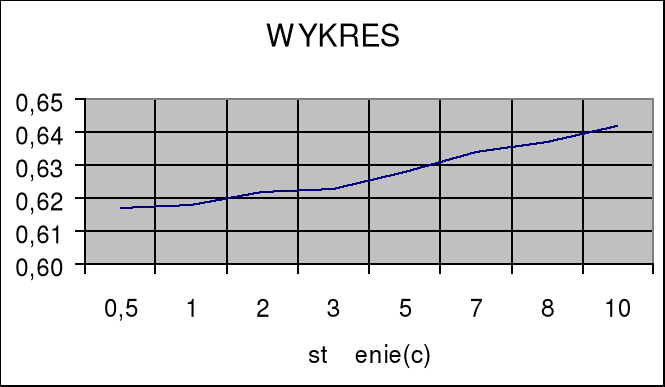
Sporządzamy wykres zależności ζ(c).

TABELA POMIARÓW

---