Nazwisko Nowak		WYŻSZA SZKOŁA PEDAGOGICZNA w Rzeszowie
Imię Tomasz		Wykonano		Oddano
Kierunek Fizyka z informatyką II		20-03-2001	Podpis	27-03-2001	Podpis
Grupa laboratoryjna: VIII
Nr ćwiczenia 71	Temat ćwiczenia Sprawdzanie związku Lorentza - Lorenza dla roztworów

Część teoretyczna

1. Pole elektryczne w dielektrykach.

Pole elektryczne jest to stan przestrzeni w otoczeniu elektrycznie naładowanego ciała, polegający na tym, że na umieszczony w niej nieruchomy ładunek elektryczny działa siła coulomba F_c. Pole elektryczne scharakteryzowane jest w dowolnym swym punkcie przez wektor natężenia pola elektrycznego E, zgodny co do kierunku i równy co do wartości bezwzględnej sile F, z jaką pole elektryczne działa na umieszczony w danym punkcie jednostkowy ładunek dodatni q_o:

E = F / q_o.

Zakłada się przy tym, że punktowy ładunek próbny q_o jest tak mały, że nie zakłóca pola elektrycznego, w którym jest umieszczony.

Dielektryk (izolator) jest to ciało nie przewodzące zauważalnego prądu elektrycznego, którego elektryczny opór właściwy jest większy niż 10⁸ Ω. Zatem dielektryk nie izoluje jednak zupełnie; tylko próżnia jest idealnym izolatorem. W dielektrykach nie występują swobodne ładunki elektryczne ; atomy i cząsteczki dielektryka są elektrycznie obojętne, gdyż dodatni ładunek jąder atomowych jest całkowicie skompensowany przez ujemny ładunek elektronów; elektrony te pozostają związane w danym atomie lub cząsteczce i nie mogą pod wpływem pola elektrycznego poruszać się swobodnie w całej objętości dielektryka.

Niemniej jednak doświadczenia wykazują, że dielektryk umieszczony w zewnętrznym polu elektrycznym modyfikuje to pole. Jeżeli np. weźmiemy kondensator płaski i przestrzeń między jego okładkami wypełnimy (izotropowym) dielektrykiem (np. olejem, szkłem, ebonitem)to pojemność kondensatora ulegnie zmianie, którą możemy opisać wyrażeniem:

C_d/C_o = ε

Gdzie:

C_d - pojemność kondensatora z dielektrykiem'

C_o - pojemność kondensatora próżniowego,

ε - przenikalność elektryczna danego dielektryka.

Wielkość ε jest większa zawsze od 1, więc pojemność kondensatora z dielektrykiem jest zawsze większa od pojemności tegoż kondensatora ale bez dielektryka. Zwiększenie to następuje (dla danego kondensatora, a więc dla takiej samej wartości S - powierzchni okładek i d - odległości między okładkami kondensatora) jedynie wskutek zmniejszenia się natężenia E między okładkami kondensatora. Zatem obecność dielektryka między okładkami kondensatora powoduje, że natężenie pola w tym obszarze zmniejsza się ε razy.

E = E_o / ε_o. E = E_o / ε.

Przyczyną tej modyfikacji jest polaryzacja dielektryka, polegająca na pewnym (mikroskopowym) przesunięciu ładunków elektrycznych w jego atomach i cząsteczkach, które częściowo kompensuje przyłożone do dielektryka pole zewnętrzne tak, ze natężenie pola wypadkowego staje się w nim mniejsze. Oznaczają natężenie dodatkowego pola elektrycznego wynikającego z polaryzacji przez E otrzymujemy zależność:

E = E_o + E'.

E = E_o - E'.

Podstawiając za E wcześniejsze wyrażenie E = E_o/ε i odpowiednio przekształcając otrzymane zależności otrzymamy:

E' = (ε - 1)E = χE E' = [(ε - 1)/ε]E_o.

Gdzie χ = ε - 1 oznacza podatność dielektryczną.

Na podstaw3ie powyższych wzorów otrzymujemy następującą właściwość dielektryków: natężenie dodatkowego pola elektrycznego E' wynikającego z polaryzacji dielektryka jest wprost proporcjonalne do natężenia pola zewnętrznego E_o oraz do natężenia pola wypadkowego.

Natężenie E_o wiąże się z gęstością powierzchniową ładunku δ na okładkach kondensatora wzorem

E_o = δ/ε_o.

Polaryzacja dielektryka prowadzi natomiast do pojawienia się na jego powierzchniach bocznych ładunków powierzchniowych (polaryzujących) o gęstości δ_p, ładunku ujemnego przy okładce naładowanej dodatnio i ładunku dodatniego przy okładce naładowanej ujemnie. Dodatkowe pole o natężeniu E' jest więc wytworzone przez dwie równoległe warstwy ładunków powierzchniowych o przeciwnych znakach i wartości gęstości δ_p, zatem:

E' = δ_p/ε_o.

Rozpisując wyrażenie na natężenie E otrzymamy:

E = E_o - E' = (δ/ε_o) - (δ_p/ε_o) = (δ - δ_p)/ε_o.

Gdzie:

E' = χE = δ_p/ε_o.

Zatem gęstość ładunków polaryzujących można wyrazić wzorem:

δ_p = ε_oχE.

Pojawienie się ładunków polaryzacyjnych dowodzi więc, że dielektryki składają się z atomów i cząsteczek, które mają wypadkowy ładunek elektryczny równy zero, nie jest to równoznaczne z tym, że nie mogą one wytworzyć pola elektrycznego. Zależnie od budowy dzielimy atomy i cząsteczki na polarne i nie polarne, przy czym podział ten jest oparty na wartości ich momentu dipolowego. Elektryczny moment dipolowy p jest określony jako wektor skierowany od ładunku ujemnego do dodatniego i opisany wzorem:

p = ∫ rρ(r)dv

gdzie

ρ(r) - gęstość ładunku w funkcji położenia.

Wartość bezwzględna elektrycznego momentu dipolowego p może być obliczona na podstawie zależności:

p = Q*l.

Ze względu na polarowość lub nie polarowość dielektryka, może on ulegać innemu rodzajowi polaryzacji. We wszystkich dielektrykach występuje polaryzacja indukowana (elektronowa i falowa), zaś w niektórych dielektrykach może występować dodatkowo polaryzacja orientacyjna.

Ilościowo polaryzację dielektryka opisujemy za pomocą wektora polaryzacji dielektrycznej P będącego sumą wektorową elektrycznych momentów dipolowych cząsteczek lub atomów znajdujących się w jednostce objętości.

P = (1/ΔV) Σ p_e = N < p_e > .

Gdzie:

N - liczba dipoli w jednostce objętości dielektryka,

< p_e > - uśredniony po wszystkich dipolach moment dipolowy.

Korzystając z powyższych definicji i dokonując odpowiednich przekształceń możemy otrzymać następujące zależności (dla rozważanego wcześniej kondensatora płaskiego):

P = p_e/ΔV = (δ_plΔS)/lΔS = δ_p = ε_oχE;

P = Np_e = Nαε_oE;

χ = Nα.

Gdzie α jest całkowitą polaryzowalnością.

Możemy również otrzymać związek pomiędzy wektorem polaryzacji dielektrycznej P a wektorem natężenia pola elektrycznego E postaci:

P = ε_oχE = ε_o(ε - 1)E.

Powyższe rozważania zachowują prawdziwość jedynie dla gazów rozrzedzonych, w których cząsteczki dielektryka znajdują się tak blisko siebie, że ich wzajemne oddziaływania można w pierwszym przybliżeniu pominąć. Dlatego w powyższych wzorach wektor natężenia pola E oznacz pole, które działa na cząsteczkę - jest ona pewnym polem uśrednionym w całym dielektryku, zwanym polem makroskopowym. Jednak, gdy rozważamy dielektryki o dużych gęstościach, musimy wówczas wprowadzić pojecie tzw. pola lokalnego E_lok. Ogólnie polem lokalnym E_lok nazywamy uśrednioną wartość pola działającego na wybraną, pojedynczą cząsteczkę. Jest ono równe:

E_lok = E_o + E + E_dod = E + E_dod.

Gdzie E_dod - pole działające na cząsteczkę, pochodzące od jej bliskich sąsiadów (tzw. polaryzacja otoczenia).

Obliczenie pola lokalnego w gęstym dielektryku przeprowadził po raz pierwszy włoski fizyk Ottoviano Mossotti w 1850 roku. Otrzymał on następujący wynik:

E_dod = P/(3ε_o) = [(ε - 1)/3] E;

E_lok = E + [P /(3ε_o)] = [(ε + 2)/3] E.

Pole działające na wybraną cząsteczkę w dielektryku nie polarnym, określone powyższym wyrażeniem nazywamy polem Mossottiego - Lorentza. A zatem wektor polaryzacji dielektrycznej P jest równy (dla dielektryków nie polarnych):

P = χε_oE_wł = Nαε_o[ E + P /(3ε_o)];

Stąd otrzymamy:

P = {Nα/[1 - (Nα)/3}ε_o E.

Podatność dielektryczna χ wyrażona jest więc wzorem:

χ = Nα/[1 - (Nα)/3].

Pisząc powyższą zależność dla dielektryka gazowego otrzymujemy:

χ_g = N_gα/[1 - (N_gα)/3] ≈N_gα; (N_gα)/3 → dąży do zera;

α = χ_g/N_g.

Natomiast dla cieczy (N_c - duże):

χ_c = N_cα/[1 - (N_cα)/3] = χ_g/[( N_g/N_c) - (χ_g/3)].

Jest tzw. wzór Mossottiego - Clauriusa (obowiązujący jedynie dla dielektryków nie polarnych).

Z ogólnego wzoru na podatność dielektryczną możemy uzyskać wyrażenie na polaryzowalność α:

α = [3*(χ/(3 + χ))]/N; χ = ε - 1.

α = [3*((ε - 1)/(ε + 2))]/N.

gdzie ilość cząsteczek N wyznaczyć możemy ze wzoru:

N = (N_Aρ)/M.

Gdzie:

N_A - liczba Avogadro,

M - masa molowa,

ρ - gęstość.

2. Dyspersja jest to zjawisko zależności współczynnika n załamania danej substancji od długości fali λ podającego światła. Gdy n maleje wraz ze wzrostem λ występuje wówczas zjawisko dyspersji normalnej, zaś gdy n rośnie wraz ze wzrostem λ wówczas występuje zjawisko dyspersji anomalnej.

W klasycznej teorii dyspersji światła, opracowanej przez L. Lorenza i H. A. Lorentza ośrodek jest traktowany jako zbiór oscylatorów harmonicznych o częstościach własnych ν_o, wykonujących pod wpływem padającego promieniowania drgania wymuszone. Amplituda tych drgań zależy od częstości światła ν. Gdy ν zbliża się do częstości własnej oscylatorów, tj. do wartości rezonansowej amplituda rośnie bardzo szybko - światło o tych częstościach jest przez ośrodek bardzo silnie absorbowane. Zależność współczynnika n od częstości ν padającego światła dana jest wzorem dyspersyjnym Lorentza - Lorenza:

[(n² - 1)/(n² + 2)] = DN Σ [F_i/(ν_oi² - ν)].

Gdzie:

D - stała dyspersji;

N - liczba cząsteczek w jednostce objętości;

F_i - siła oscylatora.

PRZEBIEG ĆWICZENIA

1. Sporządzić 8-10 roztworów cukru w wodzie o stężeniach od 0,5 do 10%.

2. Zmierzyć współczynnik załamania wody destylowanej za pomocą refraktometru Abbego.

Pomiar wykonać następująco:

-przemyć pryzmat refraktometru eterem lub czterochlorkiem węgla (CCl₄).

-za pomocą bagietki umieścić na powierzchni pomiarowej pryzmatu kilka

kropel wody tak, aby cała powierzchnia została pokryta cieczą.

Należy robić to ostrożnie, aby nie porysować pryzmatu.

• opuścić pryzmat pomiarowy

• otworzyć okienko oświetlające pryzmat (do oświetlenia można użyć lampki).

• obracając pokrętłem z lewej strony refraktometru znaleźć rozgraniczenie jasnego i ciemnego tła w górnym okienku okularu. Następnie za pomocą pokrętła z prawej strony refraktometru uzyskać ostre, bezbarwne rozgraniczenie jasnego i ciemnego tła w górnym okienku okularu. Linię rozgraniczenia naprowadzić na punkt przecięcia nici pajęczych

• w dolnym okienku okularu odczytać współczynnik załamania z dokładnością do 1/10 działki (w myśli podzielić ją na 10 części).

• pomiar powtórzyć 3 razy i znaleźć wartość średnią.

3. Posługując się refraktometrem Abbego jak w punkcie 2 zmierzyć współczynnik załamania światła dla poszczególnych roztworów cukru w wodzie.

4. Wyniki pomiarów umieścić w tabeli:

Lp.	Stężenie c (%)	Współczynnik załamania n

Wykreślić zależność ζ(c). Błąd pomiaru stężenia c można określić metodą pochodnej logarytmicznej, a błąd pomiaru ζ - metodą różniczki zupełnej.

5. Znaleźć polaryzowalność α wody:

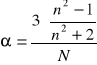
gdzie n jest zmierzonym wcześniej (pkt. 2) współczynnikiem załamania światła dla wody, a N można obliczyć ze wzoru:

gdzie N_A jest liczba Avogadro, ρ gęstością, a M masą molową.

Do obliczeń przyjąć:

N_A= 6,023 ^. 10²³mol ^-1

M= 18 ^. 10^-3 kg/mol

ρ=10³ kg/m³.

Błąd pomiaru α można obliczyć metodą różniczki zupełnej.

Tabela wyników pomiarów

Obliczenia:

Obliczam błąd stężenia metodą pochodnej logarytmicznej:

gdzie: m_s - masa substancji

m_r - masa roztworu

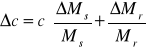
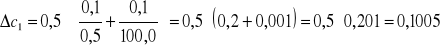
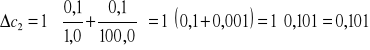
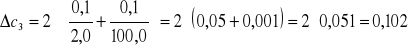
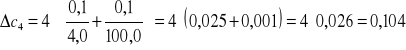
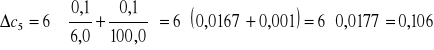
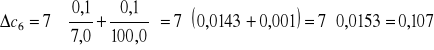
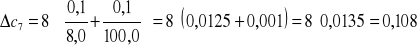
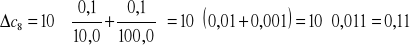
Obliczam polaryzowalność α dla wody ze wzoru:

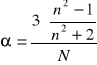
gdzie n jest współczynnikiem załamania światła dla wody, a N można obliczyć ze wzoru:

gdzie N_A jest liczba Avogadro, ρ gęstością, a M masą molową.

N_A= 6,023 ^. 10²³mol ^-1

M= 18 ^. 10^-3 kg/mol

ρ=10³ kg/m³

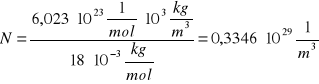
Dla wody współczynnik załamania światła: n=1,3323

Zatem :

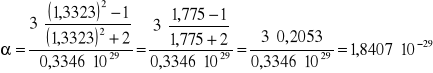
Błąd α obliczam metodą różniczki zupełnej. W związku z tym, że w mianowniku mamy stałą wartość błąd obliczam różniczkując licznik

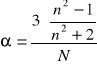
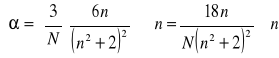
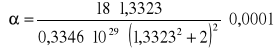
Obliczam ζ dla poszczególnych pomiarów:

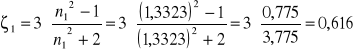
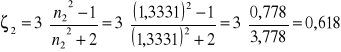
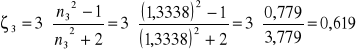
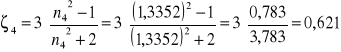
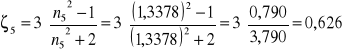
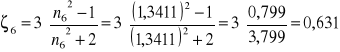
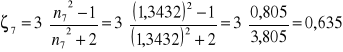
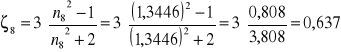
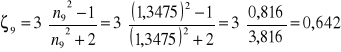
Wnioski:

Dołączony do sprawozdania wykres przedstawia zależność współczynnika Lorentza od stężenia roztworu ζ = ζ(c). Punkty pomiarowe są określone przez następujące wartości:

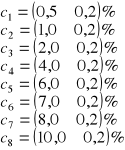
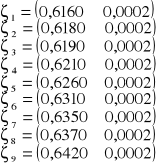
Pomiary wartości stężenia c oraz współczynnika ζ są obarczone niewielkimi błędami. Na błędy te decydujący wpływ miały dokładności użytych przyrządów. Tak więc na dokładność pomiaru stężenia roztworu decydujacy wpływ miała dokładność wagi, za pomocą której zostały wyznaczone masy cukru i wody. Natomiast na dokładność wyznaczenia współczynnika Lorentza decydujący wpływ miała dokładność refraktometru Abbego, a więc dokładność wyznaczenia wspólczynnika załamania. Można by również rozważać pewien wpływ niedoskonałości zmysłu widzenia (a dokładniej wrażliwości oka na różnice oświetlenia), jednak ze względu na bardzo małą wartość błędu można przyjąć dość wysoką precyzję odczytu.

Związek Lorentza - Lorentza został pomyślnie sprawdzony.

Druga część doświadczenia polegała na wyznaczeniu polaryzowalności wody. Otrzymano następujący wynik

Decydujący wpływ na pomiar tej wielkości z dokładnością δ(α) miała również dokładność wyznaczenia współczynnika załamania, a więc dokładność użytego refraktometru Abbego oraz ewentualnie niedoskonałość oka ludzkiego. Otrzymana wartość błędu jest jedna bardzo mała, co świadczy o poprawnym wyznaczeniu wartości α. Wielkość N określającą ilość cząsteczek wody w jednostce objętości uznajemu za wartość tablicową, nie obarczoną błędem.

---