Nazwisko BŁAZIK		WYŻSZA SZKOŁA PEDAGOGICZNA w Rzeszowie
Imię KATARZYNA		Wykonano		Oddano
Kierunek Fizyka z informatyką II		13-02-2001	Podpis	20-03-2001	Podpis
Grupa laboratoryjna: VIII
Nr ćwiczenia 78	Temat ćwiczenia Wyznaczanie długości fali rtęci za pomocą spektroskopu

Wstęp teoretyczny:

Wszystkie pomiary spektrofotometryczne polegają na zarejestrowaniu i ewentualnym zmie­rzeniu widma emitowanego, bądź absorbowanego, przez badaną próbkę materiału. Widmo emisyjne badamy w przypadku substancji, które pobudzone same emitują promieniowanie elektromagnetyczne. Widmo absorpcyjne badamy, przepuszczając przez badaną próbkę promieniowanie o widmie białym, tzn. o równej zawartości wszystkich harmonicznych. Po­przez obserwację zredukowanego widma, otrzymanego po przejściu światła przez próbkę, możemy określić jakie pierwiastki wchodzą w jej skład. Podstawy teoretyczne są następu­jące:

Pobudzony elektron schodzi na niższy poziom energetyczny emitując jednocześnie kwant energii w postaci fali elektromagnetycznej o odpowiedniej długości fali - tak powstaje widmo emisyjne;

Odwrotnie jest, gdy w przypadku dostarczenia elektronowi odpowiedniej porcji energii, pochłania on ją, wchodząc jednocześnie na wyższy poziom energetyczny. (pochło­nięte promieniowanie nie wydostaje się z próbki) - w tym przypadku mamy do czynienia z widmem absorpcyjnym.

Obserwację widm przy użyciu spektroskopu należało rozpocząć od skalowania przy­rządu. Polega to na odpowiednim usytuowaniu źródła światła, ustawieniu układu soczewek na ostre widzenie, a także odpowiednim ustawieniu układów nakładania skali. Skalowanie spektroskopu wykonujemy kierując na spektroskop światło emitowane przez próbkę helu, który przyjęto za wzorzec. Hel emituje falę elektromagnetyczną, która po analizie widmowej przedstawia się w postaci siedmiu barwnych prążków. Dwudziestocentymetrową skalę spektroskopu ustawiamy tak, żeby pierwszy prążek o barwie czerwonej (odpowiadający długości fali 706.52 nm) pokrywał się z kreską 0.0 skali. Pozostałe prążki o znanych długo­ściach fal pozwalają wyznaczyć, na podstawie centymetrowej skali, długości fal prążków innych badanych próbek. Spektroskop zasadniczo służy do analizy jakościowej widma, ponieważ pomiar natężenia światła w odpowiednim pasmie jest wysoce subiektywny, z uwagi na bardzo małą czułość oka ludzkiego na zmianę natężeń promieniowania widzial­nego. Z grubsza rzecz biorąc pozwala jednak na ocenę charakterystyki obserwowanego spektrum.

Do analizy ilościowej bardziej przydatny od spektroskopu jest spektrofotometr, w którym wszelkie dane otrzymujemy w postaci liczby wyznaczonej z dokładnością nawet 1%. Natężenie światła dla danej długości fali odczytujemy nastawiając pokrętło mikrometryczne spektrofotometru na tą długość i odczytując z miernika magnetoelektrycznego procentową przepuszczalność optyczną próbki. Skalowanie spektrofotometru polega na ustawieniu skrajnych wartości 0% i 100% dla próbki przezroczystej (tzn. o całkowitej przepuszczalno­ści optycznej).

Pomiary podzielono na dwie części: pomiary spektroskopem i spektrofotometrem. Badano głównie widmo absorpcyjne szklanych filtrów optycznych. Badanie filtrów za pomocą spektroskopu polegało na subiektywnym określeniu natężenia światła, w poszczególnych pasmach, po przejściu przez badaną próbkę i wyznaczeniem długości fali odpowiadającej danej wartości odczytanej ze skali. Ze względu na nieczułość oka ludzkiego na ultrafiolet i podczerwień niemożliwe było określenie przepuszczalności próbki dla odpowiadającym im zakresom długości fal. Wyniki otrzymane przy tych badaniach zestawione są w tabeli i na wykresach. Za pomocą spektroskopu badano dwa filtry - czerwony i niebieski.

Pomiary wykonane spektrofotometrem Spekol wykonano dla próbek czerwonej i zielonej. Nastawienia długości fali dokonano z dokładnością Δ=1nm, a odczyt przepuszczalności z dokładnością Δ=1%. Wyniki otrzymane podczas pomiarów zestawione są w tabeli oraz na wykresie.

PRZEBIEG ĆWICZENIA:

1. Wyładowanie w atmosferze par rtęci wywołujemy za pomocą transformatora wysokiego napięcia. Po uzyskaniu ostrego widma liniowego rtęci oświetlamy podziałkę skali.

2. Odczytujemy na skali położenia trzech żądanych linii spektralnych l₁, l₂, l₃ o długościach odpowiednio _, _, _ oraz położenie linii nieznanej l_x .

3. Stałe Hartmana wyliczamy z zależności:

Tabelka

barwa linii	liczba działek l		długość fali [nm]
czerwona	0	0
pomarańczowa	13	13	579,1
pomarańczowa	15	15	577,0
zielona	31	31	546,1
zielono-niebieska	71	71	491,6
fioletowo-niebieska	134	134	435,8
fioletowa	189	189	407,8

Obliczenia:

Stałą Hartmana l₀ obliczam z następującego wzoru:

błąd współczynnika l₀ obliczam metodą różniczki zupełnej ze wzoru:

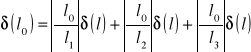
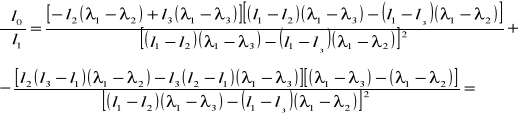
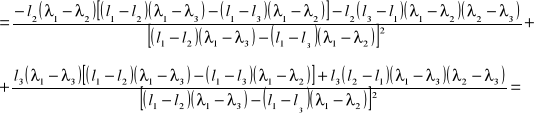
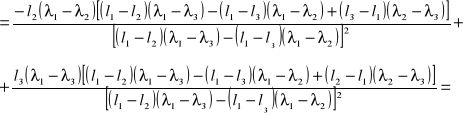
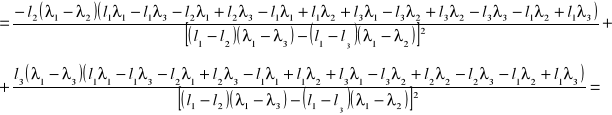
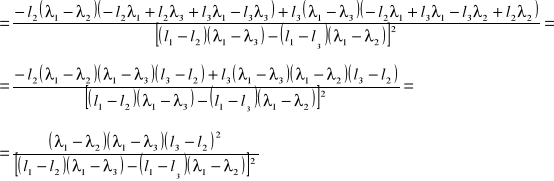
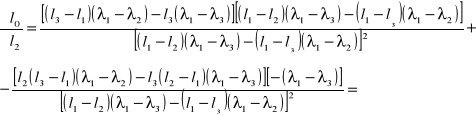
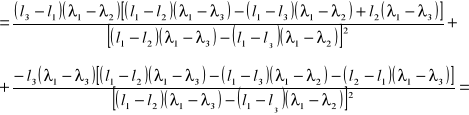
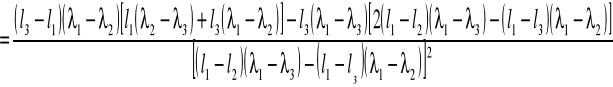
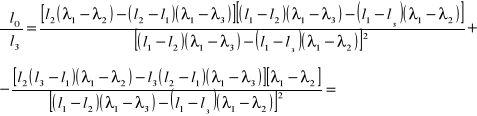
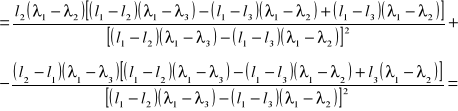
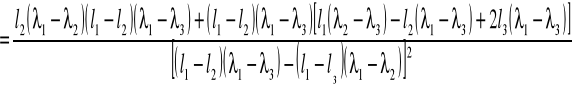
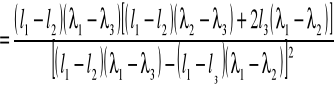
Stałą Hartmana c obliczam ze wzoru:

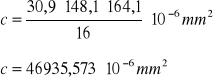
a błąd stałej c obliczam metodą różniczki zupełnej:

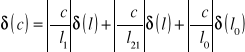
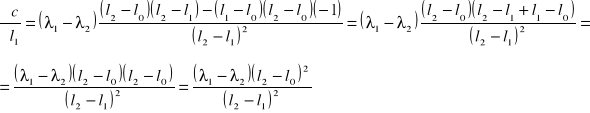
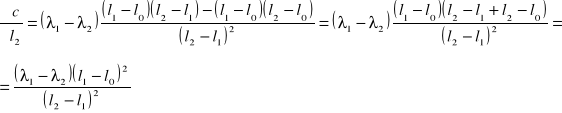
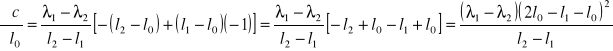
Stałą Hartmana λ₀ obliczam ze wzoru :
;

a jej błąd metodą różniczki zupełnej:

=

=

=

=

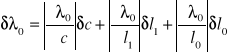
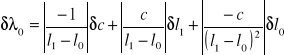
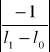
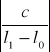
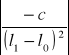
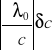
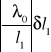
=0,21398939nm

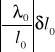
=28,888567nm

=33,371981nm

Długość nieznanej fali wyznaczam ze wzoru:
;

a jej błąd (podobnie jak poprzednio) obliczam metodą różniczki zupełnej:

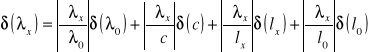
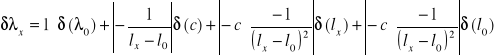
Wnioski:

Długość nieznanej fali jest obarczona błędem wynikającym z metody wyznaczania tej wielkości. Błąd ten zależy w szczególności od dokładności, z jaką wyznaczone zostały stałe Hrtmana, tzn. od wartości
, a także od dokładności odczytania położenia badanej linii na skali spektroskopu, a więc
.

Stałe Hartmana wyznaczone na podstawie położeń trzech znanych linii l₁, l₂, l₃ mają następujące wartości:

Na dokładność wyznaczenia każdej z tych stałych wpływ ma głównie dokładność odczytu położenia fali na skali spektroskopu. Tak więc na dokładność wyznaczenia długości badanej fali w ogólności wpływa tylko dokładność odczytu jej położenia δ(l). Jest ona stosunkowo duża (δ(l)=0,1mm) i błąd, jakim obarczony jest pomiar λ_x jest też stosunkowo duży (10,2%), co należy tłumaczyć skomplikowaną metodą wyznaczania tej wielkości (poprzez trzy stałe Hartmana). Dokładność wyznaczenia λ_x można by zwiększyć jedynie poprzez zwiększenie dokładności odczytu położenia na skali, jednak to, ze względu na niedoskonałość zmysłu wzrokowego obserwatora jest trudne do zrealizowania.

Długość fali otrzymana w wyniku naszego doświadczenia

jest zbliżona do wyniku tablicowego: λ=491,6nm

---