STATYSTYKA

6. Na czym polega różnica między badaniem pełnym a częściowym?

1. BADANIE PEŁNE (całkowite, wyczerpujące) - polega na tym, że informacje o badanych cechach statystycznych są gromadzone od wszystkich jednostek statystycznych wchodzących w skład zbiorowości statystycznej.

2. BADANIE CZĘŚCIOWE (niepełne, fragmentaryczne) - obejmuje wybrane jednostki zbiorowości statystycznej. Zbiorowości statystycznej nie można poddać badaniu pełnemu w takich sytuacjach,

jak:

- badany element ulega zniszczeniu (badanie pełne oznaczałoby w tej sytuacji zniszczenie wszystkich elementów),

- badanie pełne jest zbyt kosztowne (np. z uwagi na dużą populację generalną),

- badanie pełne jest zbyt czasochłonne (np. duża dynamika zmian badanego zjawiska wymaga podjęcia szybkich decyzji),

- badana zbiorowość jest nieskończenie duża (w praktyce za taką populację można też uznać bardzo liczne populacje, np. liczbę potencjalnych internautów - w tej sytuacji można mówić wyłącznie o badaniu częściowym).

14. Rodzaje skal pomiarowych zmiennych. Związek ze statystykami

Cechy ilościowe określa się jako zmienne. Dla potrzeb pomiaru cech stosuje się cztery rodzaje skal : nominalną , porządkową, interwałową i ilorazową .

Skala nominalna - skala stosująca wyłącznie opis słowny dla potrzeb identyfikacji jednostki. Np. kobieta i mężczyzna . Nie są możliwe działania arytmetyczne na danych opisanych na skali nominalnej.

Skala porządkowa - służąca do porządkowania danych. Na przykład ranking szkół wyższych z punktu widzenia ich atrakcyjności.

Skala interwałowa - skala mająca własności skali porządkowej, gdyż możliwe jest porządkowanie jednostek statystycznych opisanych w tej skali , a jednocześnie jest możliwe określenie interwału ( przedziału ) liczbowego, w którym zawierają się obserwacje.

Skala ilorazowa - skala ma cechy skali interwałowej, a ponadto iloraz ma tutaj określoną interpretację. Dane opisane w skali ilorazowej przyjmują zawsze wartości liczbowe, np. waga itp.

22. Pojęcie rozkładu zmiennej; typy rozkładów

Rozkład zmiennej losowej -określa z jakim prawdopodobieństwem zmienna losowa przyjmuje poszczególne wartości.

Rozkład zmiennej losowej moze byc

• dyskretny (jezeli zmienna losowa moze przyjmuje skonczenie wiele lub przeliczalnie wiele wartosci),

• ciagły,

• ani dyskretny ani ciagły (do tej klasy naleza np. mieszaniny rozkładów dyskretnych u ciagłych.

Po co rozkłady?

• niektóre wielkości losowe mają zbliżony rozkład

• pewne typowe rozkłady da się opisać odpowiednimi wzorami

• znajomość rozkładu zmiennej losowej pozwala na określenie prawdopodobieństwa wystąpienia jej wartości w dowolnym przedziale

• dla niektórych rozkładów teoretycznych opracowano różne metody statystyczne

• znajomość rozkładu cechy umożliwia stosowanie metod statystycznych

Często używane rozkłady

• rozkład Bernoulliego

• rozkład binormalny

• rozkład χ²

• rozkład dwumianowy

• rozkład geometryczny

• rozkład Gumbela

• rozkład hipergeometryczny

• rozkład jednostajny

• rozkład normalny (rozkład Gaussa)

• rozkład normalny wielowymiarowy

• rozkład Poissona

• rozkład prostokątny

• rozkład Studenta

• rozkład wykładniczy

• rozkłady Leviego

7. Scharakteryzować ogólnie podstawowe miary dyspersji

Dyspersja to inaczej rozrzut, najczęsciej o charakterze przypadkowym (statystycznym) wyników pomiaru jakiejś wielkości (np. wielkości fizycznej) bądź rozrzut cech jakiejś populacji (wzrost, waga człowieka).

Miary dyspersji:

ROZSTĘP - Różnica pomiędzy największą i najmniejszą wartością zmiennej. Zastosowanie - Wykorzystywany do przybliżonej, wstępnej oceny zmienności (dyspersji) badanego rozkładu Wzór :
R = X_max - X_min

gdzie : X_max jest największą, a X_min najmniejszą wartością zmiennej.

II. WARIANCJA - Jest ona średnią kwadratu odchyleń wartości zmiennej od wartości średniej. Znana jest także jako drugi moment centralny (m₂ ). Zawiera informacje o średnim odchyleniu zmiennej od wartości średniej. Zastosowanie - Wykorzystywana jako wskaźnik zmienności w szerokim zakresie sytuacji. Jest miarą szerokości rozkładu w pobliżu wartości średniej
. Jeśli wariancja jest mała, wówczas wyniki poszczególnych pomiarów leżą w pobliżu wartości średniej ( rozkład w kształcie wąskiego dzwonu ). Jeżeli jest ona duża, to wyniki są bardziej rozproszone wokół średniej ( rozkład przyjmuje kształt szerokiego dzwonu).

Wzór :

III. ODCHYLENIE STANDARDOWE - Dodatnia wartość pierwiastka kwadratowego z wariancji. Jest miarą średniego odchylenia wyników pomiaru od wartości średniej. Zastosowanie -Wykorzystywane jako standardowy wskaźnik zmienności

Wzór :

IV. KURTOZA - Wskaźnik informujący o tym, czy rozkład jest wysmukły (leptokurtyczny), czy spłaszczony (platokurtyczny). Dla rozkładu wysmukłego - g₂ > 0 , dla rozkładu spłaszczonego- g₂ < 0. Zastosowanie - Wykorzystywany do określenia stopnia koncentracji wartości zmiennej wokół średniej.

Wzór :

gdzie:
;

V. SKOŚNOŚĆ - Wskaźnik asymetrii rozkładu wokół średniej. Zawiera on informacje o możliwych różnicach pomiędzy dodatnimi i ujemnymi odchyleniami od wartości średniej. Zastosowanie -Powszechnie stosowany jest dla wykazania czy rozkład wyników jest symetryczny (normalny). W rozkładzie symetrycznym rozkład wyników testowania jest równomiernie rozłożony wokół średniej. Dla rozkładu symetrycznego (normalnego) wartość tego wskaźnika jest równa zeru (g₁ = 0). W rozkładzie asymetrycznym (skośnym) rozkład wyników wokół średniej nie jest równomierny. Dla rozkładu asymetrycznego lewostronnie (skośnego ujemnie) wartość wskaźnika jest mniejsza od zera ( g₁ < 0 ). W takim rozkładzie przewaga liczebności występuje wokół wysokich wartości zmiennej.
Dla rozkładu asymetrycznego prawostronnie (skośnego dodatnio) wartość wskaźnika jest większa od zera ( g₁ > 0). W takim rozkładzie przewaga liczebności występuje wokół niskich wartości zmiennej.

Wzór :

gdzie:
;

15. Krzywa Gaussa - jej prawidłowości

Rozkład normalny, zwany też rozkładem Gaussa lub krzywą dzwonową jest jednym z najważniejszych rozkładów prawdopodobieństwa. Odgrywa ważną rolę w statystycznym opisie zagadnień przyrodniczych, przemysłowych, medycznych, socjalnych itp. Krzywa Gaussa (rozkład normalny) opisuje większość zjawisk w przyrodzie. Krzywa ta przybliża rozkład częstości dla zestawu danych, mających określoną średnią arytmetyczną i odchylenie standardowe. Ogólny kształt krzywej Gaussa we wszystkich przypadkach jest podobny i przypomina kształt dzwonu.
Położenie środka diagramu na osi poziomej zależy od średniej arytmetycznej. Jeśli średnia jest mała, to diagram jest przesunięty w stronę początku osi, jeśli jest duża, to przesunięty jest w stronę końca osi.
Natomiast "szerokość" diagramu zależy od odchylenia standardowego. Jeśli odchylenie jest małe, to "szerokość" też jest mała (wyniki są zagęszczone wokół średniej), jeśli odchylenie jest duże, to "szerokość" też jest duża (wyniki są oddalone od średniej).

Wzór na krzywą Gaussa ma postać:
, gdzie e
2,72,

3,14, m - średnia arytmetyczna, s - odchylenie standardowe. Zakres zmiennej x zależy od konkretnego zestawu danych, w naszym przypadku 0 < x < 100.

7. W jakich sytuacjach obliczamy współczynnik korelacji rangowej Spearmana - omówić sposób wyznaczania?

Współczynnik korelacji rang Spearmana służy do opisu siły korelacji dwóch cech w przypadku gdy:

• cechy są mierzalne, a badana zbiorowość jest nieliczna,

• cechy mają charakter jakościowy i istnieje możliwość ich uporządkowania.

Współczynnik korelacji rang Spearmana stosuje się do analizy współzależności obiektów pod względem cechy dwuwymiarowej (X, Y). Zakładając, że badamy n obiektów opisanych za pomocą dwóch cech, należy te obiekty uporządkować ze względu na wartości każdej cechy oddzielnie (dla x_i - r_1i, a dla y_i - r_2i). Obiektom w każdym z uporządkowań przypisujemy liczbę określającą ich miejsce położenia (1,2,3,...,n). Numery te nazywa się rangami, a procedurę nadawania rang - rangowaniem.

Współczynnik korelacji Spearmana zależy wyłącznie od uporządkowania zaobserwowanych wartości. Może zatem być stosowany do dowolnych zmiennych, których wartości można uporządkować rosnąco, takich jak np. wykształcenie.. Współczynnik korelacji Spearmana oraz testy jego istotności mogą być stosowane przy dowolnym rozkładzie porównywanych zmiennych.

Wzór na współczynnik korelacji rang Spearmana jest następujący:

,

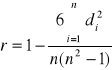
gdzie:

d_i = r_1i - r_2i,

r_1i - ranga i-tego obiektu w pierwszym uporządkowaniu,

r_2i - ranga i-tego obiektu w drugim uporządkowaniu,

n - liczba badanych obiektów.

Współczynnik korelacji rang Spearmana przyjmuje wartości z przedziału <-1,1>. Im bliższy jest on liczbie 1 lub -1, tym silniejsza jest analizowana zależność.

14. Na czym w statystyce polega zagadnienie pobierania prób? Rozkłady z prób

Próba to pewien podzbiór populacji generalnej, którego elementy zostały dobrane w sposób losowy bądź nielosowy. Innymi słowy: próba to „liczebność jednostek badania” Próba mała gdy
, gdy n>30 to mamy do czynienia z próbą dużą .

Wyróżnia się dwie procedury doboru próby :

1. Dobór celowy ( sprowadza się do tego , że o wyborze jednostek decyduje badacz, opierając się na merytorycznej znajomości problematyki badawczej, próba ta nie podlega prawu wielkich liczb )

2. Dobór losowy ( zgodny jest z zasadami doboru według metody reprezentacyjnej, umożliwia zastosowanie metod statystyki matematycznej do wnioskowania, próba ma charakter losowy, gdy każda jednostka populacji z jednakowym prawdopodobieństwem różnym od zera może się w niej znaleźć. Wyodrębniona próba podlega działaniu prawa wielkich liczb, co oznacza że wraz ze wzrostem liczebności próby losowej (n) rośnie stopień jej reprezentatywności )

Przed pobraniem próby ważne jest określenie jednostki losowania Indywidualna jednostka losowania pokrywa się z jednostką badania, a zespołową jednostką losowania , gdy nie pokrywa się z jednostką badania ( np. losuje się mieszkania a bada się ich osoby w nich zameldowane ).

---