4.2. Prawo Gaussa i przykłady jego zastosowań.

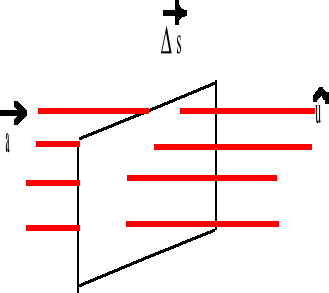
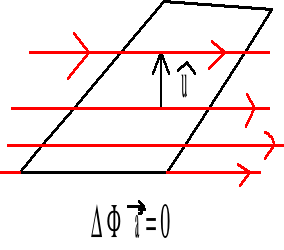
Strumień linii sił pola wektorowego o natężeniu
definiujemy następująco:

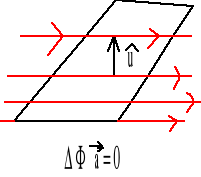
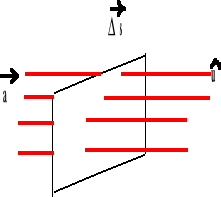
Można następująco sformułować prawo Gaussa dla pola grawitacyjnego:

Całkowity strumień pola grawitacyjnego przechodzący przez dowolna powierzchnię zamkniętą (tzw. powierzchnię Gaussa), jest proporcjonalny do masy będącej źródłem tego pola - tej, która jest zamknięta wewnątrz powierzchni Gaussa.

Zapisujemy to następująco:

gdzie
czyli ostatecznie

Przykłady zastosowania Prawa Gaussa do punktowego, liniowego i objętościowego rozkładu masy.

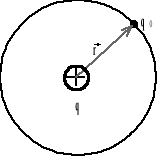
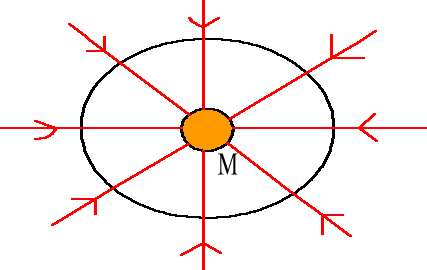
Strumień pola grawitacyjnego wytwarzanego przez źródło punktowe.

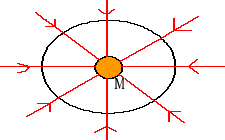
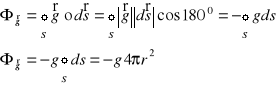
Uwaga! Znak „-„ związany jest z przeciwnym zwrotem wektorów
oraz
. Zgodnie z umową wektor
skierowany jest w stronę masy M.

Skoro:

a jak obliczono

więc stąd:

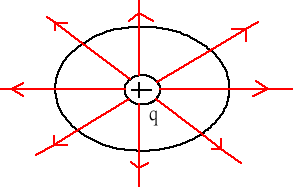
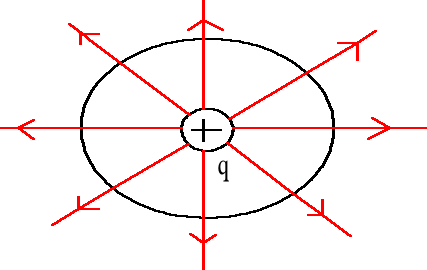
Stosując prawo Gaussa dla ładunku punktowego q > 0

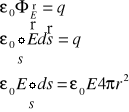
A więc
skąd:

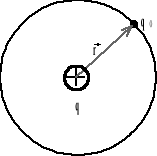
jeśli w odległości r od źródła q umieszczę ładunek punktowy q₀ to:

czyli

jest to siła Coulomba

Zastosowanie prawa Gaussa dla przestrzennego rozkładu masy.

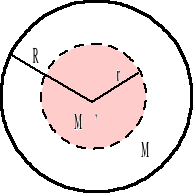
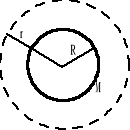
1. Sferyczny rozkład masy - powłoka kulista o masie M i promieniu R.

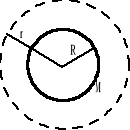
gęstość powierzchniowa masy:

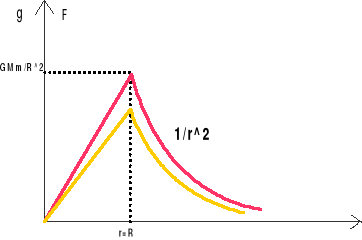
rozpatrujemy pierwszy obszar r > R

Na podstawie prawa Gaussa można zapisać:

gdzie M jest masą powłoki zawartej wewnątrz powierzchni Gaussa.

Uwaga na przeciwne zwroty wektorów
i
, gdyż ich iloczyn skalarny da wartość ujemną.

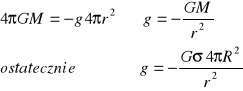
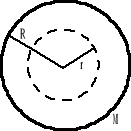
Dla drugiego obszaru r < R

gdyż żadna masa nie jest zawarta wewnątrz wybranej powierzchni Gaussa.

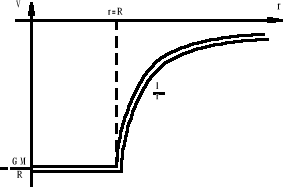
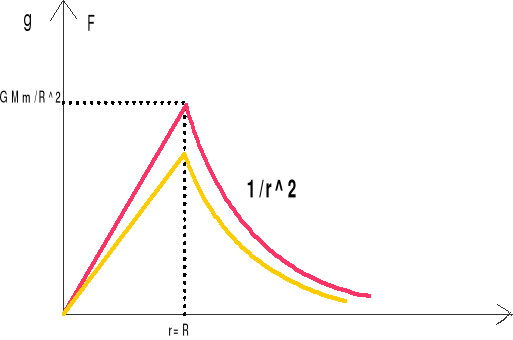
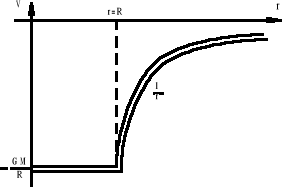
Zależność g(r) przedstawia poniższy wykres.

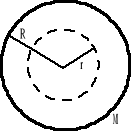
2. Objętościowy rozkład masy - kula o masie M, promieniu R i gęstości ρ.

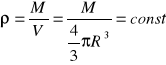
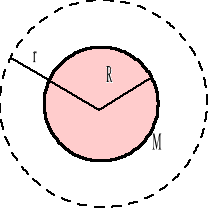
Rozpatrujemy pierwszy obszar r > R

(cała masa kuli zawarta jest wewnątrz

powierzchni Gaussa).

Można więc zapisać:

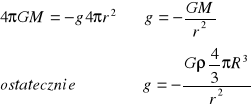
Można stąd obliczyć potencjał i energię potencjalną masy próbnej m znajdującej się w odległości r od źródła pola grawitacyjnego M.

Z kolei dla drugiego obszaru r < R tylko część masy kuli M' znajduje się wewnątrz wybranej powierzchni Gaussa

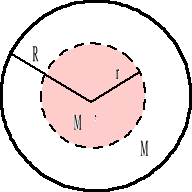
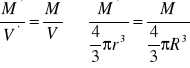
skąd

Na podstawie prawa Gaussa:

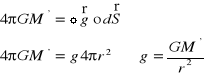
skąd ostatecznie:

Dla obu obszarów otrzymujemy ten sam wynik gdy r = R:

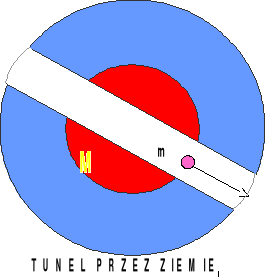
Przykład: tunel przez Ziemię.

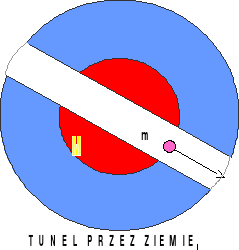
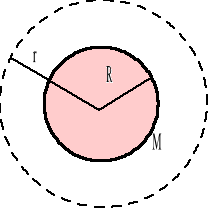
Powierzchnia Gaussa

r>R