Przekształcenie Fouriera. Różne postaci szeregu Fouriera. Przykłady i właściwości.
Szereg trygonometryczny Fouriera
Trygonometryczny szereg Fouriera dla przebiegów okresowych ma postać:
![]()
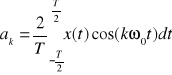
- współczynniki widma parzystego
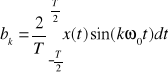
- współczynniki widma nieparzystego
Trygonometryczny szereg Fouriera jest równoważny wykładniczemu szeregowi Fouriera i zawsze postać wykładniczą można przekształcić do postaci trygonometrycznej i odwrotnie. Wynika to z faktu, że każdą liczbę zespoloną można przedstawić w postaci wykładniczej lub trygonometrycznej.
Amplituda i faza harmonicznej
![]()
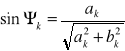
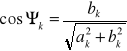
gdzie:
lub
![]()
gdzie:

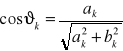
![]()
podstawiając za
otrzymamy inną postać szeregu trygonometrycznego Fouriera:
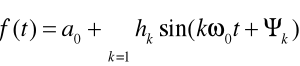
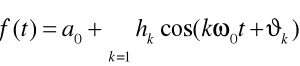
hk - amplituda k-tej harmonicznej, ၹk, ၊k - faza początkowa k-tej harmonicznej, ၷ0-pulsacja podstawowa
Widmo sygnału
Funkcja okresowa o okresie T rozłożona w szereg Fouriera zawiera składowe o częstotliwościach ၷ0, 2 ၷ0, 3 ၷ0...Wartości poszczególnych składowych są równe współ-czynnikom szeregu Fouriera. Układ współczynników odpowiadających poszczególnym częstotliwościom tworzy tzw. widmo częstotliwościowe. Istnieją więc dwa sposoby przedstawiania funkcji: w dziedzinie czasu i w dziedzinie częstotliwości.
Dla przedstawienia funkcji w dziedzinie częstotliwości potrzebne są dwa widma: widmo amplitudowe i widmo fazowe.
Widmo amplitudowe rzeczywistej funkcji okresowej jest symetryczne względem osi pionowej przechodzącej przez początek układu (jest to funkcja parzysta). Widmo fazowe jest funkcją symetryczną względem początku układu (funkcja nieparzysta).
Widmo amplitudowe i fazowe wyprostowanego sygnału sinusoidalnego
Szereg wykładniczy Fouriera
Warunki Dirichleta dla funkcji f(t):
funkcja f(t) musi posiadać skończone wartości maksimów i minimów w każdym skończonym przedziale
funkcja f(t) musi posiadać skończoną liczbę punktów nieciągłości w każdym skończonym przedziale
3. funkcja f(t) musi być bezwzględnie całkowalna
Dowolną, spełniającą warunki Dirichleta funkcję f(t) w przedziale (t0, t0+T) można przedstawić za pomocą sumy funkcji wykładniczych:
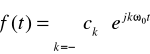
dla t0 < t < t0+T
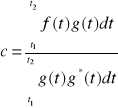
Na podstawie optymalnej wartości współczynnika c:
otrzymujemy szereg nazywany wykładniczym
szeregiem Fouriera
Współczynniki ck szeregu Fouriera przyjmują postać:
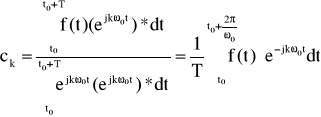
Współczynnik ck otrzymujemy poprzez aproksymację funkcji zespolonych w określonym przedziale. Współczynniki ck wyznaczone zostały z warunku minimalizacji błędu średniokwadratowego.
Szereg zespolony Fouriera
Wzory Eulera:
![]()
![]()
Postać zespolonego szeregu Fouriera:
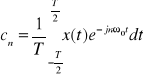
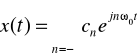
gdzie cn - amplituda zespolona
Ciąg An = ![]()
nazywamy widmem amplitudowym funkcji f(x).
Ciąg ၪn nazywamy widmem fazowym funkcji f(x):
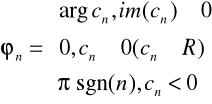
Transformacja Fouriera
Transformacja Fouriera jest podstawowym narzędziem analizy częstotliwościowej
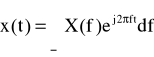
sygnałów. 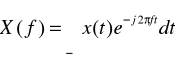
Prosta i odwrotna transformata Fouriera zdefiniowane są przez parę równań:
X(f) jest to zespolone widmo Fouriera sygnału, x(t) - zawiera informację o jego „zawartości częstotliwościowej”. Powstaje ono w wyniku wyznaczania miary korelacji (podobieństwa) sygnału do poszczególnych funkcji harmonicznych.
Ponieważ funkcje harmoniczne są zespolone, amplitudowe widmo Fouriera X(f) jest również zespolone:
![]()
![]()
W wyniku prostej transformacji Fouriera dokonujemy rozłożenia sygnału na jego składowe o różnych częstotliwościach. Z widma Fouriera sygnału można zsyntetyzować zdekompowany sygnał za pomocą odwrotnej transformacji Fouriera - należy wówczas zsumować (scałkować) wszystkie sygnały harmoniczne.
Sygnały okresowe o okresie T przedstawia się za pomocą szeregu Fouriera:
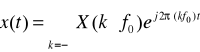
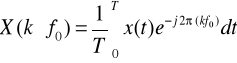
Właściwości transformacji Fouriera
Liniowość
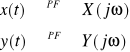
![]()
![]()
Przesunięcie w czasie
![]()
Przesunięcie w częstotliwości
![]()
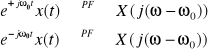
![]()
po dodaniu stronami:
![]()
Pomnożenie sygnału harmonicznego przez sygnał x(t) powoduje rozdzielenie widma na dwie części przemieszczone w lewo i prawo o wartość ၷ0. Operacja ta nazywana jest modulacją. Sygnałem modulowanym jest sygnał harmoniczny, a sygnałem modulującym sygnał x(t).
Odwrócenie w czasie
![]()
Skalowanie w czasie
![]()
Splot sygnałów
![]()
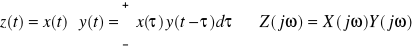
Iloczyn sygnałów
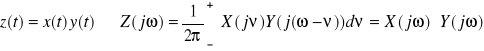
Zależność Parsevala
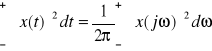
![]()
Bibliografia:
[1] http://gkrol.nex.com.pl/falki/
[2] http://imc.pcz.czest.pl/imtits/pliki_KUA/KUAcw4teoria.pdf
[3] http://www.kali.piasta.pl/naukaf/SEM7/semVIIfile/Elektrotechnika/wyklad/WeET7.pdf
[4] http://wms.mat.agh.edu.pl/~wojda/zbior/node17.html
[5] http://wms.mat.agh.edu.pl/~wojda/zbior/node18.html
[6] Mikołajuk K., Trzaska Z.: Elektrotechnika teoretyczna. Analiza i synteza elektrycznych obwodów liniowych, PWN, Warszawa 1984
[7] Musielak J.: Wstęp do analizy funkcjonalnej, PWN, Warszawa 1976
[8] Zieliński T.: Od teorii do cyfrowego przetwarzania sygnałów, WYDZIAŁ EAIiE AGH, Kraków 2002
![]()
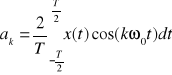
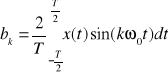
![]()
![]()
![]()
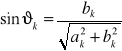
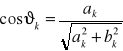
![]()
![]()
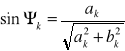
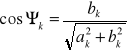
![]()
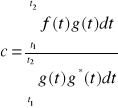
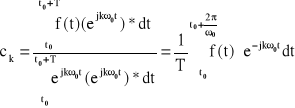
![]()
![]()
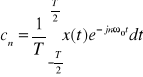
![]()
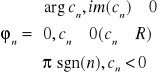
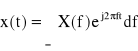
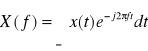
![]()
![]()
![]()
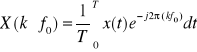
Wyszukiwarka
Podobne podstrony:
Fiz-amperomierz, woltomierz i ogniwo galwaniczne, Amperomierz włączamy do obwodu szeregowo, jego opó
Rezonans w obwodzie szeregowym(1), Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laborato
FOURIER, Automatyka i elektronika, Elektrotechnika - semestr 4
obwody prądów odkształconych Metoda Fouriera, ENERGETYKA I ELEKTRYKA
1Kompensacja szeregowa i rownolegla w liniach elektroenergetycznych, POLITECHNIKA POZNAŃSKA
Badanie silnika szeregowgo, Badanie silnika szeregowgo, Wydział Transportu ELEKTROTECHNIKA
PP praktyczne wykonanie szeregowej, rownoleglej sieci elektr
Elektrotechnika - Wstęp do wykładów, Akademia Morska, I semestr, elektro, Test wykład
wyklad 01 - bledy, MIERNICTWO ELEKTRONICZNE
WYKŁAD XIV, PWTRANSPORT, semIII, Elektrotechnika II
Spis wykladow, Polibuda, Semestr V, Kompatybilnosc Elektromagnetyczna, Wykład
Wyklad WdE3, Wstęp do elektrotechniki
Wykład 1 cd3 zagadnienie transportowe, Elektrotechnika-materiały do szkoły, Gospodarka Sowiński
Wyklad WdE2, Wstęp do elektrotechniki
Wyklad WdE4, Wstęp do elektrotechniki
Wyklad WdE5-b, Wstęp do elektrotechniki
więcej podobnych podstron