|
Wydział Elektroniki Politechniki Wrocławskiej
|
Laboratorium miernictwa |
||
Wykonał
|
Grupa
|
Ćw. nr
|
Prowadzący
|
|
Statystyczna analiza wyników pomiarów
|
Data wykonania
|
Data oddania
|
Ocena
|
|
CEL ĆWICZENIA
Celem ćwiczenia jest: uświadomienie studentom, że każdy wynik pomiaru obarczony jest błędem o nie zawsze znanej przyczynie i wartości, zapoznanie ze statystyczną analizą wyników pomiarów, sposobami znajdowania i eliminacji wyników obarczonych błędami grubymi, oceną składowej przypadkowej błędu, wskazanie na konieczność analizy warunków i wyników pomiarów pod kątem obecności składowej systematycznej błędu.
SPIS PRZYRZĄDÓW
Suwmiarka elektroniczna z wyświetlaczem LCD o parametrach metrologicznych:
- rozdzielczość 0,01mm,
- błąd graniczny 0,03mm
ANALIZA WYNIKÓW POMIARÓW
1. Tabele wyników dla trójkąta nr 5.
Tabela 1 Pomiary boków i wysokości trójkąta nr 5
Numer Studenta |
a [mm] |
b [mm] |
c [mm] |
ha [mm] |
hb [mm] |
hc [mm] |
1 |
92,24 |
84,43 |
75,41 |
65,37 |
|
79,69 |
2 |
92,14 |
84,40 |
75,40 |
65,16 |
71,23 |
79,61 |
3 |
92,15 |
|
75,40 |
65,18 |
71,25 |
|
4 |
92,17 |
84,35 |
75,40 |
65,19 |
71,24 |
79,63 |
5 |
92,11 |
84,40 |
75,42 |
65,18 |
71,25 |
79,69 |
6 |
91,93 |
84,33 |
75,33 |
65,08 |
71,23 |
79,68 |
7 |
91,87 |
84,29 |
75,37 |
65,11 |
71,22 |
79,62 |
9 |
92,07 |
84,37 |
75,40 |
65,07 |
71,23 |
79,69 |
11 |
|
|
|
65,23 |
71,24 |
79,59 |
12 |
92,04 |
84,27 |
75,40 |
65,12 |
71,21 |
79,65 |
13 |
92,31 |
84,32 |
75,50 |
|
71,24 |
79,63 |
14 |
92,19 |
84,41 |
75,40 |
65,30 |
71,22 |
79,69 |
15 |
92,08 |
84,38 |
75,38 |
64,97 |
71,22 |
79,64 |
16 |
92,21 |
84,42 |
75,42 |
65,19 |
71,24 |
79,71 |
17 |
92,31 |
84,32 |
75,50 |
|
71,24 |
79,63 |
18 |
92,38 |
84,45 |
|
65,34 |
71,23 |
79,67 |
19 |
92,11 |
84,40 |
75,42 |
65,18 |
71,25 |
79,69 |
20 |
92,14 |
84,40 |
75,40 |
65,16 |
71,23 |
79,61 |
21 |
92,14 |
84,40 |
75,40 |
65,16 |
71,23 |
79,61 |
|
92,091 |
84,391 |
75,301 |
64,982 |
71,237 |
79,660 |
S |
0,260 |
0,366 |
0,325 |
0,674 |
0,019 |
0,051 |
*a,b,c- boki trójkąta, ha , hb , hc - wysokości prostopadłe do odpowiednich boków.
Tabela 2 Obliczenia pól trójkąta nr 5
Numer Studenta |
Pa [mm2] |
Pb [mm2] |
Pc [mm2] |
PH [mm2] |
1 |
3014,86 |
3009,93 |
3004,71 |
2995,82 |
2 |
3001,92 |
3005,91 |
3001,30 |
2993,10 |
3 |
3003,17 |
3050,21 |
3009,21 |
3023,21 |
4 |
3004,28 |
3004,55 |
3002,05 |
2992,35 |
5 |
3001,86 |
3006,75 |
3005,11 |
2993,22 |
6 |
2991,40 |
3003,41 |
3001,15 |
2985,68 |
7 |
2990,83 |
3001,57 |
3000,48 |
2984,93 |
9 |
2995,50 |
3004,84 |
3004,31 |
2991,19 |
11 |
2972,53 |
2973,20 |
2959,55 |
2921,58 |
12 |
2996,82 |
3000,43 |
3002,81 |
2988,21 |
13 |
2969,61 |
3003,48 |
3006,03 |
2997,05 |
14 |
3010,00 |
3005,84 |
3004,31 |
2994,18 |
15 |
2991,22 |
3004,77 |
3001,63 |
2990,98 |
16 |
3005,58 |
3007,04 |
3005,86 |
2995,38 |
17 |
2877,30 |
3003,48 |
3006,03 |
2997,05 |
18 |
3018,05 |
3007,69 |
2963,72 |
2966,75 |
19 |
3001,86 |
3006,75 |
3005,11 |
2993,22 |
20 |
3001,92 |
3005,91 |
3001,30 |
2993,10 |
21 |
3001,92 |
3005,91 |
3001,30 |
2993,10 |
|
2992,140 |
3005,877 |
2999,262 |
2988,953 |
S |
30,321 |
13,178 |
13,471 |
19,131 |
2. Sprawdzanie, czy pomiary były obciążone błędami grubymi i ewentualne przeprowadzenie eliminacji lub korekty tych błędów.
Błędy grube powstają zazwyczaj wskutek pomyłki eksperymentatora (chociaż mogą być spowodowane również nieodpowiednią metodą pomiarową)
Po przeanalizowaniu wyników pomiarów można stwierdzić następujące błędy grube:
Student numer 1 - pomiar wysokości hb ,
Student numer 3 - pomiar boku b oraz wysokości hc ,
Student numer 11 - pomiar boków a, b i c ,
Student numer 13 - pomiar wysokości ha ,
Student numer 17 - pomiar wysokości ha ,
Student numer 18 - pomiar boku a ,
Wynik tych pomiarów (zaznaczone na czerwono) wykraczają poza przedział, w którym (zgodnie z funkcją Gaussa rozkładu gęstości prawdopodobieństwa) powinno znajdować się 99,7% wyników. Mogło to być spowodowane błędnym odczytem lub złym wyzerowaniem suwmiarki. Błędy te wpłynęły na wartość odchylenia standardowego. Ich skutkiem było także niedokładne obliczenie pól trójkątów.
Rezultaty pomiarów obarczonych błędami grubymi powinny zostać odrzucone, a pomiary należy powtórzyć. Postanowiłem więc dokonać korekty tych błędów i w ich miejsce wstawiłem wartość średnią danego pomiaru, gdyż jest ona o wiele bardziej wiarygodna. Nowe pomiary oraz wyniki pól trójkątów po korekcie przedstawia tabela 3 i 4.
Tabela 3 Pomiary boków i wysokości trójkąta nr 3 po korekcie
Numer Studenta |
a [mm] |
b [mm] |
c [mm] |
ha [mm] |
hb [mm] |
hc [mm] |
1 |
92,24 |
84,43 |
75,41 |
65,37 |
71,24 |
79,69 |
2 |
92,14 |
84,40 |
75,40 |
65,16 |
71,23 |
79,61 |
3 |
92,15 |
84,39 |
75,40 |
65,18 |
71,25 |
79,66 |
4 |
92,17 |
84,35 |
75,40 |
65,19 |
71,24 |
79,63 |
5 |
92,11 |
84,40 |
75,42 |
65,18 |
71,25 |
79,69 |
6 |
91,93 |
84,33 |
75,33 |
65,08 |
71,23 |
79,68 |
7 |
91,87 |
84,29 |
75,37 |
65,11 |
71,22 |
79,62 |
9 |
92,07 |
84,37 |
75,40 |
65,07 |
71,23 |
79,69 |
11 |
92,09 |
84,39 |
75,30 |
65,23 |
71,24 |
79,59 |
12 |
92,04 |
84,27 |
75,40 |
65,12 |
71,21 |
79,65 |
13 |
92,31 |
84,32 |
75,50 |
64,98 |
71,24 |
79,63 |
14 |
92,19 |
84,41 |
75,40 |
65,30 |
71,22 |
79,69 |
15 |
92,08 |
84,38 |
75,38 |
64,97 |
71,22 |
79,64 |
16 |
92,21 |
84,42 |
75,42 |
65,19 |
71,24 |
79,71 |
17 |
92,31 |
84,32 |
75,50 |
64,98 |
71,24 |
79,63 |
18 |
92,38 |
84,45 |
75,30 |
65,34 |
71,23 |
79,67 |
19 |
92,11 |
84,40 |
75,42 |
65,18 |
71,25 |
79,69 |
20 |
92,14 |
84,40 |
75,40 |
65,16 |
71,23 |
79,61 |
21 |
92,14 |
84,40 |
75,40 |
65,16 |
71,23 |
79,61 |
|
92,141 |
84,374 |
75,397 |
65,155 |
71,234 |
79,652 |
S |
0,123 |
0,049 |
0,051 |
0,111 |
0,011 |
0,036 |
*a,b,c- boki trójkąta, ha , hb , hc - wysokości prostopadłe do odpowiednich boków.
Tabela 4 Obliczenia pól trójkąta nr 4 po korekcie
Numer Studenta |
Pa [mm2] |
Pb [mm2] |
Pc [mm2] |
PH [mm2] |
1 |
3014,86 |
3007,40 |
3004,71 |
2995,82 |
2 |
3001,92 |
3005,91 |
3001,30 |
2993,10 |
3 |
3003,17 |
3006,39 |
3003,18 |
2993,02 |
4 |
3004,28 |
3004,55 |
3002,05 |
2992,35 |
5 |
3001,86 |
3006,75 |
3005,11 |
2993,22 |
6 |
2991,40 |
3003,41 |
3001,15 |
2985,68 |
7 |
2990,83 |
3001,57 |
3000,48 |
2984,93 |
9 |
2995,50 |
3004,84 |
3004,31 |
2991,19 |
11 |
3003,52 |
3005,97 |
2996,56 |
2988,89 |
12 |
2996,82 |
3000,43 |
3002,81 |
2988,21 |
13 |
2999,15 |
3003,48 |
3006,03 |
2997,05 |
14 |
3010,00 |
3005,84 |
3004,31 |
2994,18 |
15 |
2991,22 |
3004,77 |
3001,63 |
2990,98 |
16 |
3005,58 |
3007,04 |
3005,86 |
2995,38 |
17 |
2999,15 |
3003,48 |
3006,03 |
2997,05 |
18 |
3018,05 |
3007,69 |
2999,58 |
2995,18 |
19 |
3001,86 |
3006,75 |
3005,11 |
2993,22 |
20 |
3001,92 |
3005,91 |
3001,30 |
2993,10 |
21 |
3001,92 |
3005,91 |
3001,30 |
2993,10 |
|
3001,739 |
3005,162 |
3002,780 |
2992,402 |
S |
7,251 |
1,956 |
2,531 |
3,433 |
3. Analiza miar błędów przypadkowych.
Błędy przypadkowe są to błędy zmieniające się w sposób nieprzewidziany, zarówno co do wartości bezwzględnej jak i co do znaku, przy wykonaniu dużej liczby pomiarów tej samej wielkości w warunkach pozornie niezmiennych. W chwili pomiaru mierzącemu nie jest znana wartość błędów przypadkowych. Dopiero na podstawie wielu wyników pomiarów może on wyznaczyć ich parametry statystyczne.
Pomiary bezpośrednie boków i wysokości trójkąta są oczywiście obarczone błędem przypadkowym. Wpływ na to miały głównie:
- zaokrąglenia wierzchołków trójkąta
- trudność ustawienia mierzonej wysokości prostopadle do szczęk suwmiarki
- różne metody pomiaru
- różny ścisk suwmiarki stosowany przez mierzących
Z przeprowadzonych pomiarów wynikają następujące rzeczy:
- największe odchylenie standardowe w grupie pomiarów boków występuje przy pomiarze długości boku a, natomiast odchylenia standardowe boku b i c są porównywalne
- największe odchylenie standardowe w grupie pomiarów wysokości występuje przy pomiarze wysokości ha , a najmniejsze przy pomiarze wysokości hb, odchylenie standardowe wysokości hc jest nieco większe od odchylenia wysokości hb
- porównując odchylenie standardowe boku a oraz odchylenie wysokości ha można stwierdzić, że są one podobne
- porównując odchylenie boku b oraz odchylenie wysokości hb, łatwo zauważyć, że błąd przypadkowy boku b jest większy niż błąd przypadkowy wysokości hb
- porównując miarę błędu przypadkowego boku c oraz wysokości hc można stwierdzić, że odchylenie standardowe boku c jest nieznacznie większe od odchylenia wysokości hc
- błąd przypadkowy w grupie pomiaru boków jest większy niż błąd przypadkowy w grupie pomiaru wysokości
4. Analiza błędów systematycznych wyznaczenia powierzchni trójkąta numer 5.
Błędy systematyczne w pomiarach tej samej wartości pewnej wielkości, w niezmiennych warunkach, tym samym narzędziem i metodą pomiarową, przeprowadzonych przez tego samego obserwatora pozostają stałe.
Rozmiary obliczonych pól ze wzorów standardowych są bardzo zbliżone do siebie, natomiast pole trójkąta liczone za pomocą wzoru Herona jest nieco mniejszy od pozostałych trzech rezultatów. Może być to spowodowane tym, że do obliczania pola za pomocą wzoru Herona wykorzystuję się wartości wszystkich trzech boków trójkąta. Pomiary boków ze względu na trudności zmierzenia boku miały tendencję do zaniżania swej wartości. We wzorze tradycyjnym natomiast wykorzystuje się tylko jeden bok i opadająca na niego wysokość. Pomiary wysokości z kolei miały skłonność do zawyżania swej wartości.
Najmniejszy błąd przypadkowy zawierały pola liczone z wykorzystaniem boku b i wysokości hb, oraz boku c i wysokości hc
5. Zestawienie wyników pomiarów przedstawiają tabele 5 i 6.
Tabela nr 5
Wielkość mierzona |
[mm] |
S [mm] |
Sx= [mm] |
Δp=3Sx [mm] |
Δsuw. [mm] |
δp= [%] |
δn= [%] |
x ±p [mm] |
|
a |
92,141 |
0,123 |
0,028 |
0,084 |
0,03 |
0,092 |
0,032 |
92,14 |
|
b |
84,374 |
0,049 |
0,011 |
0,033 |
0,03 |
0,040 |
0,035 |
84,37 |
|
c |
75,397 |
0,051 |
0,012 |
0,036 |
0,03 |
0,048 |
0,040 |
75,40 |
|
ha |
65,155 |
0,111 |
0,025 |
0,075 |
0,03 |
0,120 |
0,046 |
65,16 |
|
hb |
71,234 |
0,011 |
0,003 |
0,009 |
0,03 |
0,013 |
0,042 |
71,23 |
|
hc |
79,652 |
0,036 |
0,008 |
0,024 |
0,03 |
0,030 |
0,038 |
79,65 |
|
Tabela nr 6
Wielkość mierzona |
[mm] |
S [mm] |
Sx= [mm] |
Δp=3Sx [mm] |
δp= [%] |
x ±p [mm] |
|
Pa |
3001,739 |
7,251 |
1,663 |
4,990 |
0,170 |
3001,74 |
|
Pb |
3005,162 |
1,956 |
0,449 |
1,346 |
0,045 |
3005,16 |
|
Pc |
3002,780 |
2,531 |
0,581 |
1,742 |
0,058 |
3002,78 |
|
PH |
2992,402 |
3,433 |
0,787 |
2,361 |
0,079 |
2992,40 |
|
Wyznaczenie minimalnej liczby pomiarów boków i wysokości, tak aby błąd przypadkowy był pomijalnie mały.
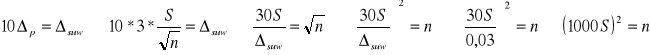
Tabela nr 7
|
a |
b |
c |
ha |
hb |
hc |
S |
0,123 |
0,049 |
0,051 |
0,111 |
0,011 |
0,036 |
n |
15129 |
2401 |
2601 |
12321 |
121 |
1296 |
S - odchylenie standardowe n -minimalna ilość pomiarów
WZORY
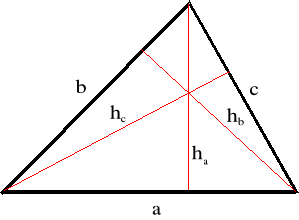
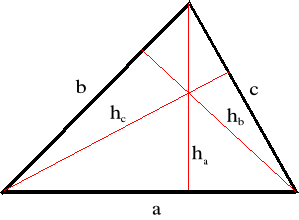
Rysunek
Wartość średniej arytmetycznej z n pomiarów
![]()
n - liczba pomiarów,
xi - wynik i-tego pomiaru
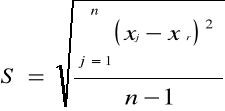
Odchylenie standardowe (odchylenie średniokwadratowe) wyników pomiarów od wartości średniej
xj - wynik j-tego pomiaru,
xśr - wartość średniej arytmetycznej
Wzór na pole trójkąta z wykorzystaniem jednego boku i padającej na niego wysokości
![]()
![]()
![]()
a, b i c - wymiary poszczególnych boków,
ha , hb i hc - wymiary poszczególnych wysokości,
Wzór Herona
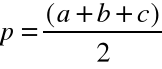
![]()
a, b i c - wymiary poszczególnych boków,
6. Odchylenie standardowe wartości średniej z n wyników o odchyleniu standardowym s.
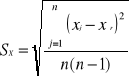
, czyli ![]()
PRZYKŁADOWE OBLICZENIA
Obliczenie Pa dla pomiaru numer 5 po korekcie,
a = 92,11 mm ha = 65,18 mm
![]()
mm2
Obliczenie Δp i δp dla wysokości hc
![]()
mm ![]()
![]()
mm
![]()
![]()
WYKRESY
Mając wyliczone odchylenie standardowe S dla poszczególnych pól można narysować funkcje rozkładu normalnego.
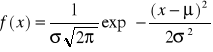
,gdzie ![]()
-odchylenie standardowe; ![]()
wartość oczekiwana
Dla Pa
2. Dla Pb
3. Dla Pc
4. Dla PH
WNIOSKI OGÓLNE
Podczas wykonywania ćwiczenia kilku studentów popełniło podczas pomiaru jednej z wielkości błędy grube, które to przy opracowywaniu wyników pomiarów zostały skorygowane. Błędy te mogły nastąpić z powodu własności geometrycznych mierzonego trójkąta (zaokrąglone wierzchołki) lub z winy mierzącego (nieprawidłowy odczyt, złe wyzerowanie suwmiarki itp.) W miejsce błędów grubych postanowiłem wpisać wartość średnią z pomiarów, gdyż jest ona o wiele bardziej wiarygodna (estymator wartości rzeczywistej) i bardziej odzwierciedla prawidłowy wynik pomiaru.
Większe błędy przypadkowe występują przy pomiarze boków trójkąta aniżeli przy pomiarze jego wysokości. Być może wynika to ze wspomnianych już wcześniej zaokrągleń wierzchołków trójkąta oraz z różnego sposobu ułożenia trójkąta w czasie pomiaru oraz z dociskania szczęk suwmiarki z różną siłą. Występujące błędy przypadkowe wpłynęły na obliczenie wartości pól. Porównując pola policzone tradycyjną metodą oraz pole wyliczone ze wzoru Herona, można stwierdzić, że pola są zbliżone do siebie, nie mniej jednak pole wyliczone z ostatniego wzoru odbiega nieco od Pol liczonych w sposób standardowy. Być może wynika to z tego, iż we wzorze ![]()
wykorzystywane są tylko dwie wartości zmierzone, natomiast we wzorze Herona należy użyć wszystkich wartości zmierzonych boków. Najmniejszy błąd przypadkowy zawierały pola liczone z wykorzystaniem boku b i wysokości hb, oraz boku c i wysokości hc.
Aby błąd przypadkowy średniej arytmetycznej był pomijalnie mały należy wykonać bardzo dużo pomiarów (Tabela 7). Najwięcej dla boku a oraz wysokości poprowadzonej na ten bok, a najmniej dla boku b oraz wysokości poprowadzonej na ten bok.
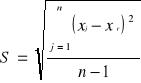
![]()
Wyszukiwarka
Podobne podstrony:
krzysztofik, W4 - elektroniki
3858, W4 - elektroniki
polak, W4 - elektroniki
krzysztofik, W4 - elektroniki
polak, W4 - elektroniki
1643, W4 - elektroniki
3334, W4 - elektroniki
1663, W4 - elektroniki
pomianek, W4 - elektroniki
zamojski, W4 - elektroniki
radosz, W4 - elektroniki
późniak-koszałka, W4 - elektroniki
7807, W4 - elektroniki
galar, W4 - elektroniki
piasecki, W4 - elektroniki
klink, W4 - elektroniki
borowiec, W4 - elektroniki
staniec, W4 - elektroniki
więcej podobnych podstron