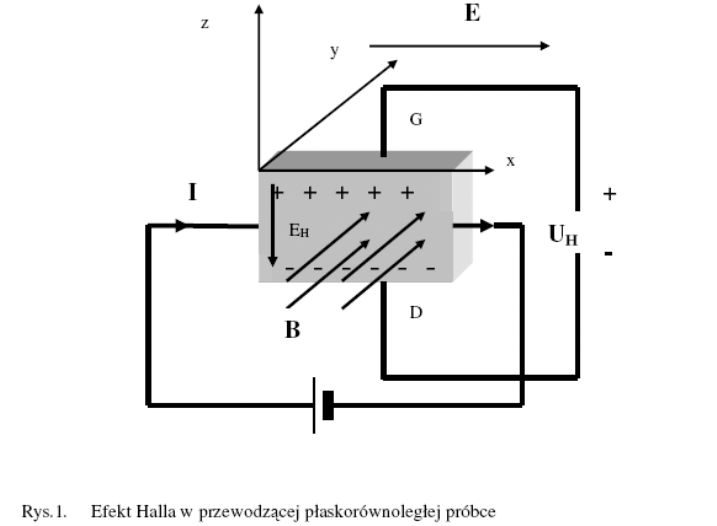
Efekt Halla w germanie

cel ćwiczenia

- ustalenie prawidłowości rządzących efektem Halla, wyznaczenie stałej Halla,

- wyznaczenie koncentracji i ruchliwości nośników prądu w germanie ( typu p lub n ),

- wyciągnięcie wniosków dotyczących rodzaju przewodnictwa w badanej próbce,

Cel ten osiągniemy analizując zależność napięcia Halla U_H od natężenia prądu I

przepływającego przez próbkę, gdy jest ona umieszczona w stałym polu magnetycznym o

indukcji B , lub zależności napięcia Halla U_H od wielkości indukcji B pola magnetycznego,

gdy przez próbkę przepływa prąd o stałym natężeniu I.

Oznaczenia

E_H - pole elektryczne powstające w próbce w wyniku efektu Halla

U_H - napięcie Halla

R_H - stała Halla, bądź współczynnik Halla

I - natężenie prądu płynącego przez próbkę

B - wartość indukcji pola magnetycznego

d - szerokość próbki

l - długość próbki

S - pole przekroju próbki

n - koncentracja elektronów (tzn. liczba elektronów w jednostce objętości)

p - koncentracja dziur (tzn. liczba ładunku dodatniego w jednostce objętości)

e - ładunek elektronu

μ - ruchliwość nośników

σ - przewodnictwo próbki

Efekt Halla

Materiały przewodzące, jak na przykład metale, czy półprzewodniki, których nośniki

ładunku mają różną od zera prędkość dryfu V, wykazują, w zewnętrznym polu magnetycznym ,tzw. efekt Halla. Polega on na powstawaniu pola elektrycznego E_H o kierunku poprzecznym do kierunku natężenia prądu I płynącego w próbce , jeśli badana próbka zostanie umieszczona w polu magnetycznym o indukcji B prostopadłej do kierunku I. Wynikiem powstałego, poprzecznego pola elektrycznego jest poprzeczny do kierunku przewodzenia spadek potencjału, dający tak zwane napięcie Halla U_H .

Jeżeli przez materiał przewodzący o kształcie płaskorównoległej płytki płynie prąd o natężeniu I (w kierunku dodatnim osi 0x), to wektor natężenia prądu pokrywa się z kierunkiem wektora natężenia pola elektrycznego E, które przyłożono wzdłuż próbki (rys 1).

Elektrony docierają do granic próbki i wraz z ich gromadzeniem się na powierzchni próbki

pojawi się w jej wnętrzu pole elektryczne E_H , a między punktami D i G powstaje różnica

potencjałów dająca tak zwane napięcie Halla U_H ( rys.1 ).

Parametry próbki

R₀ = 60Ω

S = (1 ± 0,1) * 10^-5 m²

d = (1 ± 0,1) * 10^-3 m

l = (0,02 ± 0,001) m

Układ pomiarowy

I - zasilacz (obwód zasilania badanej próbki)

II - zintegrowany Moduł badawczy z badaną próbką, zawierający wzmacniacz sygnału prądowego, cyfrowy miernik natężenia prądu sterującego próbką (miliamperomierz), oraz miernik temperatury próbki

III - elektromagnes (źródło pola magnetycznego)

IV - miernik indukcji pola magnetycznego (Teslametr)

V - czujnik pola magnetycznego (Hallotron)

VI - cyfrowy miernik napięcia Halla (miliwoltomierz)

VII - statyw mocujący Moduł z próbką umieszczoną pomiędzy nabiegunnikami elektromagnesu

Przebieg pomiaru

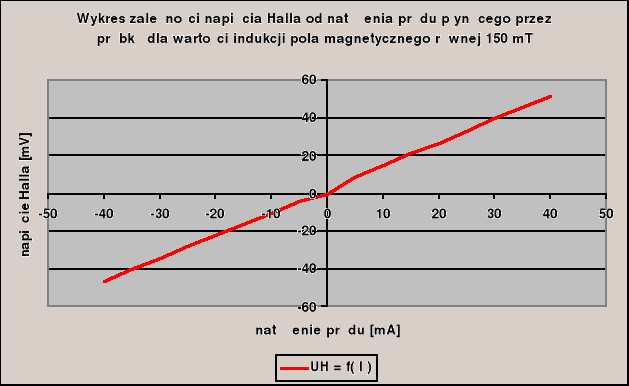
Pomiar U_H = f( I )

	UH [mV]
I [mA]	B = 150 mT	B = 80 mT
-40	-46,7	-21,2
-35	-40,3	-18,3
-30	-34,8	-15,7
-25	-27,7	-12,7
-20	-22,2	-9,8
-15	-16,6	-7,2
-10	-10,7	-4
-5	-4,3	-1
0	-0,2	-0,4
5	9	5,1
10	15,1	8,1
15	21	10,8
20	26,8	13,9
25	33	16,6
30	39,8	19,7
35	45,2	22,6
40	51,5	25,6

Wyznaczenie stałej Halla

U_H = ( R_H I B d ) / S / * S

U_H S = R_H I B d / * ( 1 / ( I S ) )

U_H / I = ( R_H B d ) / S

a = U_H / I

a = ( R_H B d ) / S / * ( S / ( B d ) )

R_H = ( a S ) / ( B d )

Korzystając z metody najmniejszych kwadratów wyznaczyliśmy wartość współczynnika a (współczynnik kierunkowy otrzymanej prostej)

dla B = 150 mT, a = 1.23 R_H1 = ( a S ) / ( B d ) = (1.23*10^-5)/(150*10^-3) = 8,2*10^-5 [m³/C]

B = 80 mT, a = 0,59 R_H2 = ( a S ) / ( B d ) = (0,59*10^-5)/(80*10^-3) = 7,38*10^-5 [m³/C]

wykresy

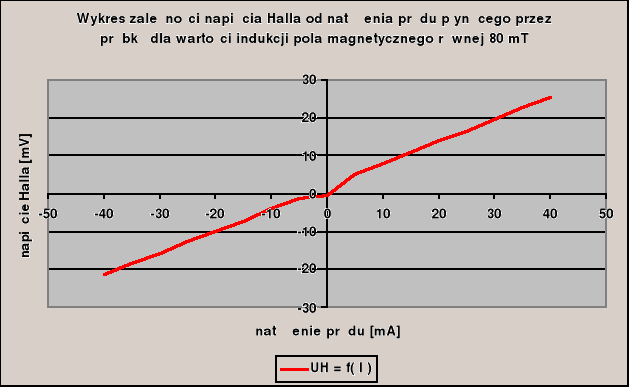
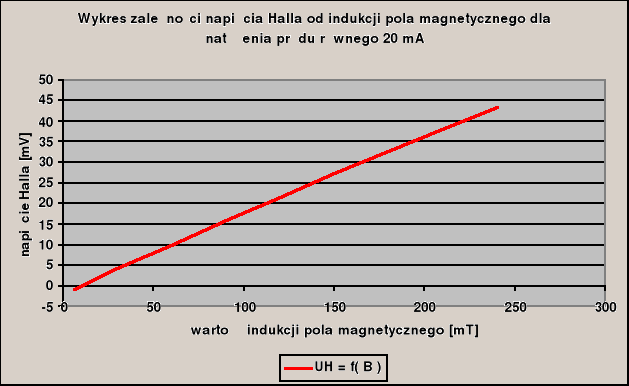
Pomiar U_H = f( B )

	UH [mV]
B [mT]	I = 20 mA	I = -30 mA
6	-0,8	5,6
30	4,2	-1,6
60	10,1	-9,9
90	16	-17,6
120	21,7	-26,3
150	27,2	-34,1
180	32,8	-41,8
210	38,1	-49
240	43,2	-56,3

Wyznaczenie stałej Halla

U_H = ( R_H I B d ) / S / * S

U_H S = R_H I B d / * ( 1 / ( B S ) )

U_H / B = ( R_H I d ) / S

a = U_H / B

a = ( R_H I d ) / S / * ( S / ( I d ) )

R_H = ( a S ) / ( I d )

Korzystając z metody najmniejszych kwadratów wyznaczyliśmy wartość współczynnika a (współczynnik kierunkowy otrzymanej prostej)

dla I = 20 mA, a = 0,19R_H3 = ( a S ) / ( I d ) = (0,19*10^-5)/(20*10^-3) = 9,5*10^-5 [m³/C]

I = -30 mA, a = -0,26 R_H4 = ( a S ) / ( I d ) = (-0,26*10^-5)/(-30*10^-3) = 8,7* 10^-5 [m³/C]

wykresy

Obliczenie koncentracji i ruchliwości nośników prądu

Koncentracja

e = 1,61 * 10^-19 C

R_H = 1 / ( p e )

stąd p = 1 / (R_H e )

p₁ = 1/ (8,2*10^-5 *1,61 * 10^-19) = 7,57*10²²

p₂ = 1/ (7,38*10^-5 *1,61 * 10^-19) = 8,41*10²²

p₃ = 1/ (9,5*10^-5 *1,61 * 10^-19) = 6,53*10²²

p₄ = 1/ (8,7*10^-5 *1,61 * 10^-19) = 7,14*10²²

Ruchliwość

σ = l / ( R₀ S ) = 0,02 m / ( 60Ω * 10^-5 m² ) = 33,3 [1/(Ω m)]

Nośnikami są dziury, więc μ = σ / ( p e )

μ₁ = 33,3 / (7,57 *10²²* 1,61*10^-19 ) = 2,73*10^-3

μ₂ = 33,3 / (8,41 *10²² * 1,61*10^-19 ) = 2,46*10^-3

μ₃ = 33,3 / (6,53 *10²² * 1,61*10^-19 ) = 3,17*10^-3

μ₄ = 33,3 / (7,14 *10²² * 1,61*10^-19 ) = 2,9*10^-3

wnioski

Napięcie Halla jest wprost proporcjonalne zarówno do natężenia prądu przepływającego przez próbkę, jak i do wielkości wektora indukcji magnetycznej pola magnetycznego, w którym umieszczono próbkę.

Znak nośników ładunku, decydujących o transporcie nośników, można określić na podstawie znaku stałej Halla, a więc także na podstawie znaku napięcia Halla, zaś wartość stałej Halla określa wielkość koncentracji nośników prądu.

We wszystkich rozpatrywanych przez nas przypadkach stała Halla jest dodatnia, co świadczy o tym, że nośnikami ładunku w germanie są dziury.

Wielkość indukcji pola magnetycznego podobnie jak wielkość prądu sterującego próbką, ma mały wpływ na wielkość stałej Halla. Im mniejsza indukcja pola magnetycznego lub natężenie prądu, tym mniejsza stała Halla.

Ze względu na to, że nośnikami ładunku w germanie są dziury, wnioskujemy, że badana próbka jest półprzewodnikiem.

---