1. CHARAKTERYSTYKA MODELU SOLOWA
Model Solowa dotyczy długookresowego wzrostu gospodarczego, jego źródeł i determinantów. Opisuje więc jak trzy czynniki wzrostu gospodarczego: kapitał (K), praca ludzka (N) i technologia (A) wpływają na przyrosty PKB. Zakłada się w nim, że ceny i płace są elastyczne (giętkie), a stopa deprecjacji kapitału jest stała. Postęp technologiczny zwiększa produktywność pracy ludzkiej jak i kapitału i dlatego często określany jest jako ogólna produktywność czynników produkcji. Związek między trzema poszczególnymi czynnikami wzrostu najlepiej pokazuje funkcja produkcji. Przy czym musi ona posiadać trzy własności: być rosnąca, w tempie malejącym o stałych korzyściach skali.
![]()
Funkcja produkcji jest funkcją rosnącą, gdy jej pierwsze pochodne są większe od zera. Pochodna funkcji produkcji po kapitale nazywana jest krańcową produktywnością kapitału, a pochodna funkcji produkcji po pracy nazywana jest krańcową produktywnością pracy:
![]()
Zwiększenie zastosowania jednego czynnika wytwórczego daje większy produkt, tzn.:
Szybkość zmian opisywanych przez funkcję jest malejąca (prawo malejącej produkcyjności krańcowej): ![]()
![]()
![]()
Wzrost jednego czynnika bez zmiany drugiego podnosi krańcową produkcyjność drugiego czynnika: ![]()
.
Ponadto można wyprowadzić dodatkową własność funkcji produkcji, a mianowicie, że pochodna funkcji![]()
jest równa krańcowej produkcyjności kapitału
![]()
Kolejną własnością funkcja produkcji, którą wykorzystuje się w modelu Solowa są stałe korzyści skali, tzn. zwiększenie nakładów obu czynników w tej samej proporcji α daje wzrost produktu w tej samej proporcji, tj:
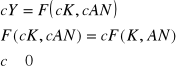
Jest to przypadek szczególny w klasie jednorodnych funkcji produkcji stopnia n, które spełniają warunek: ![]()
, dla t >0.
Dla funkcji produkcji, n=1, występują stałe korzyści skali.
Założenie stałych korzyści skali pozwala na przedstawienie funkcji w formie intensywnej, tzn. na jednego pracownika. Dzieląc obie strony równania funkcji produkcji przez liczbę pracowników uzyskujemy jej intensywną postać:
Y=F(K,N) / :N
![]()
Podstawiamy dla uproszczenia, że ![]()
, ![]()
,
![]()
A zatem intensywną postacią funkcji produkcji jest: y = ϕ(k).
![]()
Najczęściej wykorzystywaną przez nas funkcją w modelu Solowa będzie funkcja Cobba-Douglasa:
Charakteryzuje się ona wszystkim powyżej opisanymi własnościami.
Przy czym α jest elastycznością produktu wobec kapitału:
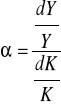
Z kolei (1-α) jest elastycznością produktu wobec pracy:
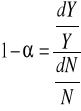
2. WYPROWADZENIE NAJWAŻNIEJSZYCH ZALEŻNOŚCI
Podstawowe zależności opisane w modelu możemy wyprowadzić z równania akumulacji kapitału. Określają one gospodarkę w stanie stacjonarnym. Proces ten przedstawimy w trzech etapach. Na początku nałożymy założenia, które znacząco uproszczą model. Następnie je uchylimy, co pozwoli rozszerzyć model.
Założenia dotyczące uproszczonej wersji modelu Solowa:
1. L (zasób siły roboczej) i N (zasób osób pracujących) są stałe.
2. Gospodarka jest zamknięta oraz brak jest ingerencji ze strony rządu.
3. Nie jest rozpatrywany wzrost technologii.
4. Jeśli N jest stałe, a technologii nie rozpatrujemy, to jednym czynnikiem wzrostu produkcji jest akumulacja kapitału.
Równowaga w długim okresie jest określona poprzez równanie akumulacji kapitału. Jeśli zasób pracy i technologia są stałe, to wzrost gospodarczy może pochodzić tylko od zmiany kapitału. Kapitał zmienia się dzięki inwestycjom oraz deprecjacji, co można formalnie zapisać:
![]()
![]()
![]()
![]()
![]()
Powyższe równanie opisuje równowagę, w punkcie, w którym kapitał się nie zmienia. Wówczas lewa strona równania, czyli oszczędności (równymi inwestycjom) równa się prawej (tj. niezbędne inwestycje odtworzeniowe). Kapitał na zatrudnionego rośnie (akumulacja kapitału na zatrudnionego), gdy inwestycje na zatrudnionego są większe od inwestycji odtworzeniowych na zatrudnionego. Wzrost kapitału na zatrudnionego z kolei jest źródłem wzrostu produkcji. Rosnąca produkcja w następnym okresie powiększa inwestycje dzięki wzrostowi oszczędności, co z kolei prowadzi do dalszego akumulowania kapitału. Proces powiększania produkcji na zatrudnionego trwa do momentu zrównania oszczędności z inwestycjami odtworzeniowymi:
Rysunek 1. Dynamika produkcji i kapitału w wersji uproszczonej modelu Solowa
Rysunek 1. jest graficzną ilustracją modelu Solowa jak również wcześniejszego równania. W punkcie k* zachodzi równowaga między inwestycjami a inwestycjami odtworzeniowymi. Przed punktem k* jest więcej inwestycji niż deprecjacji kapitału na pracownika. Nadwyżka inwestycji powoduje wzrost kapitału, co z kolei przybliża gospodarkę do punktu równowagi. Gdyby gospodarka znajdowała się po prawej stronie punktu równowagi, to inwestycje odtworzeniowe byłyby większe od faktycznych inwestycji. Spowodowałoby to ubytek kapitału i powrót do k*.
Po określeniu początkowych zależności możemy już rozszerzać model. Uchylamy więc założenia, które wcześniej zostały postawione. Jako pierwsze zostanie zmienione założenie dotyczące zatrudnienia, a następnie technologii. Zakładamy, że zatrudnienie zmienia się w tempie n, czyli ![]()
. W wyniku owej modyfikacji zmieni się równanie akumulacji kapitału. W celu wprowadzenia do modelu n, przekształcimy wzór na małe k.
Wiedząc, że ![]()
![]()
, można wyprowadzić K i Y.
![]()
![]()
Wykorzystując powyższe przekształcenia można już rozszerzyć wcześniejsze równanie akumulacji kapitału. W punkcie równowagi zachodzi więc warunek ![]()
, co można graficznie przedstawić:
Rysunek 2. Dynamika produkcji i kapitału w wersji pośredniej modelu Solowa
Przechodząc już do wersji rozszerzonej zakładamy, że zatrudnienie zmienia się w tempie n, czyli ![]()
, a technologia zmienia się w tempie a, czyli ![]()
. Pojawienie się technologii w rozpatrywanym modelu zmieni postać produkcji na zatrudnionego (produkcja na efektywną pracę), kapitału na zatrudnionego (kapitału na efektywnie zatrudnionego).
![]()
![]()
, można wyprowadzić K i Y.
![]()
![]()
Owa zmiana “wzbogaci” równanie akumulacji kapitału o tempo zmiany technologii.
W punkcie równowagi zachodzi warunek 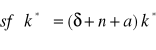
.
Rysunek 3. Dynamika produkcji i kapitału w wersji rozszerzonej modelu Solowa
Podsumowując, punkt równowagi w zależności od przyjętych założeń można zdefiniować jako:
![]()
![]()
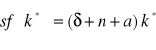
W momencie gdybyśmy chcieli zdefiniować zmiany produktu, jakie odbywają się w opisywanym powyżej punkcie, to okazuje się, że zasoby pracy i technologii rosną w tym samym tempie (nie ma zmian kapitałowych).
3. ZŁOTA REGUŁA KAPITAŁU
Na podstawie modelu Solowa można określić interesujące zależności między stopą oszczędności a kapitałem, czy produktem. Zmiana stopy oszczędności nie zmienia bowiem tempa wzrostu w długim okresie, a jedynie wpływa na odchylenia od trendu. Rozpatrzmy przypadek gdy zwiększamy poziom oszczędności. Przede wszystkim powoduje to przesunięcie punktu stacjonarnego i zwiększenie produkcji na zatrudnionego.
Rysunek 4. Dynamika produkcji i kapitału po wzroście stopy oszczędności s0<s1
Zmiana stopy oszczędności wywiera wpływ na poziom gospodarki a nie na jej wzrost. Zmienia się ścieżka zrównoważonego wzrostu, ale nie wpływa to na stopę wzrostu produktu na pracownika. W modelu Solowa tylko zmiana technologii wywołuje efekty w stopie wzrostu. Pozostałe zmiany powodują tylko modyfikację w poziomach. Przy czym zmiana poziomu zatrudnienia, czy technologii powoduje, że produkt spada z ścieżki i długookresowo zmienia jej bieg.
Ponadto na podstawie modelu, można zauważyć, że akumulacja fizyczna kapitału nie jest w stanie wyjaśnić dużych wzrostów poziomu PKB na jednego mieszkańca, ani też dużych różnic wielkości produktu między poszczególnymi krajami. Jedynie wzrost wydajności pracy może prowadzić do stałego wzrostu produktu na pracownika.
W końcu, model pozwala określić optymalny poziom oszczędności i maksymalną konsumpcje znając funkcję produkcji i elastyczności produktu wobec pracy i kapitału. Gdy w punkcie stacjonarnym wyznacza się maksymalną konsumpcję to jest to Złota Reguła Kapitału (ZRK).
Konsumpcja na zatrudnionego w stanie stacjonarnym stanowi, to, co pozostało z PKB po odjęciu oszczędności: ![]()
. Wówczas jej maksymalny poziom można określić, jako:
![]()
![]()
![]()
Ponieważ ![]()
, stąd ![]()
, czyli krańcowa produkcyjność kapitału musi równać się stopie deprecjacji.
Maksymalny poziom konsumpcji jest więc wtedy, gdy krańcowa produkcyjność kapitału (czyli styczna do ϕ(k*)) ma takie samo nachylenie (jest równoległa) jak krzywa inwestycji odtworzeniowych (czyli δ).
Równanie MPK=δ jest określane jako Złota Reguła Kapitału (dla wersji uproszczonej)
Dla wersji pośredniej modelu Solowa, analogicznie można wyprowadzić równanie na ZRK. Zakładając, że zatrudnienie zmienia się w tempie n, czyli ![]()
, a punkt równowagi charakteryzuje się równaniem: ![]()
ZRK ma postać MPK=δ+n
Przechodząc do wersji rozszerzonej również można określić równanie na ZRK. Zakładamy więc, że zatrudnienie zmienia się w tempie n, czyli ![]()
, a technologia zmienia się w tempie a, czyli ![]()
. W punkcie równowagi zachodzi zaś warunek: 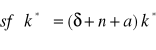
Wówczas równanie na Złotą Regułę Kapitału przybiera postać: MPK=δ+n+a
4. FORMUŁA WZROSTU MODELU SOLOWA
Zakładamy, iż funkcja produkcji ma postać: ![]()
. Ten zapis sugeruje, że technologia wpływa zarówno na pracę jak i kapitał, dlatego A jest też zwane współczynnikiem całkowitej produktywności czynników wytwórczych.
Z kolei przyrost powyższej produkcji jest równy:
![]()
Na podstawie powyższego równania możemy określić udziały kapitału i pracy w zmianie produktu. Gdy chcemy zinterpretować wpływ technologii na wzrost, to przekształcamy powyższe równanie i uzyskujemy, tzw. resztę Solowa:
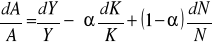
Na podstawie formuły wzrostu możemy określić nie tylko udziały zmian K, N, i A w zmianie produktu, ale też możemy pokazać czynniki determinujące tempo wydajności pracy. Przekształcamy wówczas równanie 2 do postaci:
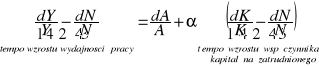
5. DEKOMPOZYCJA MODELU SOLOWA
![]()
Dekompozycja modelu Solowa wykorzystuje formułę wzrostu, by określić jakie jest wynagrodzenie za kapitał, pracę oraz technologię w produkcie. Widząc, że:
oraz, pamiętając, że:
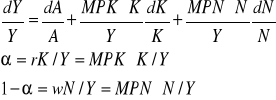
![]()
można przekształcić formułę wzrostu tak, by uzyskać dekompozycję Solowa:
6. STAN STACJONARNY
W stanie stacjonarnym wszystkie czynniki rosną w tym samym tempie. Dlatego musi być spełniona formuła wzrostu i równanie określające punkt stacjonarny, czyli:
![]()
![]()
Gdy FW=PS, to gospodarka jest w stanie stacjonarnym. By gospodarka była na ścieżce zrównoważonego wzrostu formuła wzrostu musi wynosić tyle samo, co warunek charakteryzujący punkt stacjonarny, czyli tempo wzrostu.
BEZROBOCIE
RYNEK PRACY I JEGO ELEMENTY
Rynek pracy, to mechanizm dopasowań podaży i popytu na pracę. Dopasowania wyrażają warunki na jakich dokonuje się transakcja między osobami oferującymi pracę (pracobiorcami), za określoną płacę a jej nabywcami (pracodawcami). Przedmiotem wymiany jest sprzedaż - kupno czynnika produkcji, którym jest praca.
Rynek pracy jest kształtowany przez decyzje podejmowane przez gospodarstwa domowe, przedsiębiorstwa i rząd. Elementami rynku pracy są więc: popyt na pracę, podaż pracy i płaca realna. Popyt na pracę, to zapotrzebowanie na pracę zgłoszone przez przedsiębiorstwa. Przedmiotem transakcji jest praca, za którą płaca określoną płacę.
Determinanty popytu na pracę:
popyt i ceny na rynku produktów i usług przedsiębiorstwa
technologia (efekt wypierania i kompensacji)
cena kapitału i pracy
Z punktu widzenia przedsiębiorstwa, który dąży do maksymalizacji zysku, granicą zatrudnienie nowego pracownika jest zrównanie się jego płacy realnej (W/P) z krańcową produktywnością pracy (MPN). Wówczas funkcja popytu na pracę, ma postać: W/P = MPN(ND)
Krzywa popytu na pracę jest ujemnie nachylona w stosunku do płac realnych.
Podaż pracy to punkt widzenia ludzi chętnych do pracy. Pracę sprzedają na rynku pracy gospodarstwa domowe. Dokonują one maksymalizacji swojej korzyści poprzez optymalny podział czasu między pracę zarobkową a czasem wolnym.
Determinantami podaży pracy są:
preferencji osób dotyczących pracy i czasu wolnego
wysokości wynagrodzenia za jednostkę oferowanej pracy
dostępu do innych dochodów
aktywności zawodowej innych członków gospodarstwa domowego
czynniki demograficzne i społeczne
sytuacji na rynku pracy
Krzywa podaży pracy jest nachylona dodatnio, gdyż wyraża zależność: im wyższa płaca, tym większa podaż pracy (efekt substytucyjny). Gdy jednak dochód na jednostkę jest bardzo wysoki, to może pojawić się efekt dochodowy. Oznacza on, że czas wolny jest wartością ważniejszą niż możliwość osiągnięcia dodatkowego dochodu. Krzywa podaży reaguje wówczas negatywnie na wzrost płac.
2. BEZROBOCIE RÓWNOWAGI
Równowaga na rynku pracy zachodzi, gdy ND=NS. Punktem równowagi jest przecięcie się krzywych popytu i podaży pracy, w którym poziom płac zadawala pracowników i pracodawców. W punkcie E ustala się pełne zatrudnienie.
Krzywe popytu i podaży pracy mogą się przesuwać pod wpływem swoich determinantów. Przesunięcie jednej lub obu krzywych wyznacza nowy punkt równowagi na rynku pracy, a więc nowy poziom zatrudnienia i płac realnych.
Z kolei nierównowadze na rynku pracy towarzyszy bezrobocie. Na rynku występuje przede wszystkim bezrobocie faktyczne, mierzone liczba bezrobotnych lub stopą bezrobocia oraz bezrobocie równowagi najczęściej kojarzone z pełnym zatrudnieniem.
By ustalić poziom bezrobocia w równowadze można go przeanalizować od strony zasobowej lub strumieniowej. W pierwszym wypadku podaje się liczby pod koniec okresu badawczego (np. roku, kwartału, czy miesiąca). W drugim przypadku analizuje się odpływy i dopływy między zasobami pracy i bezrobocia. Zostało to pokazane na poniższym rysunku.
Jak wynika z powyższego rysunku są dwa strumienie: dopływu do bezrobocia z zasobów pracy (b) i odpływu z bezrobocia do zasobów pracy (e):
OT- Osoby tracące pracę
OZ- Osoby znajdujące pracę
Wówczas zmianę w zasobie bezrobotnych można zapisać jako:
Zaś naturalną stopę bezrobocia należy zdefiniować jako:
Z kolei miarą bezrobocia faktycznego na danym rynku pracy jest stopa bezrobocia, czyli stosunek liczby bezrobotnych (U) do siły roboczej (L): u=U/L
Bezrobocie naturalne jest częścią bezrobocia faktycznego i stanowi pewien nieunikniony i niezbędny dodatni poziom bezrobocia towarzyszący rozwijającej się gospodarce. Wiąże się ono z naturalną dynamiką procesów zachodzących na rynku pracy, czyli powstawania nowych i likwidowania już istniejących miejsc pracy oraz ze zmianą aktywności siły roboczej. W współczesnej ekonomii znane są dwie teorie bezrobocia równowagi: bezrobocie naturalne oraz NAIRU.
W latach osiemdziesiątych za sprawą R. Layarda, S. Nickella i R. Jackmana zrodziła się inna teoria bezrobocia równowagi zwana NAIRU (non-accelerating inflation rate of unemployment). Dotyczy ona bezrobocia, które pojawia się w momencie, gdy wynegocjowane płace realne odpowiadają płacom zgodnym z realiami gospodarczymi, czyli gdy ustabilizuje się dynamika procesów inflacyjnych. Naturalna stopa bezrobocia ustala się na takim poziomie, na którym żądania płacowe pracowników i pracodawców są niesprzeczne, dzięki czemu nie wywierają one wpływu na inflację. Poziom NAIRU zależy więc od poziomu płacy realnej i postulowanych płac.
Wpływ wielkości płac postulowanych i realnych na wielkość NAIRU został przedstawiony na poniższym rysunku. Krzywa PR0 określa poziom płac realnych, który odpowiada możliwościom ekonomicznym gospodarki. Jej położenie zależy przede wszystkim od wydajności pracy. Krzywa PP0 obrazuje poziom płac postulowanych, zaś jej położenia zależy, z kolei, od wielkości stopy bezrobocia. W sytuacji, gdy oczekiwania płacowe są większe niż płace realne dochodzi do przyśpieszenia procesów inflacyjnych. Odwrotnie byłoby, gdyby płace postulowane były mniejsze niż realne. W momencie zrównania się obu wielkości następuje stabilizacja procesów inflacyjnych, której odpowiada określony poziom NAIRU. Na rysunku jest to zilustrowane w punkcie A. Poziom równowagi pod wpływem swoich determinantów ulega jednak zmianom. Dzieje się tak wówczas, gdy wzrasta wydajności pracy. Wpływa to bowiem na wzrost płac realnych, co jest widoczne przez przesunięcie w górę prostej PR0 do poziomu PR1. W rezultacie ustala się nowy punkt równowagi B, któremu odpowiada niższy poziom NAIRU n0. Podobny efekt można uzyskać, gdy przy niezmienionym poziomie płacy realnych PR0, uda się przesunąć krzywą płac postulowanych z poziomu PP0 do PP1. Wówczas również ustaliłby się nowy punkt równowagi C, któremu odpowiadałaby niższa stopa bezrobocia. Idealna sytuacja pojawiłaby się w momencie zaistnienia obu powyższych procesów, czyli gdyby wzrostowi płac realnych towarzyszyło osłabienie presji płacowej. Ilustruje to punkt równowagi D, któremu odpowiadałby najniższy poziom NAIRU n1.
Poziom NAIRU nie jest stały i może ulec zmianie pod wpływem determinantów określających wielkość realistycznych i postulowanych płac realnych negocjowanych przez pracowników i pracodawców. Podstawowym czynnikiem, który kształtuje poziom płac realnych odpowiadający realiom ekonomicznym gospodarki jest wydajność pracy, czyli miara produktywności pracy oraz wysokość negocjowanych płac i siła presji płacowej.
Kwiatkowski E., Bezrobocie. Podstawy teoretyczne, str. 152, PWN, Warszawa 2002.
SKRYPT Z MAKROEKONOMII, CZĘŚĆ I
SKRYPT STANOWI POMOC DO WYKŁADU Z MAKROEKONOMII NA POZIOMIE ŚREDNIOZAAWANSOWANYM. SKŁADA SIĘ Z DWÓCH CZEŚCI. PIERWSZA DOTYCZY DŁUGIEGO OKRESU, A DRUGA KRÓTKIEGO. NA POCZATKU OMÓWIONY ZOSTAŁ MODEL SOLOWA, JEGO GŁÓWNE ZAŁOŻENIA, WNIOSKI I KONSEKWENCJE. NASTĘPNIE PRZEDSTAWIONO PROBLEM BEZROBOCIA W DŁUGIM OKRESIE.
W CZĘŚCI DRUGIEJ SKUPIONO SIĘ NA DWÓCH MODELACH: IS-LM I AS-AD. PRZY CZYM PRZEANALIZOWANO JE DLA GOSPODARKI ZAMKNIĘTEJ I OTWARTEJ.
PIERWSZA CZEŚĆ SKRYPTU DOTYCZY WYKŁADU I ĆWICZEŃ.
SZKOŁA GŁÓWNA HANDLOWA
KOLEGIUM ZARZĄDZANIA I FINANSÓW
KATEDRA HISTORII MYŚLI EKONOMICZNEJ
SALA 1115A, BUDYNEK F
rwojcie@sgh.waw.pl
WARSZAWA 2009 ROK
RENATA WOJCIECHOWSKA
STUDIA NIESTACJONARNE
SKRYPT Z MAKROEKONOMII,
CZĘŚĆ I
2009 ROK
![]()
![]()
k
y
k*
![]()
![]()
![]()
k
y
k*
![]()
![]()
![]()
k
y
k*
![]()
![]()
![]()
k
![]()
![]()
![]()
k0*
k1*
![]()
![]()
![]()
Poziom płacy
realnej (Wr)
wr
ND
N1
Zatrudnieni (N)
wr1
Poziom płacy
realnej (Wr)
wr
ND
N1
Zatrudnieni (N)
Efekt dochodowy
E
wr1
NE
Zasób zatrudnionych (N)
Poziom płacy
realnej (Wr)
ND
NS
PRACUJĄCY
(N)
BIERNI
(B)
BEZROBOTNI
(U)
NB
UB
BU
UN
NU
BN
![]()
![]()
![]()
![]()
NAIRU
Płaca realna
W0/P1
W0/P0
n1
n0
D
B
C
A
PR1
PR0
PP0
PP1
Wyszukiwarka
Podobne podstrony:
SKRYPT Z MAKRO, Wykłady rachunkowość bankowość
CW. Z MAKRO, Wykłady rachunkowość bankowość
makroekonomia 2 Pacho - skrypt, Wykłady rachunkowość bankowość
PMikro cw, Wykłady rachunkowość bankowość
Hipoteza o istotności parametrów strukturalnych, Wykłady rachunkowość bankowość
pytania 67-72 +132, Wykłady rachunkowość bankowość
pyt egz makra, Wykłady rachunkowość bankowość
MAKROEKONOMIA, Wykłady rachunkowość bankowość
91-96, Wykłady rachunkowość bankowość
36-42, Wykłady rachunkowość bankowość
POLITYKA REGIONALNA-ŚCIĄGI, Wykłady rachunkowość bankowość
Pytania egzaminacyjne Zarządzanie, Wykłady rachunkowość bankowość
85-90, Wykłady rachunkowość bankowość
Zakres pracy zaliczeniowej do OKiWP, Wykłady rachunkowość bankowość
socjologia, Wykłady rachunkowość bankowość
więcej podobnych podstron