Wojskowa Akademia Techniczna
im. Jarosława Dąbrowskiego

Laboratorium Fizyki Ogólnej

Sprawozdanie z ćwiczenia laboratoryjnego

Nr 31

Tytuł: Wyznaczanie stałej Rydberga i stałej Planca z widma liniowego wodoru.

Wykonał: Paweł Wojno gr. C04H Warszawa dnia: 15.12.2004r

Prowadzący zajęcia: mgr inż. Piotr Marciniak

Ocena przygotowania do zajęć:……….……………………..

Ocena końcowa:………………………………

I Opis teoretyczny

Dostarczając energię do atomu można doprowadzić do jego wzbudzenia. Wzbudzony atom charakteryzuje się tym, że jego elektrony znajdują się na orbitach bardziej oddalonych od jądra niż w stanie podstawowym. Po pewnym czasie elektrony wracają do któregoś ze stanów położonych bliżej jądra (np. do stanu podstawowego), czemu towarzyszy emisja promieniowania elektromagnetycznego. Wybór danego przejścia, gdy istnieje kilka ich możliwości, następuje w sposób statystyczny.

Każdy pierwiastek, którego atomy przechodzą od stanu wzbudzonego do potencjalnie niższego emituje energię promienistą w szczególny, właściwy tylko dla siebie, sposób. Rozkład tej energii nazywany jest widmem liniowym

Wyjaśnienia tego zjawiska podjął się Niels Bhor wprowadzając 3 postulaty (postulaty Bhora).

I postulat Bohrna (stacjonarnych stanów atomu) zakłada, że istnieje tzw. stacjonarne stany atomu, w których elektron, wbrew regułom fizyki klasycznej, nie emituje promieniowania W stanie stacjonarnym elektrony poruszają się w atomie po pewnych orbitach i nie wysyłają fal elektromagnetycznych.

II postulat Bohra (stacjonarnych orbit kwantowych) podaje sposób obliczania orbit elektronowych, odpowiadających stanom stacjonarnym Zgodnie z tym postulatem elektron nie może poruszać się w atomie po dowolnych orbitach, lecz tytko po takich, dla których moment pędu elektronu L jest całkowitą wielokrotnością wielkości ћ („kreślonej" stałej Plancka):

gdzie
jest stałą Plancka

n=1,2,3,….. (1.1)

Dla orbit kołowych

(1.2)

gdzie:
- masa elektronu.
- wartość orbitalnej prędkości elektronu na n-tej orbicie,
- promień n-tej orbity elektronowej

Tak więc drugi postulat Bohra przyjmuje postać

(1.3)

III postulat Bohra (częstotliwości) dotyczy energii emitowanej przez atom, który przechodząc ze stanu wzbudzonego o energii
do stanu o mniejszej energii
wypromieniowuje foton Energia fotonu E jest przy tym równa różnicy energii atomu w stanie początkowym i końcowym

(1.4)

Jak wiadomo, energię fotonu E i częstotliwości emitowanego promieniowania v łączy zależność

(1.5)

Trzeci postulat Bohra przyjmuje więc postać

(1.6)

W ujęciu klasycznym warunkiem ruchu elektronu wokół jądra jest równość siły odśrodkowej i siły przyciągania elektrostatycznego:

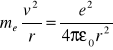
stąd energia kinetyczna elektronu:

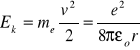
(1.7)

Z II postulatu Bohra (1.3) wynika, że pęd elektronu
. Obliczając stąd energię kinetyczną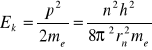
Z porównania ze wzorem (1 7) wynika, że:

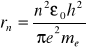
n=1,2,3,… (1.8)

Potencjał pola elektrycznego wokół Jądra wodoru wynosi
. Energia potencjalna elektronu w tym polu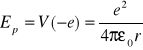
Energię całkowitą elektronu ( E ) otrzymujemy dodając do niej energię kinetyczną wyrażoną wzorem (1.7) :

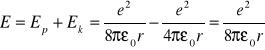
(1.9)

Podstawiając za r wyrażenie (1.8) otrzymujemy energię całkowitą elektronu w zależności od numeru orbity dozwolonej liczonej w kierunku od jądra atomu:

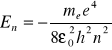
(1.10)

Widzimy więc. że wprowadzenie drugiego postulani Bohra spowodowało skwantowanie energii. Energia elektronu może przyjmować tylko wartości dyskretne określone naturalną liczbą n nazywaną główną liczbą kwantową Określa ona liczbę porządkową poziomu energetycznego lub numer stacjonarnej orbity elektronu.

Jak wynika ze wzoru (1.10). wraz ze zwiększaniem głównej liczby kwantowej n (czyli w miarę wzrostu promienia dozwolonej orbity) energia elektronu w atomie rośnie (maleje przy tym lej bezwzględna wartość) Maksymalna energia elektronu w atomie Jest równa zeru. Odpowiada to n = ∞ czyli oderwaniu elektronu od jądra (jonizacji atomu), Stan odpowiadający n=l. w którym elektron znajduje się najbliżej jądra, nazywamy stanem podstawowym atomu. Stany odpowiadające wszystkim pozostałym wartościom n > l noszą nazwę stanów wzbudzonych.

Zgodnie z trzecim postulatem Bohra (1.6) przejściu elektronu z orbity wyższej o energii
na niższą o energii
(n > k) wy promieniowany foton będzie miał energię

r

Z czego po uwzględnieniu zależności (1.10) oraz tego, że
otrzymujemy wzór na długość wypromieniowanej fali:

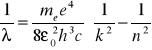
.. (1.12)

Współczynnik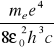
nazywamy stałą Rydberga dla atomu wodoru i oznaczamy
.

Znając stałą Rydberga można wyznaczyć stałą Plancka:

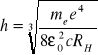
(1.12)

Należy Jednak zwrócić uwagę na fakt. że stała Plancka jest stałą fizyczną uniwersalną (tzn. zacho­wuje swoją wartość we wszystkich zjawiskach kwantowo-mechanicznych). Natomiast stała Rydberga jest stała tylko dla zjawisk zachodzących wewnątrz atomu wodoru.

W ćwiczeniu atomy wodoru są wzbudzane wyładowaniami elektrycznymi w objętości Widzialne linie widmowe należą do tzw. serii Balmera odkrytej doświadczalnie w 1885r powstałą podczas przejść elektronów z wyższych orbit na orbitę drugą:

(1.13)

Są to cztery linie:

czerwona odpowiadająca przejściu 3
2

niebieska odpowiadająca przejściu 4
2

fioletowa odpowiadająca przejściu 5
2

fioletowa odpowiadająca przejściu 6
2

II Opis układu pomiarowego

Źródłami światła w tym ćwiczeniu są gazy świecące (hel i wodór) w rurkach Geislera. Wzbudzenie atomów gazów uzyskuje się poprzez przyłożenie do elektrod rurek Geislera wysokiego napięcia z induktora Ruhmkorffa. W związku z tym nie wolno dotykać przewodów połączonych z wtórnym uzwojeniem induktora w czasie jego pracy.

Widmo promieniowania badanego gazu zawartego w rurce pada na szczelinę wejściową monochromatora Hilgera Monochromatorem nazywamy przyrząd, który wycina promieniowanie monochromatyczne z padającego na szczelinę wejściową światła, W związku z tym w okularze nie będziemy obserwowali jednocześnie całego widma, tylko jego poszczególne fragmenty Wybór fragmentu widma, który chcemy obserwować, dokonywany jest za pomocą śruby z podziałką. Przekręcając Ją możemy zobaczyć w okularze całe badane widmo leżące w obszarze widzialnym

Chcąc wykonać analizę widmową świecącego wodoru, musimy dokładnie wyznaczyć długości fal poszczególnych linii. Aby to zrobić, należy najpierw wyznaczyć dla stosowanego spektrometru (bądź monochromatora) krzywą aparaturową, zwaną krzywą dyspersji, używając pierwiastka o znanym widmie W ćwiczeniu jest nim hel posiadający wiele widzialnych prążków Krzywa dyspersji jest zależnością rzeczywistej długości fali od odczytanego z aparatury położenia linii. Obie te wielkości nie są sobie równe z powodu nieidealności ustawienia i wyskalowania pryzmatu pomiarowego.

III wykonywane czynności

A. Wykreślenie krzywej dyspersji

Wyznaczanie długości fali dla poszczególnych numerów linii i zapisywanie pomiarów w tabelce:

numer linii	1	2	3	4	5	6	7
długość fali[nm]	667,8	587,6	504,8	492,2	471,3	x	447,1
Barwa	czerwona	żółta	zielona	zielona	niebieska	niebieska	fioletowa
Intensywność	silna	słaba	słaba	silna	słaba	słaba	średnia
S(od siebie)[nm]	x	584,0	498,4	x	x	x	x
S(do siebie)[nm]	x	585,0	498,0	x	x	x	x
[nm]	x	584,5	498,2	x	x	x	x

x oznaczaj te pomiary których nie byliśmy w stanie zmierzyć z powodu zużycia rurki wypełnionej He.

B. Wyznaczenie długości fali w widmie wodoru

Wyznaczanie długości fali dla poszczególnych linii i zapisywanie pomiarów w tabelce:

Linie widma
długość fali [nm]	656,2	466,1	434,0	410,7
barwa	czerwona	niebieska	fioletowa	fioletowa
s(od siebie) [nm]	652,0	461,0	432,4	x
s(do siebie) [nm]	651,0	460,6	433,5	x
[nm]	651,5	460,8	432,9	x

IV. Obliczenia

Wyliczamy wartość średnią S z pomiarów na widmie helu i wodoru.

Na podstawie wzoru (1.13) wyznaczamy stała Rydberga dla każdej linii wodoru.

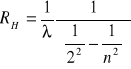
A następnie wyznaczamy wartość średnia (
) naszych obliczeń.

Uzyskana wartość (
) podstawiamy do wzoru (1.12) i obliczamy wartość stałej Planca. Od obliczeń wykorzystujemy wartości uzyskane z tablic fizycznych gdzie:

i zakładamy ze wartości te nie są obarczone błędami.

Do obliczenia błędu wyznaczenia stałej Rydberga stosujemy wzór na błąd względny

i wykorzystujemy fakt że:

W celu wyznaczenia wartości granicznego błędu bezwzględnego (
) mnożymy błąd względny przez stała Rydberga.

Przez wybranie największej wartości bezwzględnej, spośród uzyskanych błędów, uzyskujemy graniczny błąd bezwzględny wyznaczenia średniej wartości stałej Rydberga.

Błąd graniczny na wyznaczenie stałej Plancka obliczmy na podstawie wzoru:

W celu wyznaczenie błędu bezwzględnego stałej Plancka (
), postępujemy analogicznie jak w przypadku wyznaczania błędu bezwzględnego stałej Rydberga. Mamy wtedy że :

Tabela w punkcie V zawiera wyniki wszystkich obliczeń.

V. Tabele z wynikami

Niestety wyznaczenie krzywej dyspersji okazało się nie możliwe z powodu zbyt małej ilości udanych pomiarów. Dzięki temu ze dysponowaliśmy rzeczywistymi wartościami długości fal dla poszczególnych widm falowych mogliśmy osiągnąć cel naszego doświadczenia.

Linie widma
długość fali [nm]	656,2	466,1	434,0	410,7
barwa	czerwona	niebieska	fioletowa	fioletowa
S(od siebie) [nm]	652,0	461,0	432,4	x
S(do siebie) [nm]	651,0	460,6	433,5	x
[nm]	651,5	460,8	432,9	x
błąd względny	7,1625·	11,3710·	2,4194 ·	x
błąd bezwzględny	7,8588	13,0112	2,6545
	1,0972·	1,1442·	1,0972·	x
Średnie-	1,1129·	Stała Plancka h[Js]	6,5951·
graniczny błąd względny-	11,3710·	Graniczny błąd względny	3,7903·
graniczny błąd bezwzględny	13,0112	graniczny błąd bezwzględny	2,4998

VI. Wnioski

Celem naszego doświadczenia było wyznaczenie stałej Rydberga i stałej Plancka dla widm wodoru. Cel ten został osiągnięty, mimo iż nie byliśmy w stanie wyznaczyć krzywej dyspersji.

Nie byliśmy w stanie wyznaczyć krzywej dyspersji z powodu zbyt małej ilości wyznaczonych długości fal widm helu. Było to spowodowane zużyciem aparatury na której wykonywane było doświadczenie.

Nie wyznaczyliśmy długości fali dla poszczególnych linii wodoru z krzywej dyspersji. Wartości te zostały już wcześniej podane i na ich podstawie dokonaliśmy obliczeń mających na celu wyznaczenie stałej Rydberga i stałej Plancka.

Ostatecznie otrzymaliśmy wyniki:

Stała Rydberga wynosi 1,1129·
i jest obarczona błędem rzędu 13,0112

Stała Plancka wynosi: 6,5951·
Js i jest obarczona błędem rzędu 2,4998

Musimy się jednak liczyć z wystąpieniem błędów systematycznych spowodowanych zużyciem aparatury na której było wykonywane doświadczenie. Generalnie cel doświadczenia został osiągnięty.

- 7 -

---