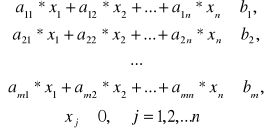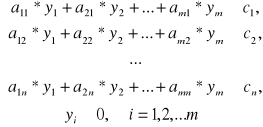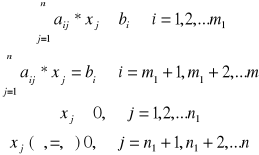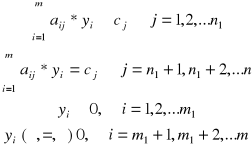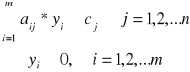Lekcja 5. Dualność zadań programowania liniowego. Wykorzystanie estymatorów w analizie rozwiązania zadania programowania liniowego.

5.1. Ekonomiczny sens dwoistości zadań programowania liniowego.

5.2. Właściwości dualnych zadań programowania liniowego.

5.3. Wykorzystanie estymatorów w analizie rozwiązania zadania programowania liniowego.

5.1. Ekonomiczny sens dwoistości zadań programowania liniowego.

Z każdym zadaniem programowania liniowego sprzężone jest pewne inne zadanie PL zwane zadaniem dualnym (dwoistym).

Dualność w planowaniu liniowym rozpatrujemy na przykładzie zadania optymalnego wykorzystania surowców.

Zadanie pierwotne. . Przedsiębiorstwo ma możliwość produkować n rodzaje produkcji. W trakcie ich wytwarzania wykorzystuje m różnych surowców. Przedsiębiorstwo dysponuje i-m z surowców w ilości b_i jednostek (i=1,2,...m). Dla produkcji jednej jednostki przemysłowej produkcji rodzaju j (j=1,2,...,n) potrzeba odpowiednio surowców w ilości: pierwszego - а_1j , drugiego - a_2j , j-go - a_3j (j=1,2,...,m). Planowy zysk przedsiębiorstwa w realizacji jednej jednostki produkcji rodzaju j (j=1,n) wynosi с_j pieniężnych jednostek.

Zapisać ekonomiczno - matematyczny model zadania, pozwalający znaleźć zbilansowany według zasobów plan wyprodukowania produktów oraz gwarantujący przedsiębiorstwu maksymalny zysk;

Jeżeli wprowadzić zmienne х_j — ilości produkcji j-go rodzaju, wtedy matematyczny model zadania ma postać:

max Z = c₁*x₁ + c₂*x₂ + ... + c_n*x_n (5.1)

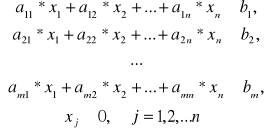
(5.2)

Przypuścimy dalej, że przedsiębiorstwo dla produkowania swojej produkcji kupuje surowce i innego przedsiębiorstwa (zaznaczymy jego jako Przedsiębiorstwo 2). Potrzebnie ustalić przykładowe ceny na surowce. Ceny surowców zaznaczymy y₁, y₂, ... , y_m. Jasne, że interesy pierwszego i drugiego przedsiębiorstwa są różne. Dla tego ceny zakupu surowców u przedsiębiorstwa 2 powinny spełnić niektóre warunki:: 1) przedsiębiorstwo 1 pragnie zminimalizować ogólne koszty surowców zakupionych u przedsiębiorstwa 2; 2) przedsiębiorstwo 2 będzie sprzedawało surowce tylko za takie ceny, żeby dochód od sprzedaży surowców był nie mniejszy, niż cena wyprodukowanej z niego produkcji (inaczej dla czego sprzedawać, jeżeli można na przedsiębiorstwie 2 zorganizować taką produkcje)

Takie zapotrzebowania ze strony 1-go i 2-go przedsiębiorstw można zapisać w postaci ZPL.

Zapotrzebowanie 1 przedsiębiorstwa 1 (konsumenta) — minimalizacja kosztów zakupu surowców:

min f = b₁*y₁ + b₂*y₂ + ... + b_m*y_m (5.3)

Zapotrzebowanie 2 przedsiębiorstwa 2 (sprzedawcy) można zapisać w postaci układu ograniczeń. Przedsiębiorstwo 2 nie będzie produkować jednostkę produkcji pierwszego rodzaju, jeżeli

a₁₁*y₁ + a₂₁*y₂ + ... +a_m1*y_m ≥ c₁

gdzie lewa część nierówności oznacza dochód od sprzedaży surowców przedsiębiorstwem 2, które potrzebne dla produkcji jednostki produkcji, prawa strona — cena jednostki produkcji na przedsiębiorstwie 1.

Analogiczne możemy zapisać ograniczenia dla innych rodzaje produkcji. Wtedy zapotrzebowania przedsiębiorstwa 1 można formalnie zapisać w postaci układu ograniczeń:

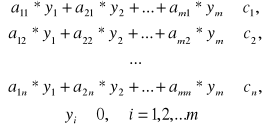
(5.4)

Zmienne y_i (i=1,2,...m) nazywają się ocenami (estymatorami) dwoistymi.

Zadania (5.1) — (5.2) i (5.3) — (5.4) nazywamy dwoistymi zadaniami PL. Ponieważ zadania (5.1) — (5.2) i (5.3) — (5.4) zapisany w postaci symetrycznej, ich nazywamy symetrycznymi dwoistymi zadaniami.

Wtedy wzajemnie dwoiste zadania PL mają postać:

Pierwotne zadanie PL max Z = c1*x1 + c2*x2 + ... + cn*xn (5.5) (5.6)

Dualne zadanie PL min f = b1*y1 + b2*y2 + ... + bm*ym (5.7) (5.8)

lub w postaci macierzowej:

Pierwotne zadanie PL max Z = c*x^T A*x^T≤ b x≥ 0

Dualne zadanie PL min f = b^T*y A^T*y^T≥ c y≥ 0

Z modeli (5.5) — (5.6) i (5.7) — (5.8) widać, że, mając matematyczny model dla jednego zadania, możemy łatwo zapisać model zadania dwoistego. Porównując modeli (5.5) — (5.6) i (5.7) — (5.8) zadań dwoistych, możemy zapisać następujące właściwości:

1. Jeśli pierwotne zadanie jest zadanie na maksimum, to wtedy zadanie dwoiste będzie na minimum i odwrotnie, jeśli pierwotne zadanie jest zadanie na minimum, to wtedy zadanie dwoiste będzie na maksimum.

2. Współczynniki с_j funkcji celu pierwotnego zadania będą wolnymi wyrazami dla ograniczeń zadania dwoistego.

3. Wolne wyrazy b_i ograniczeń pierwotnego zadania będą współczynnikami funkcji celu zadania dwoistego.

4. Macierzy ograniczeń zadań pierwotnego i dwoistego to są macierze transponowane.

5. Jeśli pierwotne zadanie jest zadanie maksymalizacji, wtedy układ ograniczeń ma postać nierówności typu „≤”. Dwoiste zadanie będzie rozwiązane na minimum, a ograniczenia przedstawiony w postaci nierówności typu „≥”.

6. Ilość ograniczeń pierwotnego zadania równa się ilości zmiennych zadania dwoistego, a ilość ograniczeń zadania dwoistego równa się ilości zmiennych zadania pierwotnego.

7. Wszystkie zmienne w zadaniach pierwotnym i dwoistym są nieujemne.

ZPL może być też zapisane nie tylko w postaci (5.5) - (5.6), (5.7) - (5.8), również z ograniczeniami mieszanymi w postaci równań i nierówności. Wtedy dwoiste zadanie będzie zapisane:

Pierwotne zadanie PL max Z = (5.9) (5.10)

Dualne zadanie PL min f = (5.11) (5.12)

Zadanie dwoiste z mieszanymi ograniczeniami potrzebuje dodatkowych reguł.

1. Jeśli zmienna х_j zadania pierwotnego jest zmienna nieujemna, wtedy j-ty warunek układu ograniczeń będzie zapisany w postaci nierówności, i odwrotnie.

2. Jeśli zmienna х_j zadania pierwotnego nie jest zmienną nieujemną, wtedy j-te ograniczenie będzie zapisane w postaci równania.

3. Jeśli w zadaniu pierwotnym mamy ograniczenia-równości, wtedy na odpowiednie zmienne zadania dwoistego nie będą nałożone ograniczenia nieujemności.

Oczywiście, że zadanie dwoiste do dwoistego, to jest zadanie pierwotne. Dla tego jest obojętnie, jakie zadanie wziąć za pierwotne, a jakie za dwoiste. Zawsze mówią o parach dwoistych zadań.

5.2. Właściwości dualnych zadań programowania liniowego.

Rozpatrujemy dwoiste zadania PL (5.5) — (5.6) i (5.7) — (5.8).

Twierdzenie 5.1. Dla dowolnych planów dopuszczalnych х= (x₁; x₂; ... ; x_n) i у = (y₁; y₂; ... ; у_m) pierwotnego i dwoistego ZPL będzie spełniona nierówność Z(x) ≤ f(y), to zanaczy

≤
(5.13)

Dowód. Na podstawie nierówności (5.6) i (5.8), mamy

≤
≤

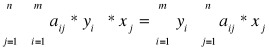
co odpowiada nierówności (5.13). Nierówność (5.13) nazywa się podstawowej nierównością teorii dwoistości.

Treść ekonomiczna nierówności (5.13) polega na tym, że dla dowolnego dopuszczalnego planu produkcji х i dla dowolnego wektora cen у surowców zsumowany zysk od stworzonej produkcji nie przekracza zsumowanych kosztów surowców.

Twierdzenie 5.2. (kryterium optymalności Kantorowicza). Jeżeli dla niektórych dopuszczalnych planów х^* i у^* zadań dwoistych jest spełniona równość Z(х^*)=f(у^*), wtedy х^* i у^* są plany optymalne dla zadań dwoistych.

Dowód. Na podstawie (5.13) dla dowolnego dopuszczalnego planu х zadania pierwotnego i dowolnego dopuszczalnego planu у^* zadania dwoistego spełniona nierówność Z(x) ≤ f(y^*). Ale według treści twierdzenia Z(x^*) = f(y^*). Wtedy na podstawie tranzytywności relacji „≤” i „=”, mamy Z(x) ≤ Z(x^*). Ponieważ х — dowolny plan, wtedy z(x^*) = mах Z, co oznacza, że х^* — jest optymalny plan pierwotnego zadania PL.

Analogiczne udowodnimy, że plan у^* jest optymalnym dla zadania dwoistego.

Sens ekonomiczny twierdzenia 5.2 polega na tym, że plan produkcji х Przedsiębiorstwa 1 i plan cen sprzedaży surowców у Przedsiębiorstwa 2 będą optymalnymi, jeśli dochód od sprzedaży produkcji Przedsiębiorstwa 1 równa się od dochodu od sprzedaży surowców Przedsiębiorstwem 2.

Twierdzenie 5.3. (małe twierdzenie dualności). Dla istnienia optymalnego planu pierwotnego lub dwoistego zadania PL jest konieczne i dostateczne istnienie dopuszczalnego planu dla pierwotnego i dwoistego zadania PL.

Dowód. Konieczność. Niech zadania pierwotne i dwoiste mają optymalne plany х^* i у^*. To oznacza, że max Z(x) = Z(x^*) i min f(y) =f(у^*). Z tego wynika, że х^* i у^* znajdują się w dziedzinie ich planów dopuszczalnych. Odpowiednie układy ograniczeń dla pierwotnego i dwoistego zadania mają rozwiązanie, oni mają co najmniej po jednemu planu dopuszczalnemu (х^* i у^*). Konieczność jest udowodniona.

Dostateczność. Nich każde z dwoistych zadań maje plan dopuszczalny. Udowodnimy, że oni też mają plany optymalne. Niech у^* — dopuszczalny plan zadania (5.7) — (5.8). Wtedy dla dowolnego dopuszczalnego planu х zadania (5.5) — (5.6) na podstawie podstawowej nierówności teorii dwoistości (5.13) otrzymujemy Z(x) ≤ f(y^*). Rozwiązując zadanie (5.5) — (5.6) metodą simplex, mamy ciąg planów oporowych x₀, x₁, ..., dla których funkcje celu Z(x₀), Z(x₁), .... Na podstawie zapisanej wyżej nierówności Z(x) ≤ f(y^*) ten ciąg jest ograniczony z góry. W ciągu zajdzie się największa wartość funkcji celu. Z tego wynika, że istnieje plan dopuszczalny х^*, dla którego Z(x) ≤ Z(x^*).

Analogiczne udowodnimy, że f(y) ≥ f(y^*).

Rozpatrujemy symetryczne zadania dwoiste (5.5) — (5.6) i (5.7) — (5.8). Wprowadzając dodatkowe zmienne x_n+1, x_n+2, ... x_n+m dla zadania pierwotnego i у_m+1, y_m+2, ... , y_m+n dla zadania dwoistego i pamiętając, że max Z = - min (-Z), przeprowadzimy modeli zadań do postaci kanonicznej. Między zmiennymi zadań dwoistych możemy ustalić zależności, przepisując swobodnym zmiennym jednego zadania zmienne bazowe drugiego i odwrotnie:

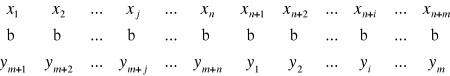
Zmienne występujące w tej samej parze nazywamy zmiennymi dwoistymi (dualnymi) sprzężonymi. Jak widać, zmienna decyzyjna z jednego zagadnienia jest sprzężona z odpowiednią zmienną dodatkową zagadnienia dwoistego (dualnego).

Podajemy bez dowodu

Twierdzenie 5.4 (pierwsze twierdzenie dualności). Jeśli jedno z zadań dwoistych ma optymalne rozwiązanie, wtedy i drugie zadanie ma optymalne rozwiązanie, oraz ekstremalne wartości funkcji celu zadań są równe: Z(x^*) = f(y^*). Jeśli jedno z dwoistych zadań nie maje rozwiązań, ponieważ funkcja celu jest nieograniczona w dziedzinie dopuszczalnych rozwiązań, wtedy układ ograniczeń dla drugiego zadania jest sprzeczny.

Twierdzenie będzie prawidłowe i dla niesymetrycznych zadań dwoistych.

Treść ekonomiczna pierwszego twierdzenia dwoistości polega na tym, że jeżeli zadanie maksymalizacji zysku Przedsiębiorstwa 1 istnieje i rozwiązane, to istnieje i będzie rozwiązanie dwoiste zadanie minimalizacji kosztów zakupu surowców u Przedsiębiorstwa 2. Jednocześnie zysk Przedsiębiorstwa 1 równa się zysku Przedsiębiorstwa 2 (wydatkom na zakupy surowców Przedsiębiorstwem 1) od sprzedaży surowców Przedsiębiorstwu 1. Równości funkcji celu planów zadań dwoistych jest dostatecznie dla optymalności planów dwoistych zadań.

Zagadnieniom dualnym poświęciliśmy sporo miejsca nie tylko ze względu na ciekawe związki, jakie zachodzą między nimi, ale ze względu na możliwości praktycznego ich wykorzystania. Po pierwsze, znając rozwiązanie optymalne jednego z nich, łatwo można podać rozwiązanie optymalne zagadnienia dualnego do rozwiązanego. Z tych względów wygodniej jest czasem rozwiązanie danego zagadnienia PL zastąpić rozwiązaniem zadania dwoistego i dopiero na tej podstawie wyznaczyć rozwiązanie optymalne zadania pierwotnego. Takie postępowanie wskazane jest wtedy, gdy liczba warunków w zadaniu dualnym byłaby znacznie mniejsza od liczby warunków w zadaniu pierwotnym.

Po drugie, znajomość rozwiązania optymalnego zagadnienia dualnego wykorzystuje się do analizy wpływu wyrazów wolnych z warunków ograniczających zadania pierwotnego na optymalną wartość funkcji celu w tym zadaniu. Własność ta dostarcza ciekawej interpretacji zadania dualnego i jego rozwiązania optymalnego, gdy zagadnienie pierwotne ma określoną interpretację ekonomiczną.

Przykład 5.1. Napisać zadanie dualne dla zadania pierwotnego:

przy warunkach ograniczających

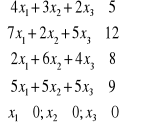
Rozwiązanie. Mame cztere ograniczenia. Dla tego wprowadzimy zmienne
.

Wtedy funkcja celu

i ograniczenia

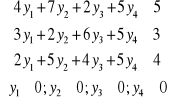
Przykład 5.2. Dla przykładu 4.2 zadania PL rozwiązanego metodą simplex, zapisz zadanie dualne i znajdź optymalny plan zadania dualnego.

Zadanie . Przedsiębiorstwo ma możliwość produkować cztery rodzaje produkcji. W trakcie ich wytwarzania wykorzystuje trzy różne zasoby: sprzęt, surowce, półwyroby. Przedsiębiorstwo dysponuje pierwszym z zasobów w ilości b₁ godzin, drugim - w ilości b₂ kg i trzecim - w ilości b₃ m. Dla produkcji jednej jednostki przemysłowej produkcji rodzaju j (j=1,2,3,4) potrzeba odpowiednio zasobów w ilości: pierwszego - а_1j godzin, drugiego - a_2j kg, trzeciego - a_3j m (j=1,2,3,4). Planowy zysk przedsiębiorstwa w realizacji jednej jednostki produkcji rodzaju j (j=1,4) wynosi с_j pieniężnych jednostek.

b₁=21 b₂=85 b₃=22 a₁₁=0.13 a₁₂=0.21 a₁₃=0.36 a₁₄=0.15 a₂₁=0.31 a₂₂=0.9 a₂₃=1.4 a₂₄=1.26 a_3l=0.37 a₃₂=0.21 a₃₃=0.18 a₃₄=0.12 c_l=7 c₂=9 c₃=4 c₄=8.

Oznaczymy przez х₁, х₂, х₃ , х₄ - ilość jednostek produktów odpowiedniego rodzaju P₁, P₂, P₃, P₄ a przez Z - wartość zysku z realizacji tych produktów.

Matematyczny model zadania pierwotnego:

Z = 7x₁ + 9x₂ + 4x₃+ 8x₄ → max

0.13х₁ + 0.21х₂ + 0.36х₃ + 0.15х₄ <= 21

0.31х₁ + 0.9х₂ + 1.4х₃ + 1.26х₄ <= 85

0.37х₁ + 0.21х₂ + 0.18х₃ + 0.12 х₄ <= 22

x_j
=0, j=1,2,3,4.

Rozwiązanie zadania metodą simplex:

Tabela
х1	х2	х3	х4	х5	х6	х7	bi
0.000	0.000	0.062	-0.110	1.000	-0.188	-0.194	0.747
0.000	1.000	1.725	1.601	0.000	1.381	-1.157	91.937
1.000	0.000	-0.493	-0.585	0.000	-0.784	3.359	7.279
0.000	0.000	8.078	2.320	0.000	6.943	13.102	878.388	= Z

Bazowy plan (0.747, 91.937, 0, 0, 0.747, 0, 0) jest optymalny (х₁ =7.279; х₂ =91.937; х₃ = х₄ = х₆ = х₇.=0; х₅ =0.747), a odpowiednia jemu wartość Z=878.388 celowej funkcji będzie maksymalna.

Matematyczny model zadania dwoistego (dualnego):

Oznaczymy przez y₁, y₂ , y₃ - ceny zasobów Z₁, Z₂, Z₃, z których produkowana produkcja, a przez F - koszty zakupów tych surowców w ilości odpowiednie 21, 85, 22 jednostek (lub sprzedaży tych surowców Przedsiębiorstwem 2).

F = 21y₁ +85y₂ + 22y₃ → min

0.13y₁ + 0.31y₂ + 0.37y₃ >= 7

0.21y₁ + 0.90y₂ + 0.21y₃ >= 9

0.36y₁ + 1.4y₂ + 0.18y₃ >=4

0.15y₁ + 1.26y₂ + 0.12y₃ >= 8

y_j
=0, j=1,2,3.

Ustalimy zależności między zmiennymi zadań dwoistych:

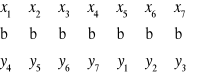
Ponieważ zadanie pierwotne jest rozwiązanie, to istnieje rozwiązanie zadania dwoistego. Mamy na podstawie twierdzeń 5.1-5.3:

1) zmienne х₁ , х₂ , х₅ w zadaniu pierwotnym to są zmienne bazowe, dla tego w zadaniu dualnym odpowiednie zmienne y₄, y₅, y₁ - to są zmienne swobodne, i y₄ = y₅ = y₁ =0.

2) zmienne х₃ , х₄ , х₆, х₇ w zadaniu pierwotnym to są zmienne swobodne, dla tego w zadaniu dualnym odpowiednie zmienne y₆, y₇, y₂ , y₃ - to są zmienne bazowe. Wartości tych zmiennych odczytujemy z wierszu indeksowego Tabeli simplex dla zadania pierwotnego (po transpozycji tej tabeli dla zadania dwoistego wiersz indeksowy występuje jako kolumna wolnych wyrazów). Wtedy y₆=8.078; y₇ = 2.320; y₂ = 6.943; y₃ = 13.102.

Plan sprzedaży surowców Przedsiębiorstwem 2 będzie następujący: pierwszy surowiec nie sprzedajemy (y₁ =0 to jest dla Przedsiębiorstwa 2 nieopłacalne). Lub, z drugiej strony, Przedsiębiorstwo 1 może kupić ten zasób za ceną zerwą.

Dla drugiego i trzeciego surowca ustalimy ceny za jednostkę y₂ = 6.943, y₃ = 13.102.

Wartość F=878.388 celowej funkcji będzie minimalna.

Zmienne dodatkowe y₆=8.078, y₇ = 2.320 wskazują nadwagą cenową w produkcji 3-ej i 4-ej.

Tabela
х1	х2	х3	х4	х5	х6	х7	bi
0.000	0.000	0.062	-0.110	1.000	-0.188	-0.194	0.747
0.000	1.000	1.725	1.601	0.000	1.381	-1.157	91.937
1.000	0.000	-0.493	-0.585	0.000	-0.784	3.359	7.279
0.000	0.000	8.078	2.320	0.000	6.943	13.102	878.388	= Z

5.3. Wykorzystanie estymatorów w analizie rozwiązania zadania programowania liniowego.

Faktycznie w każdym problemie praktycznym sprowadzonym do zagadnienia PL wyznaczenie jego rozwiązania optymalnego nie kończy procesu obliczeniowego. Składa się na to kilka przyczyn. Po pierwsze, skoro optymalizacyjny model liniowy, jest pewnym uproszczonym opisem ilościowym badanego problemu, to otrzymane z niego rozwiązanie optymalne musi być poddane ocenie jego przydatności praktycznej i odpowiednim korektom przed wdrożeniem.

Po drugie, mogą wystąpić w czasie obliczeń pewne zmiany, lub zaistnieje potrzeba uwzględnienia przyszłych zmian w warunkach definiujących model zagadnienia. Mówiąc o zmianach mamy na myśli takie, których efektem będą zmiany wartości pewnych parametrów (składowe wektora wyrazów wolnych, współczynniki w funkcji celu, elementy macierzy współczynników z warunków ograniczających), bądź będą przejawiać się w potrzebie dołączenia do modelu nowych warunków i zmiennych, czy też usunięcia z modelu niektórych warunków i zmiennych,

Nowe warunki w definicji problemu wymagać będą zbudowania nowego modelu i wyznaczenia od początku rozwiązania optymalnego. W wielu przypadkach można do tego celu wykorzystać uzyskane rozwiązanie optymalne wyjściowego zagadnienia PL.

Rozpatrujemy podstawowe twierdzenia analizy dualnych zadań PL.

Twierdzenie 5.5 (drugie twierdzenie dualności). Dla tego, żeby plany х^* i y^* zadań dwoistych byli optymalnymi, jest koniecznie i dostatecznie spełnienie warunków:

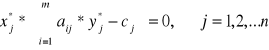
(5.14)

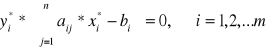
(5.15)

Dowód. Konieczność. Niech х^* i у^* — plany optymalne dla pierwotnego i dwoistego zadania PL

Zadanie pierwotne max Z = (5.16) (5.17)

Zadanie dualne min f = (5.18) (5.19)

Na podstawie twierdzenia 5.4 dla tych planów wartości funkcji celu równa się: Z(x^*)=f(y^*), to znaczy

=
(5.20)

Zapisując w wyrażeniu (5.20) wolne wyrazy b_i z równości (5.17), otrzymujemy

=
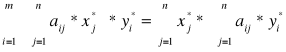
, i wtedy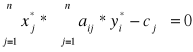
.

Ponieważ
wtedy z ostatniej równości mamy warunek (5.14). Analogiczne można udowodnić warunki (5.15).

Dostateczność. Niech dla niektórych dopuszczalnych planów х^* i y^* są spełnione warunki (5.14). Udowodnimy ich optymalność. Po sumowaniu równości (5.14) według wszystkich j od 1 do n i spełniając przekształcenia odwrotne do wyżej zapisanych, otrzymujemy wzór (5.20). Na podstawie Twierdzenia 5.2 plany х^* i y^* są optymalne.

Twierdzenie jest prawidłowe dla dowolnej pary zadań dwoistych.

Z warunków (5.14), (5.15) wynika: jeśli jakiekolwiek ograniczenie jednego z zadań dualnych jest optymalnym, w planie występuje w postaci dokładnej nierówności, to odpowiednia zmienna optymalnego planu dwoistego zadania powinna równać się zero; jeśli jakakolwiek zmienna jednego zadania jest dodatnia, wtedy odpowiednie ograniczenie zadania dualnego dla planu optymalnego powinno być równością.

Takim czynem, jeśli
wtedy y_i^* = 0; jeśli y_i^* > 0, wtedy
.

Analogicznie, jeśli
wtedy x_j^* = 0; jeśli x_j^* > 0, wtedy
.

Ekonomicznie to oznacza, że jeśli dla niektórego optymalnego planu х^* produkcji wykorzystanie i-go surowcu jest dokładnie mniejsze od jego zapasu b_i, wtedy w optymalnym planie zadania dualnego odpowiednia zmienna równa się zero. Jeśli w niektórym planie optymalnym zmienna i-ta jest większa od zero, wtedy w dualnym zadaniu odpowiednia zmienna równa się zero, co oznacza całkowite wykorzystanie odpowiedniego surowca dla produkcji. Z tego wynika, że zmienne dwoiste mogą występować miarą deficytu zasobów. Zasób jest deficytny (całkowicie wykorzystywany w optymalnym planie produkcji) ma dodatnią zmienną dualną, zasób zbędny (wykorzystywany nie całkowicie) ma zerową zmienną dualną.

Rozpatrujemy zadanie optymalizacji produkcji przedsiębiorstwa. Przepuścimy, że ilości zasobów mogą zmieniać się. Powstaje pytanie: w jakie sposób te zmiany wpływają na zysk przedsiębiorstwa od sprzedaży produkcji? Na to pytanie odpowiada twierdzenie (bez dowodu).

Twierdzenie 5.6 (trzecie twierdzenie dualności - twierdzenie o ocenach). Zmienne dualne pokazują przyrost funkcji celu, który jest spowodowany małymi zmianami wolnego wyrazu odpowiedniego ograniczenia pierwotnego zadania PL, mianowicie

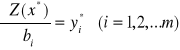
(5.21)

Wyjaśnimy sens ekonomiczny Twierdzenia 5.6. Dla tego w równości (5.21) zamienimy cząstkowe pochodne przyrostami. Wtedy
. Jeżeli b_i = 1 i b_k = 0, k=1,2,...m, k≠i wtedy
. To oznacza, że zmienna dwoista liczbowo równa się przyrostu funkcji celu przy wzrostu wolnego wyrazu odpowiedniego ograniczenia na jedynką.

W naszych przykładach ograniczymy się do najprostszego przypadku analizy poopty-malizacyjnej: do badania stabilności otrzymanego rozwiązania optymalnego względem zmieniających się wartości jednego ze współczynników funkcji celu albo składowej wektora wyrazów wolnych.

Badanie stabilności rozwiązania optymalnego ze względu na zmieniający się współczynnik funkcji celu ma ustalić zakres zmienności jego wartości, który zapewnia wybór danego rozwiązania optymalnego.

Można udowodnić, że wartość wybranego współczynnika c_j może wpływać na wartości wskaźników optymalności rozwiązania bazowego, natomiast nie wyznacza wartości jego zmiennych bazowych. Stad wybór rozwiązania x* jako rozwiązania optymalnego utrzymany będzie tak długo, jak długo wszystkie jego wskaźniki z_j - c_j będą ustalonego znaku. Rozróżniamy przy tym dwa przypadki:

1) Współczynnik c_j dotyczy zmiennej niebazowej x_j w rozwiązaniu optymalnym x*. Od współczynnika c_j zależy jedynie wskaźnik optymalności zmiennej x_j. Rozwiązanie x* pozostanie rozwiązaniem optymalnym ze względu na maksymalizację funkcji celu przy tych wartościach c_j, które zapewniają

czyli dla

2) Współczynnik c_j dotyczy zmiennej bazowej x_j rozwiązania optymalnego x*. Wtedy c_j może oddziaływać na wartości wskaźników optymalności a_ij wszystkich zmiennych nie-bazowych, ponieważ jest on składową wektora c. Rozwiązanie x* pozostanie optymalne dla tych c_j które zapewniają

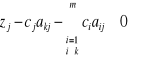
gdzie k jest numerem równania, w którym występuje zmienna bazowa x_jt .

Przejdziemy do ustalania wpływu zmian wartości składowych b_j - wektora wyrazów wolnych na stabilność uzyskanego rozwiązania optymalnego x*. Zmiany te nie mogą wpływać na wartości wskaźników optymalności a_ij rozwiązania, będą zaś wpływały na wartości zmiennych bazowych tego rozwiązania.

Niech zmieniającą swą wartość będzie składowa k wektora b. Zapiszemy

gdzie
jest wartością początkową, przy której wyznaczono rozwiązanie x*. Zmiany
mają być takie, aby

,

czyli, aby

,

gdzie
jest wektorem jednostkowym z jedynką jako składową o numerze k, macierz
w tablicy sirnpleksowej wyznaczają te same kolumny, które w pierwszej tablicy tworzyły macierz jednostkową.

Z tego wynika, że mówiąc o stabilności rozwiązania optymalnego x* przy zmieniającym się wyrazie wolnym mamy na myśli nie to, że nie ulegną zmianie wartości składowych rozwiązania x*, lecz to, że nie ulegnie zmianie jego zestaw zmiennych bazowych i będą one nieujemne.

Niech
oznacza kolumnę k w macierzy
. Z ostatniej nierówności mamy więc

,

co odpowiada układowi nierówności

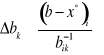
gdy
,

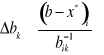
gdy
,

dla i = 1, ..., m.

Rozwiązanie tego układu nierówności wyznaczy taki zakres zmienności na przyrost
będący przedziałem który zapewnia niezmienioną strukturę zmiennych bazowych rozwiązania optymalnego.

Przykład 5.3. Wykorzystując rozwiązanie zadania PL podanego wyżej ustalić stabilność podanego rozwiązania optymalnego ze względu na zmienności a) współczynnika c₂ b) współczynnika c₃ c) współczynnika b₃.

a) W rozwiązaniu zmienna x₂ jest zmienną bazową. Aby ustalić szukany zakres zmienności c₂ musimy rozwiązać układ nierówności

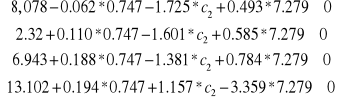
Wtedy

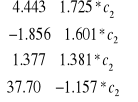
, po przekształceniach i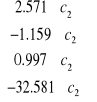
,

z czego wynika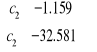
.

Tabela
х1	X2	х3	х4	х5	х6	х7	bi
0.000	0.000	0.062	-0.110	1.000	-0.188	-0.194	0.747
0.000	1.000	1.725	1.601	0.000	1.381	-1.157	91.937
1.000	0.000	-0.493	-0.585	0.000	-0.784	3.359	7.279
0.000	0.000	8.078	2.320	0.000	6.943	13.102	878.388	=Zmax

Wnioskujemy, że rozwiązanie ZPL będzie stabilne pod warunkiem, że
. Jeżeli współczynnik
ma sens ceny i
, wtedy, oczywiście, ZPL będzie niestabilne.

b) Współczynnik c₃ dotyczy zmiennej swobodnej x₃, dla tego aby wyznaczyć szukany zakres zmienności c₃ wystarczy rozwiązać nierówność

czyli

.

To jest warunek stabilności ZPL pod względem zmienności współczynnika c_3.

c) Tablica wyznacza rozwiązanie optymalne zadania PL. W kolumnach pod x₅, x₆, x₇ mamy podaną macierz
. Mamy zatem

;
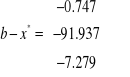
, a stąd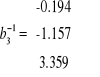
.

Dostajemy układ nierówności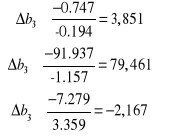

który wyznacza obszar zmienności przyrostu

Ponieważ pierwotne wartości macierzy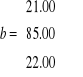
, wtedy
, czyli
- zakres zmienności na współczynnik
będący przedziałem który zapewnia niezmienioną strukturę zmiennych bazowych rozwiązania optymalnego.

5

Lekcja 5. Dualność zadań programowania liniowego. Wykorzystanie estymatorów w analizie rozwiązania zadania programowania liniowego.

---