Cel ćwiczenia

• Wyznaczenie stałej siatki dyfrakcyjnej.

.Wzory

Stałą siatki dyfrakcyjnej d nazywamy odległość między środkami sąsiednich szczelin. Do jej obliczenia korzystamy z przekształconego wzoru na maksimum interferencyjne:

Wzór na kąt ugięcia α:

Wzór na wartość sinα kąta ugięcia:

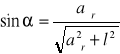
Rysunek

λ =626,2[nm]

Obliczenia:

I siatka

Szczelina zerowa = Sinα₀= λ/l

l=20[cm]

sinα₀=31,31[cm]

α_śr=(8,5+8,5)/2

α_śr=8,5[cm]

kąt ugięcia α

tgα=0,425[^o]

wartość sinα kąta ugięcia

sinα=0,39[^o]

wartość d stałej siatki dyfrakcyjnej

d=1605,64[μm]

Rząd widma	Długość fali	Odległość prążka		Odległość średnia	Odległość siatki	Stała siatki dyfrakcyjnej	Wartość średnia
k	λ	a1	a2	aśr	l	d	dśr
1	632,8 nm	8,5	8,5	8,5mm	20 mm	1605,64μm	3305,597μm

II siatka

Szczelina zerowa = Sinα₀= λ/l

l=30[cm]

sinα₀=20,87[cm]

α_śr=(12,5+12,5)/2

α_śr=12,5[cm]

kąt ugięcia α

tgα=0,42[^o]

wartość sinα kąta ugięcia

sinα=0,385[^o]

wartość d stałej siatki dyfrakcyjnej

d=3252,99[μm]

Rząd widma	Długość fali	Odległość prążka		Odległość średnia	Odległość siatki	Stała siatki dyfrakcyjnej	Wartość średnia
k	λ	a1	a2	aśr	l	d	dśr
1	632,8 nm	12,5	12,5	12,5mm	30 mm	3252,99 μm	3305,597μm

III siatka

Szczelina zerowa = Sinα₀= λ/l

l=35[cm]

sinα₀=17,89[cm]

α_śr=(14+14)/2

α_śr=14[cm]

kąt ugięcia α

tgα=0,4[^o]

wartość sinα kąta ugięcia

sinα=0,3714[^o]

wartość d stałej siatki dyfrakcyjnej

d=5058,16[μm]

Rząd widma	Długość fali	Odległość prążka		Odległość średnia	Odległość siatki	Stała siatki dyfrakcyjnej	Wartość średnia
k	λ	a1	a2	aśr	l	d	dśr
1	632,8 nm	14	14	14 mm	35 mm	5058,16 μm	3305,597μm

Błąd stałej siatki dyfrakcyjnej:

d_śr=3305,597[μm]

tgα_śr=0,415[^o]

sinα_0śr=23,37[cm]

sinα_śr=0,3821[^o]

∆d_I=0,0002[μm]

∆d_II=0,0001 [μm]

∆d_III=0,0001[μm]

∆ tgα_I=0,01[^o]

∆ tgα_II=0,005[^o]

∆ tgα_III=0,015[^o]

∆ sinα_0I=7,94[cm]

∆ sinα_0II=2,5[cm]

∆ sinα_0III=5,48[cm]

∆ sinα_I=0,0079[^o]

∆ sinα_II=0,0029[^o]

∆ sinα_III=0,0107[^o]

∆l_I=0,2[cm]

∆l_II=0,3[cm]

∆l_III=0,35[cm]

Wnioski

Układ równoległych i równo oddalonych od siebie szczelin, przepuszczających światło, nazywamy siatką dyfrakcyjną. Szczeliny na siatce można otrzymywać nacinając diamentem na płytce szklanej szereg rys. Rysy te są nieprzezroczyste dla światła. Światło przechodzi przez gładką powierzchnię między rysami. Odległość między środkami sąsiednich szczelin nazywamy stałą siatki dyfrakcyjnej. W ćwiczeniu udało nam się dokonać wyznaczenia siatki dyfrakcyjnej za pomocą naniesienia punktów na kartkę.

2