Wydział AEiI, kierunek AiR

Ćwiczenia laboratoryjne z fizyki:

Wyznaczanie stałej siatki dyfrakcyjnej, pomiar długości światła laserowego, wyznaczanie szerokości szczeliny.

Grupa V, sekcja IV

Tomasz Bartoszek

Bartłomiej Romanowski

Gliwice, 20/04/1999

1. Wiadomości ogólne.

Dyfrakcja światła polega na tym, że gdy natrafia ono na przeszkody porównywalne z długością fali albo przechodzi przez niewielkie otwory lub szczeliny wówczas występuje wyraźne odchylenie od prostoliniowości rozchodzenia się światła, co ujawnia się w wystąpieniu charakterystycznego rozmycia granicy cienia i światła i w pojawieniu się ciemnych i jasnych (lub też barwnych) prążków na granicy cienia. Wyjaśnienie zjawiska ugięcia na podstawie falowej teorii światła podał Fresnel. Oparł się on przy tym na znanej już dawniej zasadzie Huyghensa, według której każdy element czoła fali może być uważany za nowe źródło fal. Zjawiska uginania się światła dzielimy według sposobu ich obserwacji na ugięcia Fresnela (gdy odległości między przeszkodą a ekranem lub przeszkodą a źródłem światła są skończone) i ugięcia Fraunhofera (gdy obie odległości są nieskończone).

Spośród ugięć typu Fraunhofera, tj. przy użyciu wiązek równoległych światła, szczególnie ważną rolę odgrywa ugięcie przez szczelinę, a zwłaszcza przez tzw. siatki dyfrakcyjne, stanowiące układy równoległych do siebie szczelin, rozmieszczonych w równych odstępach. Siatki dyfrakcyjne wykonuje się na błonach fotograficznych stosując dyfrakcję światła laserowego. Jedne z miejsc naświetlonych stanowią zasłony (te ciemne), inne stanowią szczeliny (te jasne, przepuszczające).

Promienie ugięte na siatce mogą nakładać się, czyli interferować ze sobą, gdyż są promieniami spójnymi, to znaczy że różnice faz między nimi zależą tylko od różnicy dróg geometrycznych, nie zależą od czasu. Maksima dyfrakcyjne wystąpią wtedy, gdy różnica faz będzie równa 2kπ

Wzajemne wygaszenie fal wystąpi, gdy:

2. Krótki opis przebiegu doświadczenia.

W ćwiczeniu obserwowaliśmy dyfrakcję światła na siatce dyfrakcyjnej oraz na pojedynczej szczelinie.

Wyznaczanie stałej siatki dyfrakcyjnej

• Sprawdzono poprawność ustawienia spektrometru.

• Siatkę dyfrakcyjną umieszczono na stoliku obrotowym spektrometru. Płaszczyzna siatki powinna być prostopadła do osi przyrządu.

• Obracając lunetką z okularem (względem osi przyrządu) doprowadzano do pokrycia linii krzyża pomiarowego z kolejnymi prążkami dyfrakcyjnymi. Notowano kąty ugięcia dla trzech rzędów (na lewo i prawo od prążka zerowego). Pomiary powtarzano pięciokrotnie.

Pomiar długości światła laserowego.

• Siatkę dyfrakcyjną ustawiono na stoliku, prostopadle do kierunku padania światła.

• Zmierzono odległość siatki dyfrakcyjnej od ekranu.

• Notowano położenia kolejnych jasnych prążków dyfrakcyjnych dla trzech rzędów na lewo i prawo od prążka zerowego.

Wyznaczanie szerokości szczeliny.

• Szczelinę umieszczono na stoliku na osi zestawu, prostopadle do kierunku padania światła laserowego.

• Dobrano szerokość szczeliny tak, aby na listwie pomiarowej uzyskać wyraźne prążki dyfrakcyjne z odstępem ok. 1 mm

• Suport powinien znajdować się w skrajnym położeniu. Aby uzyskać pełny obraz dyfrakcyjny, prążek centralny powinien być przesunięty w stosunku do szczeliny fotorezystora o ok. 10-12 mm.

• Ustalono zakres miernika na 2 mA, ustalono opcje programu i włączamy przesuw detektora.

• Obliczono średnie wartości kątów ugięcia dla poszczególnych rzędów.

• Obliczono stałą siatki dyfrakcyjnej ze wzoru:

3. Obliczenia i analiza błędów.

Do obliczeń przyjęto następujące wartości błędów:

• Błąd pomiaru kąta ugięcia prążka Δα= 0^o20'

• Błąd odczytu rozmieszczenia prążków dyfrakcyjnych Δx_n= 5 [mm].

• Błąd odczytu odległości między siatką dyfrakcyjną a ekranem Δl= 10 [mm].

Obliczono kąty ugięcia poszczególnych prążków ze wzoru na średnią arytmetyczną. Otrzymano następujące wyniki:

lp.	n=1	n=2	n=3
1	6°15'	13°00'	20°15'
2	6°30'	13°00'	20°00'
3	6°30'	12°57'	19°54'
4	6°20'	12°57'	19°57'
5	6°09'	12°57'	19°57'

Obliczono średnią wartość kątów n_1,2,3. Wartości te użyto do dalszych obliczeń. Otrzymano następujące wartości:

n=1 α₁=6°20'

n=2 α₂=12°58'

n=3 α₁=20°00'

Obliczamy stałą siatki dyfrakcyjnej i jej błąd ze wzorów:

Otrzymano następujące wyniki:

n=1 d₁=5342,1*10^-9 [m] Δd=154,0*10^-9 [m]

n=2 d₂=5252,6*10^-9 [m] Δd=13,3*10^-9 [m]

n=3 d₁=5169,0*10^-9 [m] Δd=62,0*10^-9 [m]

Średnią wartość stałej siatki d i jej błąd obliczono ze wzoru na średnią ważoną:

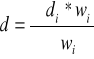
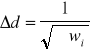
Otrzymano: d=5249,6*10^-9 [m] Δd=13,0*10^-9 [m]

Obliczono długość światła laserowego ze wzoru:

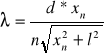
gdzie: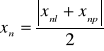

d - wartość stałej siatki dyfrakcyjnej obliczonej wcześniej

Błąd  obliczono metodą różniczki zupełnej:

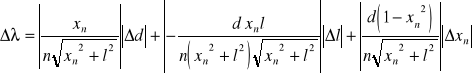
[m],

gdzie: xn=0,001[m], l=0,001[m].

Otrzymano następujące wyniki:

λ₁= 702,3*10^-9 [m] Δλ₁= 25,4*10^-9 [m]

λ₂= 698,9*10^-9 [m] Δλ₂= 4,2*10^-9 [m]

λ₃= 699,7*10^-9 [m] Δλ₃= 3,2*10^-9 [m]

Ostatecznie wartość długości światła laserowego i jej błąd obliczamy ze wzoru na średnią ważoną:

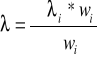
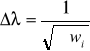
Otrzymano następujący wynik:

λ=699,4*10^-9 [m] Δλ=2,5*10^-9 [m]

Następnie obliczono szerokość szczeliny ze wzoru:

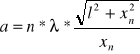
gdzie:

 - długością światła laserowego obliczona wcześniej,

l = 0,50[m] jest odległością detektora od szczeliny,

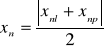
Odległość szczeliny od detektora l = 0,50 m

Położenie prążka centralnego x₀ = 12,6 mm

n	xn [mm]
	lewo	prawo
1	1,8	2,0
2	3,7	3,8
3	5,7	5,7

Błąd wyliczenia szerokości szczeliny a obliczono metodą różniczki zupełnej:

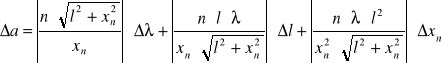
Otrzymano następujące wyniki:

a₁=184,1*10^-6 [m] Δa=10,5*10^-6[m]

a₂=186,5*10^-6 [m] Δa=7,5*10^-6[m]

a₃=184,1*10^-6 [m] Δa=6,4*10^-6[m]

Średnią wartość szerokości szczeliny i jej błąd obliczono ze wzoru na średnią ważoną:

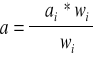
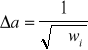
Otrzymano następujący wynik:

a=184,9*10^-6 [m] Δa=4,4*10^-6 [m]

4. Podsumowanie.

Ostatecznie otrzymano następujące wyniki liczonych wartości:

stała siatki dyfrakcyjnej d=(5249,6±13,0)*10^-9 [m]

długość fali światła lasera λ=(699,4±2,5)*10^-9 [m]

szerokość szczeliny a=(184,9±4,4)*10^-6 [m]

W doświadczeniu obserwowaliśmy zjawisko dyfrakcji świtała, które mogło zajść jedynie w wypadku napotkania przez falę świetlną przeszkody o porównywalnych rozmiarach z długością fali. Otrzymane wyniki również mają porównywalne wartości i na tej podstawie możemy sądzić, że są prawidłowe.

---