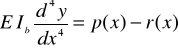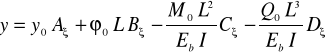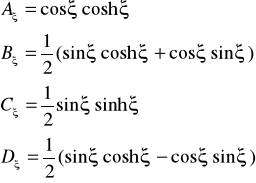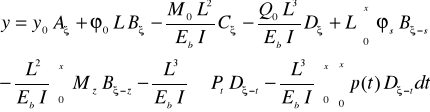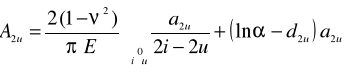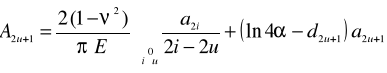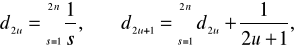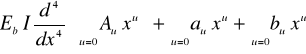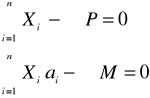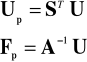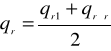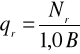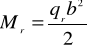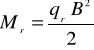4. ŁAWY FUNDAMENTOWE

 ławy fundamentowe (fundamenty taśmowe) - ustroje belkowe spoczywające na podłożu gruntowym pod ścianami lub rzędami słupów

4.1. RODAJE ŁAW

 klasyfikacja ze względu na rodzaj materiału

ŁAWY FUNDAMENTOWE

1

KAMIENNE

2

CEGLANE

3

BETONOWE

4

ŻELBETOWE



murowane z kamienia



murowane z cegły

a

MONO-LITYCZ-NE

a

MONO-LITYCZNE

b

PREFA-BRYKO-WANE

b

PREFA-BRYKOWANE

 klasyfikacja ze względu na rodzaj materiału

		ŁAWA FUNDAMENTOWA O PRZEKROJU
1)	PROSTOKĄTNYM			2)	SCHODKOWYM		3)	TRAPEZOWYM

 klasyfikacja ze względu na rodzaj obciążenia

		ŁAWA FUNDAMENTOWA OBCIĄŻONA
1	OSIOWO			2	MIMOŚRODOWO
					w 1 płaszczyźnie

4.2. OBLICZNIE ŁAW FUNDAMENTOWYCH

 obejmuje

4.2.1. OBLICZNIE ODDZIAŁYWAŃ

 obejmuje wielkości charakterystycznych (osiadania, odporu) i sił wewnętrznych (momentów zginających i sił tnących) dla przyjętego schematu współdziałania układu „ława fundamentowa - podłoże gruntowe”

 założenia

1)	ława jest liniowo-sprężystym ustrojem prętowym (belką),
2)	podłoże jest liniowo-odkształcalnym masywem gruntowym (zwykle półprzestrzenią, półpłaszczyzną lub warstwą sprężystą jednorodną lub uwarstwioną poziomo),

 metody analizy układu „ława - podłoże”

METODY ROZWIĄZANIA

1

ANALITYCZNE

2

NUMERYCZNE

A

ŁAWA FUNDAMENTOWA NA PODŁOŻU WINKLERA

A

ŁAWA NA PODŁOŻU ŚWITKI-MURAWSKIEGO (LISOWSKIEGO)

 

układ sprężyn na nieodkształcalnym podłożu, Bleich, Umanski, Hetenyia,



układ sprężyn na nieodkształcalnym podłożu z membraną (uwzględniający odrywania) rozwiązywany metodą różnic skończonych,

B

ŁAWA FUNDAMENTOWA NA KLASYCZNEJ PÓŁPRZESTRZENI SPRĘŻYSTEJ

B

ŁAWA FUNDAMENTOWA NA KLASYCZNEJ PÓŁ-PRZESTRZENI ROZWIĄZY-WANA KOMBINOWANĄ METODĄ SIŁ I ODKSZTAŁCEŃ

 

rozwiązywana metodą szeregów potęgowych, Gorbunow-Posadow,

 

Żemoczkin, Król (dowolnie uwarstwiona),

C

ŁAWA NA PODŁOŻU WŁASOWA

B

ŁAWA FUNDAMENTOWA NA KLASYCZNEJ PÓŁ-PRZESTRZENI ROZWIĄZY-WANA KOMBINACJĄ METOD MES i MKEB



Cheung,

 ograniczenie do ław o skończonej długości nieodkształcalnych w kierunku poprzecznym,

4.2.1.1. ŁAWA NA PODŁOŻU WINKLERA (ROZWIĄZYWANA METODĄ ELEMENTÓW BRZEGOWYCH)

 podłoże modeluje układ pionowych sprężyn ustawionych pionowo na nieodkształcalnej poziomej podstawie,

 model podłoża Winklera - charakteryzuje sprężysta zależność postaci

(4.1)

w której: r(x) - reakcja (odpór) podłoża,

y(x) - osiadanie podłoża,

C - współczynnik sztywności (podatności) podłoża,

 idea rozwiązania:

1)	uwzględnia się w równaniu różniczkowym osi ugiętej belki reakcję podłoża (4.2) w którym: Eb - moduł sprężystości belki, Ib - moment bezwładności przekroju belki, p(x) - obciążenie ciągłe ławy,
2)	wyznacza się rozwiązanie równania (4.2) w postaci relacji (4.3) gdzie: y0, 0, M0, Q0, - wartości geometryczne i statyczne na lewym końcu belki (parametry brzegowe dla x=0), A, B, C, D, - funkcje wyrażone wzorami (4.4)  - stosunek współrzędnej x do długości L,
3)	uogólnienie rozwiązania (4.3) na przypadki dowolnego układu przegubów (o kącie obrotu s) i obciążeń zewnętrznych w postaci skupionych sił Pt, momentów Mz i obciążenia rozłożonego p(t) (4.5) gdzie: A, B, C, D, - funkcje analogiczne do (4.4), uwzględniające współrzędne położenia (s, z, t), mierzone względem lewego końca belki.

4.2.1.2. ŁAWA NA KLASYCZNEJ PÓŁPRZESTRZENI (ROZWIĄZYWANA METODĄ ELEMENTÓW BRZEGOWYCH WG KONCEPCJI GORBUNOWA-POSADOWA)

 idea rozwiązania

1)	przyjmuje się, że ugięcie y(x) spoczywającej na podłożu belki oraz przemieszczenie pionowe podłoża w(x), opisane szeregami potęgowymi (4.6) są jednakowe tzn. (4.7)
2)	opisuje się reakcję podłoża r(x) i obciążenie zewnętrzne p(x) za pomocą wzorów (4.8)
3)	uwzględnia się w równaniu różniczkowym osi ugiętej belki (4.9) powyższe zależności, co po rozwiązaniu daje wyrażenia na współczynniki Au: a) parzyste (4.10) a) nieparzyste (4.11) w których:  - stosunek długości belki L do jej szerokości B, d2u, d2u+1 - współczynniki wg wzorów (4.12) E,  - moduł odkształcenia i współczynnik Poissona dla gruntu Podłoża,
4)	wyznacza się z końcowego równania (4.13) p nieznane parametry au poprzez ich porównanie ze znanymi parametrami bu, prowadzącego do układu równań (skończonego dla skończonej liczby wyrazów szeregu),

 wyniki zebrane są w postaci tablic i nomogramów, z których określa się wartości osiadań, odporu i sił wewnętrznych

4.2.1.3. ŁAWA NA SPRĘŻYSTEJ PÓŁPRZESTRZENI (ROZWIĄZYWANA METODĄ ŻEMOCZKINA)

 obciążenie stanowi zestaw pionowych sił skupionych rozmieszczonych w regularnych odstępach,

 idea rozwiązania:

1)	rzeczywistą ławę zastępuje się belką wspornikowo utwierdzoną w jednym końcu, spoczywającą na zestawie regularnie rozmieszczonych wahaczy, opartych o podłoże
2)	buduje się kanoniczny układ równań metody sił, przyjmując za niewiadome n sił Xi w wahaczach i uwzględniając nieznane przemieszczenie yo oraz obrót o w utwierdzeniu (4.14) w którym: δki - przemieszczenie w punkcie k od obciążenia Xi=1, uwzględniające osiadanie podłoża wki i ugięcie belki yki (4.15) ki - przemieszczenie w punkcie k od obciążenia Xi=1 wywołane obciążeniem zewnętrznym, yo, o - przemieszczenie i kąt obrotu w miejscu utwierdzenia belki, ak - odległość punktu k od utwierdzenia,
3)	uzupełnia się układ (4.14) dwoma równaniami równowagi (sumy sił pionowych i sumy momentów) różniczkowym osi ugiętej belki (4.16)
4)	wyznacza się z układu (4.14)-(4.16) niewiadome Xi, yo, o (a następnie - osiadanie i odpór gruntu, oraz siły wewnętrzne).

4.2.1.4. ŁAWA NA SPRĘŻYSTEJ PÓŁPRZESTRZENI (ROZWIĄZYWANA METODĄ CHEUNGA)

 idea postępowania:

1)	dzieli się ławę na dwuwęzłowe prętowe elementy skończone, natomiast powierzchnię brzegową podłoża pod nią na prostokątne elementy brzegowe (stykające się środkami z odpowiednimi węzłami belki),
2)	B tworzy się macierzowy układ równań (4.17) w którym: R - to wektor obciążenia w węzłach belki, U - wektor poszukiwanych przemieszczeń węzłów, Kb - globalna macierz sztywności układu „ława - podłoże”, K - macierz sztywności belki, A - macierz podatności podłoża,
3)	wyznacza się przemieszczenia belki U z równania (4.17), a osiadania podłoża Up i reakcje Fp z zależności (4.18)

4.2.2. SPRAWDZENIE I I II STANU GRANICZNEGO

 zgodnie z zasadami podanymi dla żelbetowych stóp fundamentowych,

4.2.3. WYMIAROWANIE ŁAW FUNDAMENTOWYCH

 obejmuje sprawdzenie warunku ze względu na

		SPRAWDZENIE WARUNKU ZE WZGLĘDU NA
1	ZGINANIE			2	ŚCINANIE
	dla stóp żelbetowych warunek ustalający rozkład i ilość zbrojenia

4.2.3.1. SPRAWDZENIE ŻELBETOWYCH ŁAW FUNDAMENTOWYCH ZE WZGLĘDU NA ZGINANIE

 założenia

1)	obciążenie wypadkowe pozostaje w rdzeniu przekroju,
2)	obciążenie wypadkowe działa mimośrodowo w 1 płaszczyźnie,
3)	uwzględnia się (lub pomija) ciężar własny ławy i gruntu spoczywającego na niej,
4)	obciążenie stanowi najniekorzystniejszy zestaw obciążeń (wartości obliczeniowych).

 zbrojenie ławy stanowi zestaw prętów umieszczonych nad dolną podstawą prostopadle do jej osi),

 zasada obliczeń - dzieli się jednakowej długości fragment na 2 wsporniki utwierdzone pod środkiem muru (słupa), a obciążone uśrednionym odporem gruntu i wyznacza niekorzystniejszy moment utwierdzenia (dla którego projektuje się zbrojenie),

 tok postępowania

1)	oblicza się rozkład oddziaływania podłoża na 2 trapezy
a) b)	w przypadku obciążenia mimośrodowego (4.19) w przypadku obciążenia osiowego (4.20) gdzie: qr, qrśr - oddziaływanie obliczeniowego obciążenia: maksymalne i pod środkiem muru, B - szerokość ławy,
2)	wyznacza się obliczeniową wartość momentu utwierdzenia
a)	w przypadku obciążenia mimośrodowego (4.21)
b)	w przypadku obciążenia osiowego (4.22) b - „wysięg” niekorzystniejszego wspornika,
3)	określa się ilość zbrojenia
	- zgodnie z punktem (3.a) z punktu 3.2.5.1.1. wykładu

 zalecenia co do grubości otulenia, rozstawu i średnicy prętów, klasy stali i betonu - zgodnie z punktu 3.2.5.1.1. wykładu,

4.2.3.2. SPRAWDZENIE ŻELBETOWYCH ŁAW FUNDAMENTOWYCH ZE WZGLĘDU NA ŚCINANIE

 założenia - identyczne jak w punkcie 4.2.3.1,

 sprawdzenie - zgodnie z ogólnymi zasadami sprawdzania ścinania,

4.2.3.3. SPRAWDZENIE ŻELBETOWYCH ŁAW FUNDAMENTOWYCH ZE WZGLĘDU NA PRZEBICIE

 założenia - identyczne jak w punkcie 4.2.3.1,

 sprawdzenie - zgodnie z ogólnymi zasadami sprawdzania przebicia i docisku,

5. RUSZTY FUNDAMENTOWE

 fundamenty rusztowe stosowane są gdy:

1)	pola utworzone przez siatkę słupów zbliżone są do kwadratów, a zastosowanie ław tylko w jednym kierunku prowadzi do nadmiernych ich szerokości,
2)	elementy przenoszące obciążenie budowli na fundamenty ułożone są wzdłuż krzyżujących się wzajemnie kierunków

 ruszt fundamentowy - tworzy ortogonalny (promienisto-koncentryczny) układ ław spoczywających na podłożu, a obciążonych w miejscach ich połączeń (węzłach),

 rodzaje rusztów fundamentowych

		RUSZTY FUNDAMENTOWE Z WĘZŁAMI
1	SZTYWNYMI			2	PRZEGUBOWYMI
	uwzględniające skręcanie belek				nie uwzględniające skręcania belek

 metody obliczania oddziaływań i sił wewnętrznych w rusztach

METODY ROZWIĄZYWANIA (NUMERYCZNE)

1

RUSZT FUNDAMENTOWY NA PODŁOŻU WINKLERA

2

RUSZT FUNDAMENTOWY NA PODŁOŻU SPRĘŻYSTYM

a

METODA ODKSZTAŁCEŃ

a

KOMBINOWANĄ METODĄ SIŁ I ODKSZTAŁCEŃ



Król

b

METODA SZTYWNYCH ELEMENTÓW SKOŃCZONYCH

b

KOMBINACJĄ METOD MES i MKEB



Cheung

 I i II stan graniczny sprawdza się zgodnie z PN, natomiast konstrukcję projektuje się stosownie do reguł kształtowania żelbetowych belek

6. PŁYTY FUNDAMENTOWE

 płyty fundamentowe - przenoszą obciążenie z budowli na całą powierzchnię podłoża zawartą w ich obrysie,

 rodzaje rusztów fundamentowych

1) klasyfikacja ze względu na sztywność

		PŁYTY FUNDAMENTOWE
1	SZTYWNE			2	ODKSZTAŁCALNE (SPRĘŻYSTE)
	zachowują się jak sztywny blok

2) klasyfikacja ze względu na konstrukcję

		PŁYTY FUNDAMENTOWE
1)	PŁYTA CIĄGŁA (O STAŁEJ GRUBOŚCI)			2)	PŁYTA WZMOCNIONA ŻEBRAMI (UKŁAD PŁYTOWO- ZĘBROWY)					3)	PŁYTA W POSTACI ODWRÓCONE-GO STROPU GRZYBKOWEGO
4)	PŁYTA W POSTACI ODWRÓCONEGO SKLEPIENIA						5)	PŁYTA W POSTACI ODWRÓCONEJ POWŁOKI

 metody obliczania oddziaływań i sił wewnętrznych w płytach (schematy obliczeniowe)

SCHEMATY OBLICZENIOWE PŁYT FUNDAMENTOWYCH

1

UPROSZCZONE

2

DOKŁADNE



obciążone odporem podłoża (np. równomiernym)

A

PŁYTA NA PODŁOŻU WINKLERA

B

PŁYTA NA PODŁOŻU WŁASOWA

C

PŁYTA NA PÓŁPRZESTRZENI SPRĘŻYSTEJ



rozwiązywana metodą szeregów potęgowych (Gorbunow-Posadow)

 I i II stan graniczny sprawdza się zgodnie z PN, natomiast konstrukcję projektuje się stosownie do reguł kształtowania odpowiednich ustrojów żelbetowych

7. SKRZYNIE FUNDAMENTOWE

 skrzynie fundamentowe - stosuje się przy dużych obciążeniach (pod budynki wysokościowe lub wieżowe) gdy wymagana jest pełna sztywność fundamentu i w miarę równomierne jego obciążenie,

 budowa skrzyni fundamentowej

 schematy obliczeniowe

		SCHEMAT OBLICZENIOWY SKRZYNI FUNDAMENTOWEJ
1	CAŁKOWICIE SZTYWNY UKLAD PŁYTOWY NA PÓŁPRZESTRZENI SPRĘŻYSTEJ			2	CIENKOŚCIENNA KONSTRUKCJA SPOCZYWAJĄCA NA SPRĘZYSTEJ PÓŁPRZESTRZENI
	na który działa od góry rozłożone powierzchniowo obciążenie,				wg teorii Własowa,
	tworzy dla ustalenia reakcji podłoża - przepony oblicza się jako tarcze,				tworzy w przekroju poprzecznym zamkniętą ramę na sprężystym podłożu,

 I i II stan graniczny sprawdza się zgodnie z PN, natomiast konstrukcję projektuje się stosownie do reguł kształtowania odpowiednich ustrojów żelbetowych

---