Regresja krzywoliniowa

Regresja krzywoliniowa - jednakowym przyrostom zmiennej niezależnej towarzyszą różne co do wielkości lub też różne co do wielkości i kierunku zmiany zmiennej zależnej.

A. Funkcja potęgowa

Transformacja funkcji na postać liniową:

układ równań normalnych:

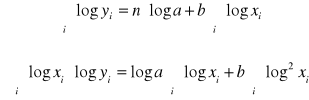
stąd

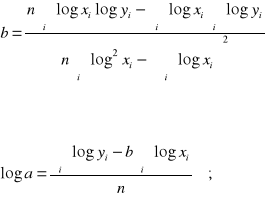
Parametr b jest interpretowany jako współczynnik elastyczności, tzn. jeżeli zmienna X wzrośnie o 1%, to Y zmieni się średnio o b procent.

B. Funkcja wykładnicza

Transformacja do postaci liniowej:

Układ równań normalnych:

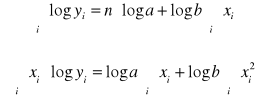
stąd

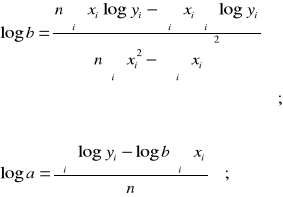
Parametr b funkcji wykładniczej jest interpretowany jako średni przyrost względny, tzw. stopa przyrostu. Jeżeli X wzrośnie o jednostkę, to Y zmieni się średnio o (b-1)100 procent.

C. Funkcja hiperboliczna

Układ równań:

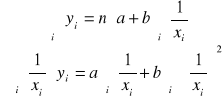
stąd

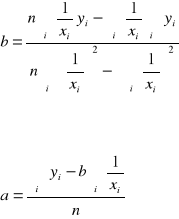
Parametr a interpretujemy jako współczynnik nasycenia. Jeżeli X rośnie, to Y utrzymuje się przeciętnie na poziomie a.

D. Funkcja kwadratowa (parabola)

Rozwiązujemy układ trzech równań:

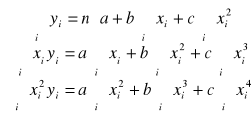
metodą wyznacznikową uzyskamy:

Parametrów tej funkcji nie interpretuje się.

OCENA DOBROCI DOPASOWANIA FUNKCJI REGRESJI DO DANYCh EMPIRYCZNYCH.

Odchylenie standardowe składnika resztowego:

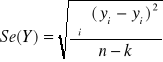
ukazuje średnią różnicę pomiędzy zaobserwowanymi wartościami zmiennej Y i krzywą regresji.

Współczynnik zbieżności (indeterminacji):

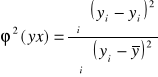
informuje, jaka część zmienności Y nie została wyjaśniona wpływem X określonym aproksymowaną funkcją.

Współczynnik determinacji:

R²(yx) = 1 - ²(yx)

pokazuje, jaka część zmienności Y została wyjaśniona oddziaływaniem X określonym funkcją regresji.

Indeks korelacji:

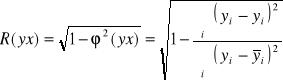
jest miarą korelacji krzywoliniowej. Współczynnik ten przyjmuje wartości z przedziału 0;1, a zatem pokazuje siłę skorelowania zmiennej zależnej Y ze zmienną niezależną X, nie informując o kierunku korelacji.

PRZYKŁAD 1

Obliczanie parametrów krzywoliniowych funkcji regresji opisujących wpływ wielkości produkcji w tys. sztuk (x_i) na wysokość kosztów jednostkowych w zł (y_i), (źródło: dane umowne):

Wielkość produkcji	xi	1	2	3	4	5
Wysokość kosztów j.	yi	73	56	40	34	32

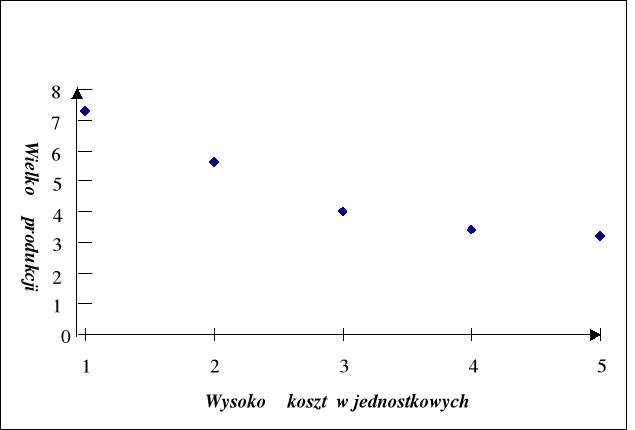
Rys. 1.. Wykres korelacyjny wysokości kosztów jednostkowych względem wielkości produkcji

1. Aproksymujemy funkcję potęgową
   .

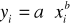
Funkcję przekształcamy w postać liniową:
,

xi	yi	log xi	log yi	log^2 xi	log xi log yi
1	73	0,0000	1,8633	0,0000	0,0000
2	56	0,3010	1,7482	0,0906	0,5263
3	40	0,4771	1,6021	0,2276	0,7644
4	34	0,6021	1,5315	0,3625	0,9221
5	32	0,6990	1,5051	0,4886	1,0520
x	x	2,0792	8,2502	1,1693	3,2648

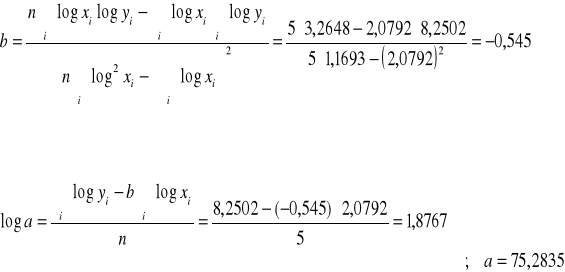
log
= 1,8767 - 0,545 log x_i,

a po zdelogarytmowaniu

,

co oznacza, że jeżeli wielkość produkcji wzrośnie o 1%, to koszty jednostkowe zmaleją o 0.545%.

dopasowanie funkcji:

xi	yi
1	73	75,3	-2,3	5,29	26	676
2	56	51,4	4,6	21,16	9	81
3	40	41,2	-1,2	1,44	-7	49
4	34	35,1	-1,1	1,21	-13	169
5	32	31,1	0,9	0,81	-15	225
15	235	x	x	29,91	0	1200

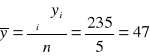
Odchylenie standardowe składnika resztowego:

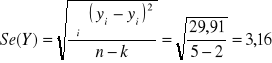
Współczynnik zbieżności:

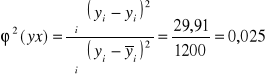
B. Aproksymujemy funkcję wykładniczą
.

Funkcję przekształcamy w postać liniową:

,

xi	yi	log yi	xi^2	xi log yi
1	73	1,8633	1	1,8633
2	56	1,7482	4	3,4864
3	40	1,6021	9	4,8063
4	34	1,5315	16	6,1260
5	32	1,5051	25	7,5255
x	x	8,2502	55	23,8175

,

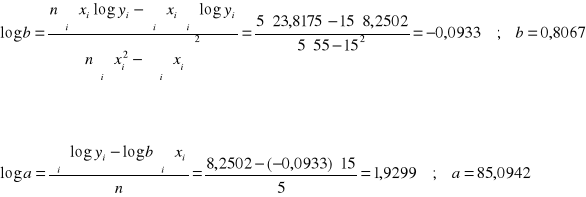
a po zdelogarytmowaniu

.

co oznacza, że jeżeli wielkość produkcji wzrośnie o 1 sztukę, to koszty jednostkowe zmaleją średnio o 19%.

dopasowanie funkcji

xi	yi
1	73	68,9	4,1	16,81
2	56	55,8	0,2	0,04
3	40	45,2	-5,2	27,04
4	34	36,6	-2,6	6,76
5	32	29,7	2,3	5,29
15	235	x	x	55,94

Odchylenie standardowe składnika resztowego:

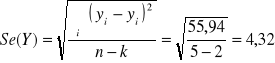
Współczynnik zbieżności:

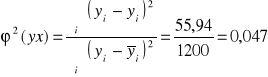
C. Aproksymujemy funkcję hiperboliczną
.

Wykonujemy obliczenia pomocnicze

xi	yi	1/ xi	yi ⋅ 1/xi	(1/xi)^2
1	73	1,00	73,0	1,000
2	56	0,50	28,0	0,250
3	40	0,33	13,2	0,109
4	34	0,25	8,5	0,063
5	32	0,20	6,4	0,040
x	235	2,28	129,1	1,462

Obliczamy parametry funkcji:

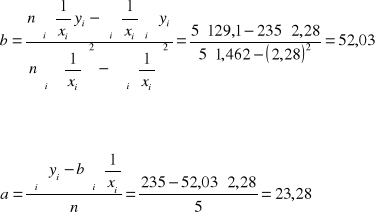
Funkcja ma postać

co oznacza, że jeżeli wielkość produkcji rośnie, to koszty jednostkowe będą utrzymywały się przeciętnie na poziomie 23,28 zł.

dopasowanie funkcji

xi	yi
1	73	75,3	-2,3	5,29
2	56	49,3	6,7	44,89
3	40	40,6	-0,6	0,36
4	34	36,3	-2,3	5,29
5	32	33,7	-1,7	2,89
15	235	235,2	x	58,72

Odchylenie standardowe składnika resztowego:

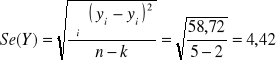
Współczynnik zbieżności:

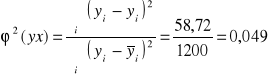
Porównując odchylenia składnika resztowego oraz współczynniki zbieżności obliczone dla trzech aproksymowanych funkcji, stwierdzamy, że najlepiej zależność między wielkością produkcji a wysokością kosztów jednostkowych określa funkcja potęgowa. Dopasowanie funkcji jest najlepsze (
)

Współczynnik determinacji

wskazuje, że zmienność wysokości kosztów jednostkowych w prawie 97,5% jest objaśniana zmiennością wielkości produkcji,

a współczynnik korelacji

r(yx) = - 0,987

informuje, że mamy do czynienia z bardzo silną korelacją ujemną, co oznacza że im większa skala produkcji tym niższe koszty jednostkowe wytworzenia produktu.

12

---