Akademia Techniczno-Humanistyczna w Bielsku-Białej
Wydział: Nauk o Materiałach i Środowisku
Kierunek:
Ćwiczenie 80
Temat: Wyznaczanie długości fali świetlnej za pomocą spektrometru siatkowego.
Hiniuial
Część teoretyczna:
Długość fali λ
Jest to odległość między dwoma najbliższymi punktami zgodnymi w fazie, tzn. takimi, których odchylenia od stanu równowagi są w każdej chwili jednakowe.
Długość fali wyznaczamy ze wzoru:
gdzie: λ - długość fali
c - stała siatki
- kąt ugięcia
k - rząd widma
Dyspersja światła D
Rozszczepienie barwnego światła polegające na zachowaniu różnej wartości współczynnika załamania światła w zależności od jego różnej częstości drgań.
Dyspersje wyznaczamy ze wzoru:
gdzie: D - dyspersja kątowa siatki
k - rząd widma
c - stała siatki
α - kąt ugięcia
Ugięcie światła (dyfrakcja )
Uginanie fali na przeszkodzie, której rozmiary są porównywalne z długością tej fali. Zjawisko dyfrakcji światła można zaobserwować, gdy wiązka światła przechodzi przez siatkę dyfrakcyjną, którą jest płytka szklana zarysowana równoległymi liniami w ilości co najmniej kilkaset na 1mm . Ugięte promienie światła interferują ze sobą i w zależności od tego, czy spotykają się w fazach zgodnych, czy przeciwnych, na ekranie za siatką pojawiają się jasne i ciemne prążki. Jasny prążek pośrodku ekranu nazywany jest zerowym, po obu jego stronach są prążki pierwszego rzędu, za nimi prążki drugiego rzędu itd.
Siatka dyfrakcyjna
Płaska płytka szklana o równej grubości, posiadająca szereg równoległych rys w odstępach ok. 0,5 μ. Rysy płytki odgrywają rolę zasłon, natomiast przerwy między nimi rolę szczelin. Jeżeli na siatkę pada prostopadle wiązka promieni jednobarwnych, o długości fali λ, to każda jej szczelina staje się źródłem nowych fal elementarnych
(zasada Huygensa - Fresnela ).
Widmo
Jest to zespół barw otrzymanych w wyniku rozszczepienia światła białego. Rozróżniamy widma emisyjne, powstające przy promieniowaniu substancji oraz widma absorpcyjne , powstające wskutek pochłaniania przez określone substancje części przechodzącego przez nie promieniowania białego.
Do badania widm używa się spektrometru
Interferencja
Nakładanie się fal, przy czym zgodnie z zasadą superpozycji wychylenie fali wypadkowej jest sumą algebraiczną wychyleń fal składowych. W wyniku interferencji fale mogą się wzmacniać ( jeżeli spotkają się w odpowiednich fazach ) lub wygaszać (jeśli spotkają się w fazach przeciwnych ).
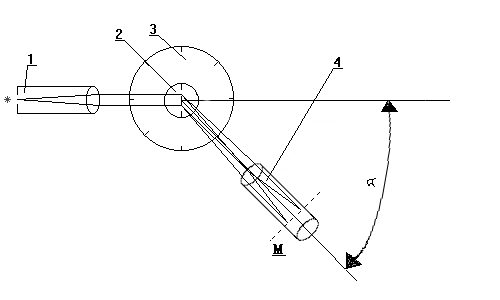
Rysunek do doświadczenia
Rysunek przedstawia spektrometr siatkowy.
Na rysunku znajdują się elementy (odpowiednio):
Kolimator
Przesuwna ramka z trzema siatkami dyfrakcyjnymi różnych wartościach stałej siatki
N=100; c =
N=400; c =
N=600; c =
Stolik, zaopatrzony w skalę kątową
Lunetka
α - kąt ugięcia
M - płaszczyzna ogniskowej obiektywu
Przyrządy potrzebne do przeprowadzenia doświadczenia
Spektrometr siatkowy, statyw z rurką Pluckera, transformator wysokiego napięcia, zasilacz.
B. Pomiary i obliczenia:
Tab. 1: Wyniki pomiarów i obliczeń:
k |
α |
Δα |
λ |
Δλ |
D |
ΔD |
||||
|
(˚) |
(′) |
rad |
(˚) |
(′) |
rad |
nm |
nm |
mm-1 |
mm-1 |
1 |
3 |
19.5 |
0.0580 |
0 |
10.2 |
0.0030 |
580 |
3 |
100.2 |
1.3 |
2 |
6 |
46.98 |
0.11839 |
0 |
2 |
0.00058 |
590.54 |
0.29 |
201 |
5 |
3 |
10 |
16.56 |
0.1793 |
0 |
5.5 |
0.0016 |
594.58 |
0.52 |
304 |
12 |
4 |
13 |
46.98 |
0.24056 |
0 |
9 |
0.0026 |
595.61 |
0.64 |
411 |
23 |
5 |
17 |
30 |
0.3054 |
0 |
12 |
0.0035 |
601.41 |
0.67 |
524 |
33 |
No = 100 mm-1; d= 10 μm; |
||||||||||
Tab. 2: Wyniki pomiarów i obliczeń:
Barwa prążka |
|
Δ |
λ |
Δλ |
Λt |
Δ* |
||||
|
(˚) |
(') |
rad |
(˚) |
(') |
rad |
nm |
nm |
nm |
% |
Fioletowa |
16 |
28.5 |
0.2875 |
0 |
3.5 |
0.001 |
472.8 |
1.6 |
483 |
2.1 |
Zielono-morksa |
17 |
49.98 |
0.3112 |
0 |
4 |
0.0012 |
510.5 |
1.9 |
534 |
4.4 |
Żółta |
20 |
46.02 |
0.36245 |
0 |
3 |
0.00087 |
591.1 |
1.4 |
595 |
0.6 |
Pomarańczowa |
21 |
1.98 |
0.3671 |
0 |
4 |
0.0012 |
598.3 |
1.8 |
614 |
2.6 |
Czerwona 1 |
22 |
10.98 |
0.3872 |
0 |
8 |
0.0023 |
629.4 |
3.6 |
640 |
1.7 |
Czerwona 2 |
23 |
31.5 |
0.41059 |
0 |
2.5 |
0.00073 |
665.4 |
1.1 |
725 |
8.2 |
No=600 mm-1 d=1/600μm k=1 *w oparciu o H.Szydłowski: „ Pracownia fizyczna” |
||||||||||
1. Obliczenie średniej wielkości konta:
a. wzór ogólny
![]()
![]()
- średnia wielkość kąta
![]()
a- wielkość kąta uzyskana przy pierwszym pomiarze
![]()
b- wielkość kąta uzyskana przy drugim pomiarze
b. obliczenia
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2. Obliczenie błędu bezwzględnego średniej wielkości kąta:
a. wzór ogólny
![]()
Δ![]()
- wielkość błędu względnego średniej wielkości kąta
![]()
a- wielkość kąta uzyskana przy pierwszym pomiarze
![]()
b- wielkość kąta uzyskana przy drugim pomiarze
b. obliczenia
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3. Obliczenie długości fali:
a. wzór ogólny
![]()
λ - długość fali
d - stała siatki (d=1/No)
k - rząd ugięcia (rząd widma)
![]()
- kąt ugięcia
b. obliczenia
![]()
![]()
![]()
![]()
![]()
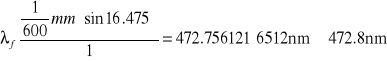
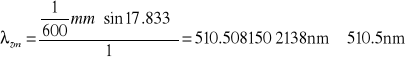
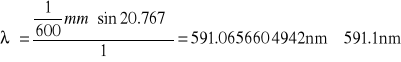
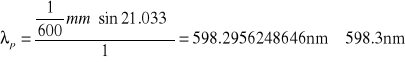
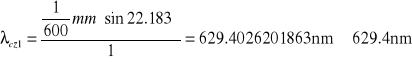
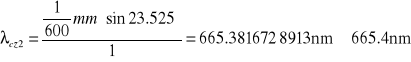
4. Obliczenie wartości dyspersji siatki D:
a. wzór ogólny
![]()
D - wartość dyspersji siatki
k - rząd ugięcia
d - stała siatki
![]()
- kąt ugięcia
b. obliczenia
![]()
![]()
![]()
![]()
![]()
5. Obliczenie błędu bezwzględnego długości fali Δλ:
a. wzór ogólny
![]()
Δλ - błąd bezwzględny długości fali λ
Δ![]()
- błąd bezwzględny średniej wielkości kąta w radianach
![]()
- średnia wielkość kąta
λ - długość fali
b. obliczenia
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. Obliczenie błędu bezwzględnego wartości dyspersji siatki ΔD:
a. wzór ogólny:
![]()
ΔD - błąd bezwzględny wartości dyspersji siatki
Δ![]()
- błąd bezwzględny średniej wielkości kąta ugięcia podany w radianach
![]()
- kąt ugięcia
![]()
- błąd względny stałej siatki
b. obliczenia
![]()
![]()
![]()
![]()
![]()
Obliczenie względnego odchylenia od wartości tablicowych:
a. wzór ogólny:
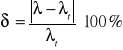
![]()
- odchylenie od wartości tablicowych
λ - długość fali wynikająca z obliczeń
λt - długość fali dla zaobserwowanych linii widma neonu odczytana z tablic (H.Szydłowski: „ Pracownia fizyczna”)
b. obliczenia
![]()
![]()
![]()
![]()
![]()
![]()
C. Wnioski:
Metoda ta wykazuje wysoką skuteczność. Nie zgodności z wynikami tablicowymi są niewielkie i wynikają z błędów pomiarowych. Ich przyczyny to:
- Słaba widoczność prążków, zwłaszcza w przypadku prążka czerwonego II
- Trudność z interpretacją słownych określeń koloru prążka, co powodowało zmierzenie położenia prążka o niewłaściwej barwie
Są to błędy nie sprawiające trudności w wyeliminowaniu podczas kolejnych pomiarów, co przemawia dodatkowo za skutecznością tej metody.
Bibliografia:
H.Szydłowski: „ Pracownia fizyczna”, Państwowe Wydawnictwo Naukowe, Warszawa 1973
1
Wyszukiwarka
Podobne podstrony:
Wyznaczanie długości fali świetlnej za pomocą spektrometru (, ?WICZENIE NR 4
Ćw 85-Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej”, Szkoła, Fizyka
Wyznaczanie długości fali świetlnej za pomocą pierścieni Newtona., Study =], FIZYKA, fizyka laborki
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej, Wrocław, dn. 16.11.94
sprawka fizyka, Wyznaczanie długości fali świetlnej za pomocą pierścieni Newtona., nr
Ćw 85 Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Sprawozdanie 305 - Wyznaczanie długości fali świetlnej za pomocą pierścieni Newtona, Fizyka
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej 3 DOC
Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej
Lab 24, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siatk
więcej podobnych podstron