Rozdział 19

Elementy teorii relacyjnych baz danych

W rozdziale prezentujemy materiał dotyczący matematycznych podstaw relacyjnego modelu danych. Z uwagi na charakter książki nie jest to opis kompletny.

Relacyjny model baz danych stworzony został przez E.F. Codda w roku 1970.

Termin "relacyjna baza danych" oznacza bazę zbudowaną z relacji. Po przeczytaniu poprzednich dwóch rozdziałów, w których koncentrowaliśmy się na opisie tabel, Czytelnik zadaje sobie pewnie pytanie, co wspólnego ma tabela z relacją?

Relacja to abstrakcyjny termin matematyki (którego definicję podajemy poniżej), natomiast tabela jest konkretną reprezentacją relacji. Wynika z tego, że jedna relacja może być odwzorowana za pomocą wielu różnych tabel. W modelu relacyjnym przyjmuje się, że:

• kolejność wierszy i kolumn w tabelach jest nieistotna (to, że dane Krzysia przechowywane są w czwartym wierszu tabeli Uczeń, jak i to, że wiersz zawierający informacje o imionach rodziców poprzedza wiersz z danymi o telefonie kontaktowym nie ma żadnego znaczenia dla SZBD)

• wiersze zawierające takie same dane są identyczne.

Natomiast w tabeli przedstawiającej konkretny przypadek relacji identyczne dane przechowywane będą w różnych wierszach.

Do zdefiniowania terminu relacja potrzebne nam będą dwie podstawowe definicje:

Def.1 Schematem relacji nazywamy zbiór R = {A₁,A₂,....A_n};

gdzie: A₁,A₂,....A_n są atrybutami (reprezentowanymi poprzez nazwy kolumn).

Tabela Uczeń, opisywana w poprzednim rozdziale, jest przykładem schematu relacji Uczeń = {ID ucznia, Imię, Nazwisko, Adres, Imiona rodziców, Telefon kontaktowy}

Każdemu atrybutowi A przyporządkowany jest zbiór dopuszczalnych wartości (odpowiada mu typ zmiennych). Na przykład dziedzinami atrybutów w przypadku tabeli Ocena są:

Dom (ID ucznia) = TEKST (5)

Dom (Ocena) = LICZBA (1,1)

Dom (Zdobyta za) = TEKST (50)

Dom (ID przedmiotu) = TEKST (5)

Def.2 Dziedziną relacji o schemacie R = {A₁,A₂,....A_n} nazywamy sumę dziedzin wszystkich jej atrybutów Dom (R) = Dom (A₁)  Dom (A₂)    Dom (A_n).

Tak więc dziedziną relacji odwzorowanej na tabeli Ocena będzie suma dziedzin wszystkich jej atrybutów: Dom (ID ucznia)  Dom (Ocena)  Dom (Zdobyta za)  Dom (ID przedmiotu).

Def. 3 Relacja o schemacie R = {A₁,A₂,....A_n} jest to skończony zbiór r = {t₁,t₂,....t_m} odwzorowań t_i : R Dom (R) takich, że dla każdego j z zakresu 1<=j<=n, zachodzi zależność: t_i(A_j) Dom (A_j).

Pojedyncze odwzorowanie nosi nazwę krotki i odpowiada mu pojedynczy wiersz tabeli. Przykładem krotki będzie następujący wiersz pochodzący z tabeli Uczeń:

JBA

Jaś

Badura

Bytom 33-333, ul.Pawła 2/12

Olek, Grażyna

501-50150112

Kolejnym, niezbędnym dla zrozumienia teorii relacyjnych baz danych terminem, jest Klucz. Do zdefiniowania tego terminu konieczne jest wprowadzenie jeszcze dwóch definicji:

Def. 4 Ograniczeniem krotki t relacji r o schemacie R do zbioru atrybutów X  R nazywamy odwzorowanie będące ograniczeniem krotki t do zbioru atrybutów X, t_IX: X Dom (X)

Na przykład, ograniczeniem krotki z poprzedniego przykładu do zbioru atrybutów X = {ID ucznia, Imię, Nazwisko} będzie krotka:

JBA

Jaś

Badura

Def. 5 Relacja r o schemacie R = {A₁,A₂,....A_n} spełnia zależność funkcyjną X Y (X,Y  R), jeżeli dla każdych dwóch krotek t,u r zachodzi warunek: jeśli t_IX = u_IX to t_IY = u_IY

To znaczy, że o spełnieniu przez pewną relację zależności funkcyjnej postaci X Y możemy mówić wtedy, jeżeli w ramach krotek tej relacji wartości atrybutów zbioru X jednoznacznie determinują wartości atrybutów zbioru Y.

Dla relacji przedstawionej za pomocą tabeli Uczeń możemy wskazać następujący zbiór spełniających ją zależności funkcyjnych:

ID ucznia {Imię, Nazwisko, Adres, Imiona rodziców, telefon kontaktowy}

{Imię, Nazwisko} {ID ucznia, Adres, Imiona rodziców, telefon kontaktowy}

{telefon kontaktowy, Imię} {ID ucznia, Nazwisko, Adres, Imiona rodziców}

Przyjrzyjmy się po kolei każdej z wymienionych zależności funkcyjnych.

Ponieważ pole ID ucznia dodaliśmy do bazy Dziennik właśnie po to, aby móc zawsze jednoznacznie określić, którego z uczniów opisują dane atrybuty (takie jak ocena z poszczególnych przedmiotów, Nr szafki, czy Imiona rodziców) możemy być pewni, że wartość tego atrybutu jednoznacznie określa wartości wszystkich pozostałych atrybutów tabeli. Innymi słowy, wartość JBA wskazuje na Jasia Badurę, jego dane personalne , oceny i szafkę w szatni.

Kombinacja imienia i nazwiska ucznia również pozwala nam jednoznacznie określić, o którego z uczniów "chodzi". Jednak, w przeciwieństwie od poprzedniej zależności funkcyjnej, ta jest spełniana w danym momencie, tzn. dla aktualnie przechowywanych w bazie danych. Po dopisaniu do bazy nowego ucznia o identycznym imieniu i nazwisku jak imię i nazwisko ucznia już w bazie zarejestrowanego, nie będziemy mogli na podstawie imienia i nazwiska jednoznacznie określić pozostałych atrybutów ucznia.

Za pomocą kombinacji imienia i numeru telefonu możemy jednoznacznie zidentyfikować ucznia w bazie. Z dość dużym prawdopodobieństwem moglibyśmy wykorzystywać tę kombinację nie tylko dla aktualnie wprowadzonych danych, ale również w przyszłości — prawdopodobieństwo, że do szkoły zostanie przyjęty uczeń o takim samym imieniu i z takim samym numerem telefonu kontaktowego jest raczej niewielkie (o ile wykluczyć przypadek rodzeństwa, któremu rodzice dla wygody nadali takie same imiona). Jednak w praktyce staramy się znaleźć i wykorzystać jako klucz zależność funkcyjną o najmniejszym z możliwych zakresie zbioru X.

Def. 6 Nadkluczem relacji r o schemacie R = {A₁,A₂,....A_n} nazywamy dowolny zbiór atrybutów X  R taki, że zachodzi zależność funkcyjna X R. Innymi słowy, o nadkluczu mówimy w przypadku, gdy wartość każdego atrybutu jest jednoznacznie zdeterminowana przez wartość atrybutów zbioru X. Jednym z nadkluczy jest zawsze zbiór wszystkich atrybutów R.

Def. 7 Kluczem relacji r o schemacie R = {A₁,A₂,....A_n} nazywamy każdy minimalny nadklucz, tzn. taki nadklucz, który nie zawiera w sobie żadnego nadklucza. Tak więc zbiór atrybutów X jest kluczem, jeżeli wartość każdego atrybutu w R jest jednoznacznie zdeterminowana przez wartość atrybutów zbioru X i żaden z podzbiorów zbioru X nie posiada już tej własności. Dla każdej relacji można wskazać co najmniej jeden klucz, przy czym najczęściej jest ich więcej.

Spróbujmy znaleźć klucze relacji odwzorowanej na tabelę Uczeń:

Na mocy def. 7 nadkluczem tej relacji jest zbiór X₁ = {ID ucznia, Imię, Nazwisko, Adres, Imiona rodziców, telefon kontaktowy}. Ponieważ podzbiór zbioru X₂ ={ID ucznia, Imię, Nazwisko} również jest nadkluczem tej relacji, zbiór X₁, na mocy def. 7 nie jest kluczem relacji Uczeń. Z tego samego powodu zbiór X₂, również nie jest kluczem relacji. Minimalnym nadkluczem, do jakiego doprowadzi nas te rozumowanie to zbiór X₃ = {ID ucznia}. I jest to jeden z poszukiwanych kluczy relacji. Kolejnym kluczem jest zbiór X₄ = {telefon kontaktowy, Imię}. Znalezienie następnych kluczy pozostawiamy Czytelnikowi.

Spośród wszystkich kluczy relacji wyróżnia się jeden (nazywany kluczem głównym lub kluczem podstawowym) w odróżnieniu od kluczy kandydujących. Atrybuty wchodzące w skład klucza głównego z reguły zaznacza się przez ich podkreślenie. Dla relacji Uczeń wybraliśmy na klucz główny klucz ID ucznia. Efektem powyższych ustaleń jest następujący zapis relacji:

Uczeń = {ID ucznia, Imię, Nazwisko, Adres, Imiona rodziców, telefon kontaktowy}

W rozdziale przedstawiliśmy, w sposób nieco bardziej formalny, informacje zawarte w rozdziałach 17 i 18. Na tak zdefiniowanych relacjach możliwe jest dokonywanie kilku przekształceń. Praktyczne podejście do przekształceń dokonywanych na danych przedstawione zostanie w rozdziale następnym. Osoby, które będą miały pewne trudności z materiałem przedstawionym poniżej powinny najpierw przestudiować rozdział 20, a po jego lekturze jeszcze raz spróbować wrócić do drugiej części bieżącego rozdziału.

Operatory relacyjnych baz danych

Pierwszy typ przekształceń, które można wykonywać na relacjach , wynika z definicji relacji jako pewnego zbioru. Doskonale Czytelnikowi znanym operatorom algebry zbiorów, czyli   , odpowiadają operatory UNION (suma relacji), INTERSEC (cześć wspólna relacji, przecięcie, przekrój relacji) i MINUS (dopełnienie relacji, różnica relacji).

Na sumę dwóch relacji rs składają się wszystkie elementy relacji r i wszystkie elementy relacji s. Wynikiem przecięcia relacji rs jest relacja składająca się z elementów wspólnych relacji r i s. Wynikiem odjęcia relacji rs jest relacja powstała w wyniku usunięcia z relacji r wszystkich elementów wchodzących w skład relacji s.

Dodatkowo, dla operacji na relacjach zdefiniowane są następujące operatory: selekcji, projekcji, iloczynu kartezjańskiego i złączenia naturalnego. Poniżej podajemy ich definicje.

Def. 8 Selekcją relacji r o schemacie R = {A₁,A₂,....A_n} nazywamy zbiór tych krotek relacji r , w których wartością atrybutu A jest element a, przy założeniu, że AR , a Dom(A), co zapisujemy σ_Aa(r) = {tr / t(A)=a}, oraz, dla dowolnego warunku logicznego F, zbiór krotek relacji r spełniających warunek F, co zapisujemy σ_F(r) = {tr / t spełnia warunek F}

Tak więc: σ _{NAZWISKO=JANOWSKA}(Uczeń) = {t}; gdzie t jest następującą krotką:

t(ID ucznia)= MJA, t(Imię)= Małgosia,

t(Adres)= Gliwice 35-212, ul. Paśki 3b,

t(Imiona rodziców)= Marcin, Magda, t(Telefon kontaktowy)= 299-717-921

Dla operatora selekcji prawdziwe są następujące twierdzenia:

T1. σ_F(rs) = σ_F(r)  σ_F(s); selekcja sumy relacji równa jest sumie selekcji

T2. σ_F(rs) = σ_F(r)  σ_F(s); selekcja przecięcia relacji równa jest przecięciu selekcji

T3. σ_F(rs) = σ_F(r)  σ_F(s); selekcja różnicy relacji równa jest różnicy selekcji.

Na podstawie twierdzeń T1 — T3 możemy w dowolny sposób zmieniać kolejność operacji teoriomnogościowych względem selekcji. Zmiana kolejności operacji nie wpłynie na jej wynik.

Def. 9 Projekcją relacji r na zbiór atrybutów XR nazywamy zbiór ograniczeń do atrybutów zbioru X wszystkich krotek relacji r, co zapisujemy  _X(r) = {t_IX: tr}

Tak więc:  _{Imie, Nazwisko}(Nauczyciel)= {Maurycy, Polak; Zdybek, Sęk; Michał, Pasek}

Dla operatora projekcji prawdziwe są następujące twierdzenia:

T4. _X(_Y(r)) =  _X(r) przy założeniu, że XY

T5. _X((rs) =  _X(r)   _X(s); projekcja sumy relacji równa jest sumie projekcji

T6. σ_F( _X(r)) =  _X(σ_F (r)); selekcja projekcji równa jest projekcji selekcji

Na przykład:

 _Imię ( _{Imię, Nazwisko}(Nauczyciel) =  _Imię (Nauczyciel) = {Maurycy, Zdybek, Michał}

Na podstawie twierdzeń T4, T5 możemy w dowolny sposób zmieniać kolejność operacji sumy i selekcji względem projekcji. Zmiana kolejności operacji nie wpłynie na jej wynik.

Def.10 Iloczynem kartezjańskim dwóch relacji r o schemacie R = {A₁,A₂,....A_n} i s o schemacie S = {B₁,B₂,....B_n}, przy założeniu RS=0, nazywamy relację q=rs o schemacie Q = {A₁,A₂,....A_n, B₁,B₂,....B_n} składającą się z wszystkich krotek tq dla których istnieją krotki ur i vs takie, że: t(A_i )= u(A_i ) dla 1<=i<=n oraz t(B_i )= v(B_i ) dla 1<=i<=m.

Mówiąc nieco prościej — iloczyn kartezjański relacji r i s jest zbiorem wszystkich możliwych połączeń krotek obu relacji.

Takie połączenie tabel w ogromnej większości przypadków nie ma najmniejszego sensu. Proszę natomiast zauważyć, że połączenie takie tabeli Uczeń z tabelą Ocena, w wyniku którego otrzymamy tylko te kombinacje wartości, dla których krotka ID ucznia ma tę samą wartość jest niezwykle przydatne.

Def.11 Złączeniem naturalnym relacji r o schemacie R = {A₁,A₂,....A_n} i s o schemacie S = {B₁,B₂,....B_n} jest relacja q o schemacie Q = RS taka, że q={t:  ur i vs takie, że u_IR=t i v_IS=t}

Tak więc złączeniem naturalnym relacji jest zbiór wszystkich możliwych połączeń krotek relacji, przy których ich wspólne atrybuty mają takie same wartości.

Dla operatora złączenia naturalnego prawdziwe są następujące twierdzenia:

T7. qq=q; wynikiem złączenia relacji z samą sobą jest dana relacja

T8. qr = rq; naprzemienność złączenia

T9. (qr) s = q(rs); przechodniość złączenia

T10. _R( rs)  r oraz _S( rs)  s

T11. q _R(q _S(q

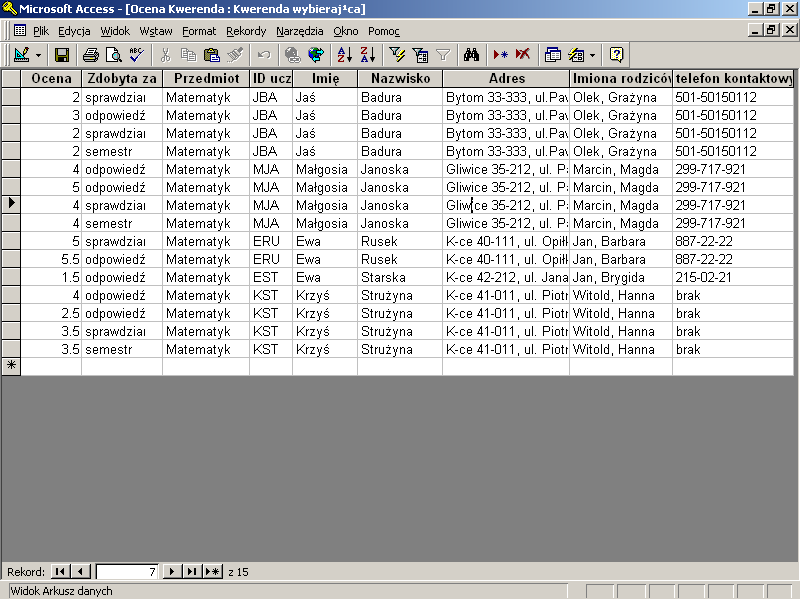
W wyniku złączenie tabel Uczeń i Ocena otrzymujemy tabelę zawierającą wyłącznie sensowne zestawienia krotek i dostarczającą nam pełnej informacji o ocenach uczniów.

Rys. 19.1 Wynik złączenia naturalnego tabeli Ocena z tabelą Uczeń

W rozdziale zamieściliśmy podstawowe informacje niezbędne osobie, która chce zaprojektować bazę danych. Jeżeli Czytelnik opanował ten materiał przy pierwszej lekturze tekstu, to prawdopodobnie w ogóle nie musiał go czytać. Osoba zupełnie nie znająca teorii relacyjnych baz danych prawdopodobnie będzie musiała wrócić do rozdziału 20 jeszcze kilkukrotnie.

W rozdziale nie została przedstawiona teoria normalizacji, dziedzina matematyki opisująca metody przekształcania modeli danych poprzez kolejne postacie normalne. Zainteresowanych pogłębieniem swoich wiadomości w tym zakresie odsyłamy do pozycji wymienionych w "Wykazie dostępnej literatury" na końcu książki.

Tytuł książki zobowiązuje autorów do ograniczenia "aparatu matematycznego" do poziomu szkoły średniej.

Liczba w nawiasie określa wielkość pola tekstowego, tzn. wartości atrybutu Id ucznia nie mogą przekroczyć 5 znaków.

Liczby w nawiasie określają skale i precyzję liczby, tzn. wartości atrybutu Ocena są liczbami z zakresu 0,0-9,9

Nie wymieniliśmy tu wszystkich spełnionych przez omawianą relację zależności funkcyjnych. W praktyce projektant wybiera zależności funkcyjne pod kątem konkretnego zastosowania bazy danych.

Iloczyn kartezjański tabeli Uczeń i Ocena tworzy 5*15=75 kombinacji wartości, z których ogromna większość nie niesie ze sobą żadnej informacji.

Jeżeli w danym modelu t. 10 przybiera formę równości, znaczy to, że podczas łączenia nie tracimy informacji przechowywanych w łączonych relacjach

Jeżeli w danym modelu t. 11 przybiera formę równości, znaczy to, że relacja rozkłada się z zachowaniem informacji.

6 Część I ♦ Podstawy obsługi systemu WhizBang (Nagłówek strony)

6 C:\My Documents\MATURA\R-19.DOC

---