WYTRZYMAŁOŚĆ MATERIAŁÓW

LABORATORIUM

1. Obciążenie - są to siły przyłożone do konstrukcji. Obciążenie w postaci sił dzielimy na:

1. Siły skupione - są to obciążenia przenoszące się na daną konstrukcję przez bardzo małe, w stosunku do wielkości konstrukcji lub jej części poletka, np. nacisk kół samochodu na nawierzchnię drogi.

2. Siły rozłożone - są to obciążenia przyłożone w sposób ciągły na pewnym odcinku długości lub wycinku pola powierzchni konstrukcji, np. półka z książkami. Siły rozłożone można podzielić na:

1. Siły rozłożone równomiernie,

2. Siły rozłożone nierównomiernie.

2. Obciążenie statyczne, działający na konstrukcję w sposób nie zmieniający wielkości ani kierunku sił.

3. Obciążenia dynamiczne, stanowią siły przyłożone do konstrukcji w sposób nagły powodujący wzrost wartości sił przyłożonych do konstrukcji do określonej wartości w bardzo krótkim czasie.

4. Odkształcenie - jest to miara deformacji ciała poddanego siło zewnętrznym. Dana konstrukcja pod wpływem działających na nie obciążeń zmienia swoje wymiary i kształty. Rodzaj i wielkość odkształceń materiałów zależy od budowy wewnętrznej materiałów, czyli ich struktury. Odkształcenia dzielimy na:

1. Odkształcenia sprężyste, występują wówczas, gdy zmiany wymiarów obciążonego elementu znikają po zdjęciu obciążenia.

2. Odkształcenia trwałe, występują wtedy, gdy po usunięciu obciążenia dany element nie powróci już do pierwotnych wymiarów.

5. Odkształcenie niszczące - jest to wielkość odkształceń po osiągnięciu której materiał traci swoją ciągłość, czyli jego struktura ulega zniszczeniu.

6. Formy przedstawiania wielkości odkształceń.

1. Odkształcenie bezwzględne, jest wyrażana jako dodatni lub ujemny przyrost wymiarów mierzonych w jednostkach długości Δl = l-l_o , gdzie Δl: odkształcenie bezwzględne, l: długość materiału po odkształceniu, l_o: początkowa długość materiału

2. Odkształcenie względne, czyli odkształcenie właściwe, wyrażane rachunkowo jako wartość bezwymiarowa podawana w formie ułamka lub promili, ε = Δl/l_o =l-10/l_o

7. Naprężenie - jest to wielkość sił przypadająca na jednostkę pola powierzchni przekroju danego materiału. Naprężenie jest reakcją wewnętrzną na obciążenie zewnętrzne, zależy więc od rodzaju i sposobu przyłożenia obciążenia zewnętrznego.

Naprężenia ze względu na siły zewnętrzne dzielimy na:

1. Naprężenia normalne - mają kierunek działania prostopadły do przekroju

σ = P / F [N/m²] , gdzie P: wartość sumy sił wewnętrznych [N], F: pole przekroju powierzchni [m²]

2. Naprężenia styczne - mają kierunek działania równoległy do przekroju

τ = T / F [N/m²] , gdzie T: wartość sumy sił wewnętrznych [N], F: pole przekroju powierzchni [m²]

8. Naprężenia dopuszczalne - są to naprężenia, które mogą występować w materiale bez obawy naruszenia warunku wytrzymałości i warunku sztywności. Oznaczamy je litera „k” z odpowiednim indeksem dolnym, charakteryzującym rodzaj odkształcenia. Naprężenia dopuszczalne „k: można ogólnie określić wzorem: k = R / n , gdzie: R: granica wytrzymałości, n: współczynnik bezpieczeństwa.

9. Wytrzymałość materiału na ściskanie (R_c)

Parametr (R_c) jest cechą materiału charakteryzującą zdolność do przenoszenia naprężeń ściskających, określana wzorem: (R_c) = F_c / S_o [N/m²] , gdzie: F_c: siła niszcząca próbkę w trakcie ściskania [N], S_o; pole powierzchni [m²] prostopadłego do kierunku działania siły F_c

10. Wytrzymałość materiału na rozciąganie (R_m)

Parametr (R_m) podobnie jak (R_c) stanowi cechę materiału charakteryzującą jego zdolność do przenoszenia naprężeń rozciągających: (R_m) = F_m / S_o [N/m²] , gdzie: F_m: siła niszcząca próbkę w trakcie rozciągania, S_o: pole powierzchni przekroju [m²] prostopadłego do kierunku działania siły F

11. Ćwiczenie 1. Próba statyczna rozciągania metali. Teoria.

1. Rozciąganie - Składają się na nie dwie przeciwnie działające siły, powodujące wydłużenie ciała w kierunku linii działania tych sił.

Elementy pracujące na rozciąganie nazywamy prętami i cięgnami.

2. 
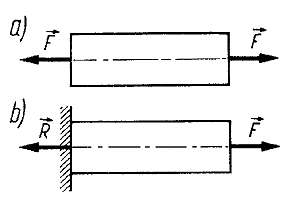
   Statyczna próba rozciągania. Badanie polega na osiowym rozciąganiu znormalizowanej próbki ze stałą szybkością w temperaturze pokojowej (10-35 °C), obniżonej lub podwyższonej, aż do jej zerwania. Próbką jest odpowiednio przygotowany pręt o znormalizowanych wymiarach. Próbę przeprowadza się wykorzystując urządzenie zwane zrywarką. W czasie próby rejestruje się zależność siły rozciągającej od przyrostu długości próbki.

3. Wykres rozciągania.

1. 
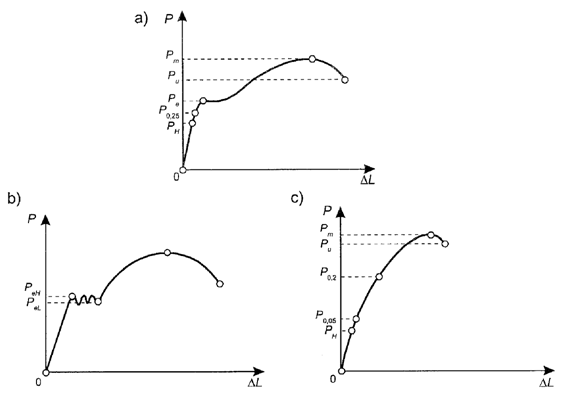
   Dla materiałów wykazujących wyraźną granicę plastyczności, gdzie P_H: granica proporcjonalności, P_0,25 : granica sprężystości, P_e: granica plastyczności, P_m: wytrzymałość na rozciąganie, P_w: naprężenie zrywające

2. Dla materiałów wykazujących górną i dolną granicę plastyczności, gdzie P_eH: górna granica plastyczności, P_el: dolna granica plastyczności

3. Dla materiałów bez wyraźnej granicy plastyczności

4. Granica proporcjonalności - maksymalne naprężenie, przy którym zachodzące odkształcenie jest proporcjonalne do wywołującego je naprężenia. Jest to granica liniowej sprężystości, a więc obowiązywania prawa Hooke'a.

5. Prawo Hooke'a - prawo mechaniki określające zależność odkształcenia od naprężenia. Głosi ono, że odkształcenie ciała pod wpływem działającej na nie siły jest wprost proporcjonalne do tej siły. Współczynnik między siłą a odkształceniem jest często nazywany współczynnikiem (modułem) sprężystości.

6. Granica sprężystości - to takie naprężenie, po przekroczeniu którego ciało nie powraca do pierwotnego kształtu po usunięciu naprężenia. W materiale pozostają trwałe deformacje.

7. Wyraźna granica plastyczności - występuje na wykresach rozciągania materiałów eloplastycznych, jak np. stal niskowęglowa. Jest to naprężenie rozciągające, po osiągnięciu którego obserwuje się wyraźny wzrost rozciąganej próbki bez wzrostu obciążenia.

8. Umowna granica plastyczności - określa się ją tylko dla materiałów nie mających wyraźnej granicy plastyczności. Określa się ją jako wartość naprężenia rozciągającego, które wywołuje w próbce wydłużenie trwałe = 0,2 % pierwotnej długości pomiarowej próbki.

9. Górna i dolna granica plastyczności - jeżeli w okolicach plastyczności następuje wyraźna oscylacja naprężenia, to wyróżnia się górna i dolna granicę plastyczności

10. Wytrzymałość na rozciąganie - jest to naprężenie rozciągające, przy którym siła obciążenia uzyskuje maksymalną wartość

11. Moduł Younga - inaczej moduł sprężystości podłużnej (E) - wielkość określająca sprężystość materiału. Wyraża ona, charakterystyczną dla danego materiału, zależność względnego odkształcenia liniowego ε materiału od naprężenia σ, jakie w nim występuje w zakresie odkształceń sprężystych.. Moduł Younga dany jest wzorem: E = σ / ε [Pa]

12. Współczynnik Poissona (ν) jest stosunkiem odkształcenia poprzecznego do odkształcenia podłużnego przy osiowym stanie naprężenia. Współczynnik Poissona jest wielkością bezwymiarową i nie określa sprężystości materiału, a jedynie sposób, w jaki się on odkształca.

13. Wydłużenie względne - stosunek zmiany długości próbki w momencie zerwania do długości początkowej próbki, wyrażony w procentach, dane wzorem

A = [ (l_u - l_o) / l_o ] x 100% , gdzie l_o : początkowa długość pomiarowa, l_u: długość pomiarowa po zerwaniu

14. Przewężenie względne - stosunek zmniejszenia się pola przekroju poprzecznego w miejscu zerwania do pola przekroju poprzecznego roboczej części próbki nieobciążonej, wyrażony w procentach. Dane jest wzorem: Z = [ (S_o - S_u) / S_o ] x 100%, gdzie: S_u: pole najmniejszego przekroju poprzecznego próbki po zerwaniu, S_o: pole przekroju poprzecznego roboczej części nieobciążonej próbki.

12. Ćwiczenie 2. Próba statyczna ściskania materiałów kruchych.

1. Ściskanie - rodzaj obciążenia ciała (elementu konstrukcyjnego), na które składają się dwie przeciwnie działające siły F, powodujące ściśnięcie ciała w kierunku linii działania tych sił.

2. 
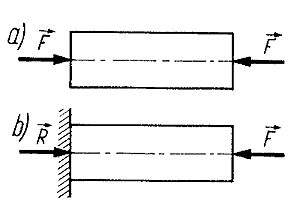
   Próbę statyczną ściskania stosuje się głównie przy badaniu materiałów kruchych, czyli nie wykazujących zdolności do znacznych odkształceń plastycznych, takich jak beton, cegła, skały. Materiały kruche mają znacznie większą wytrzymałość na ściskanie (R_c ) niż wytrzymałość na rozciąganie (R_m)

3. Moduł Younga ( podpunkt 11.11.)

4. Próba wytrzymałościowa na ściskanie jest podstawową próbą w badaniach wytrzymałościowych materiałów. Polega na określaniu granicznych wartości sił ściskających, powodujących zniszczenie elementu lub trwałe odkształcenie, które uniemożliwia dalsze jego użytkowanie.

5. Wyboczenie w wytrzymałości materiałów - zjawisko gwałtownego przejścia od jednej postaci deformacji - osiowego ściskania pręta do jakościowo innej postaci deformacji - zginania. Zjawisko to powoduje gwałtowną redystrybucję sił wewnętrznych, przez co jest niebezpieczne dla konstrukcji. Zjawisko wyboczenia jest szczególnym przypadkiem szerszej grupy zjawisk określanych jako utrata stateczności konstrukcji.

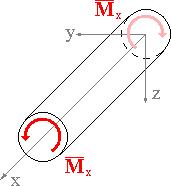
13. Ćwiczenie 3. Próba statyczna skręcania. Teoria.

1. 
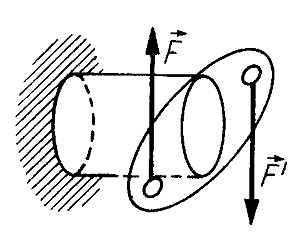
   Skręcanie - wywołane jest siłami dającymi moment skręcający, pod którego działaniem poszczególne przekroje poprzeczne przedmiotu zostają obrócone względem siebie wokół pewnej osi.

Typowym przykładem elementów skręcanych są wały maszyn.

2. Wyróżniamy dwa rodzaje skręcania

1. 
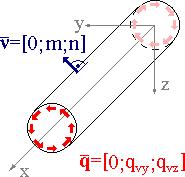
   Skręcanie czyste - w którym do ścianek poprzecznych jednorodnego i izotropowego pręta pryzmatycznego przyłożone jest obciążenie o gęstości q= [0;q_vy;q_vz], które redukuje się do dwóch przeciwnie skierowanych momentów działających w płaszczyźnie ścianek poprzecznych.

2. Skręcanie proste pręta, które różni się od skręcania "czystego" tym, że obciążenie zastępujemy dwójką przeciwnie skierowanych, równych co do wartości skupionych momentów skręcających.

3. Moduł Kirchhoffa (G) (inaczej moduł odkształcalności postaciowej albo moduł sprężystości poprzecznej) - współczynnik uzależniający odkształcenie postaciowe materiału od naprężenia, jakie w nim występuje. Jednostką modułu Kirchhoffa jest paskal. Jest to wielkość określająca sprężystość materiału. Moduł ten dany jest wzorem:

G = τ / γ , gdzie: τ: naprężenie ścinające, γ: odkształcenie postaciowej

4. 
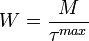
   Wskaźnik wytrzymałości na skręcanie - w mechanice wielkość charakteryzująca odporność prętów na skręcanie. Wskaźnik wyraża iloraz momentu skręcającego pręt i naprężenia stycznego w pręcie

5. Granica proporcjonalności postaciowej (podpunkt 11.4.)

6. Granica sprężystości (podpunkt 11.6.)

7. Granica plastyczności (podpunkt 11.7.)

8. Biegunowy moment bezwładności przekroju (tylko kołowego lub pierścieniowego) belki jest parametrem przekroju opisującym wytrzymałość na skręcanie. Gdy przemnożymy biegunowy moment przekroju razy moduł Kirchhoffa, to otrzymamy sztywność na skręcanie belki. Biegunowy moment bezwładności to moment bezwładności względem punktu będącego środkiem ciężkości.

9. Moment skręcający - w mechanice moment pary sił, którego wektor jest równoległy do osi elementu skręcanego, najczęściej pręta lub wału.

O wielkości skręcenia na jednostkę długości pręta, wywołanego przez dany moment skręcający decydują:

wytrzymałość materiału, z którego wykonany jest poddany skręcaniu element, charakteryzowana przez moduł Kirchhoffa,

„sztywność" przekroju konkretnego pręta, wyrażana przez wskaźnik wytrzymałości na skręcanie.

14. Ćwiczenie 4. Próba statyczna ścinania technologicznego. Teoria.

1. Ścinanie. Wywołane jest działaniem dwóch sił tworzących parę sił, powodują w ostateczności ścięcie elementu.

Na ścinanie pracują przede wszystkim nity, śruby, sworznie i spoiny.

2. 
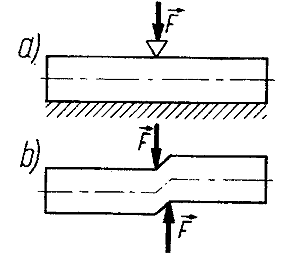
   Stan naprężenia w przekrojach, w których występują tylko naprężenia styczne, nazywamy czystym ścinaniem.

Prawo Hooke'a dla czystego ścinania:

Naprężenie styczne t jest proporcjonalne do odkształcenia postaciowego g.

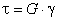
gdzie G - moduł sprężystości postaciowej. W elementach konstrukcyjnych spotykanych w technice można znaleźć takie przekroje, w których występuje czyste ścinanie, np. podczas czystego skręcania. W przeważającej liczbie przypadków w przekrojach elementów konstrukcyjnych występują jednocześnie naprężenia normalne i styczne.

Ścinaniem technologicznym nazywamy naprężenia i odkształcenia materiału spowodowane dwiema siłami tworzącymi parę o bardzo małym ramieniu.

15. Ćwiczenie 5. Próba statyczna ściskania sprężyn śrubowych. Teoria.

1. Ściskanie (podpunkt 12.1.)

2. Sprężyna śrubowa - rodzaj sprężyny wykonanej z drutu okrągłego, kwadratowego lub prostokątnego ukształtowanego w formie linii śrubowej. W zależności od kierunku nawinięcia sprężyny dzieli się na prawo- lub lewoskrętne, przy czym skok zwojów sprężyny może być stały lub zmienny.

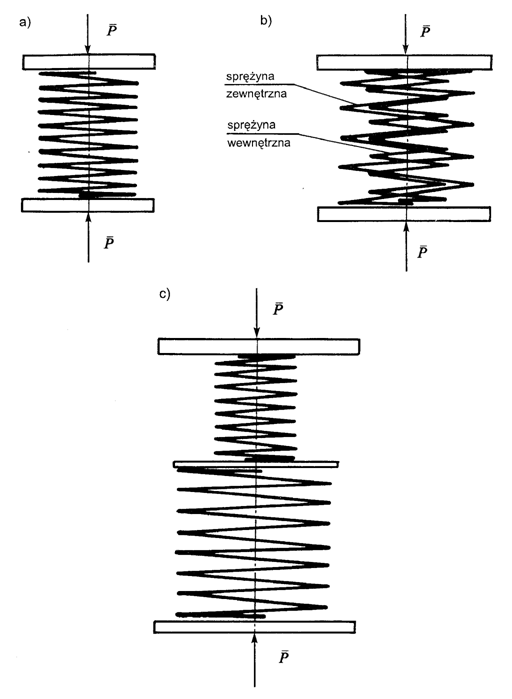
3. Ściskanie sprężyn w układzie:

1. pojedynczym

2. równoległym

3. szeregowym

4. Moduł sprężystości postaciowej (podpunkt 13.3.)

5. Stała sprężyny (c) to siła, z którą działa sprężyna przy 1 mm ściskania (rozciągania w przypadku sprężyny naciągowej), jest ona wielkością proporcjonalną w przypadku sprężyn cylindrycznych. (patrz wykres)

c = Fn / fn

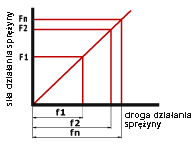
Maksymalną siłą, z jaką działa sprężyna jest zatem Fn, o ile sprężyna ma określone naprężenia wstępne, zwane są one zwykle F1. Wartość Fn jest decydująca dla wykonania sprężyny.

6. Stan naprężeń w sprężynie ściskanej pionową siła (P)

W przekroju sprężyny działają następujące obciążenia: siła P oraz moment wywołany przez tę siłę - M = PR. Ich składowe pokazano na rysunku poniżej:

W przekroju sprężyny działają następujące obciążenia: siła P oraz moment wywołany przez tę siłę - M = PR. Moment M ma składowe: Mx = PR sin α = Mg (wywołujący zginanie) i My = PR cos α = Ms (wywołujący skręcanie), natomiast siła P: Px= P sin α = N (wywołująca ściskanie) oraz Py = P cos α = T (wywołująca ścinanie). Jeśli pochylenie zwojów jest małe (α bliskie zeru), to w przekroju dominują naprężenia styczne od skręcania i ścinania.

16. Ćwiczenie 6. Próba statyczna zginania. Teoria.

1. Zginanie. Wywołane jest działaniem sił prostopadłych do osi belki i leżącymi w płaszczyźnie zawierającej tę oś lub równoległej do niej.

Typowe elementy zginane to: belki, osie i wały maszyn. W praktyce częściej spotykanymi odkształceniami są odkształcenia złożone (jednoczesne zginanie i skręcanie, zginanie ukośne, zginanie z rozciąganiem lub ściskaniem).

2. 
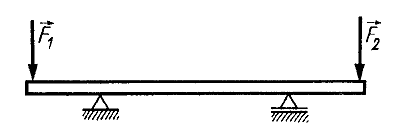
   Schemat zginania siła (P) obciążoną w środku, oraz dwiema siła (P/2)

3. 
   
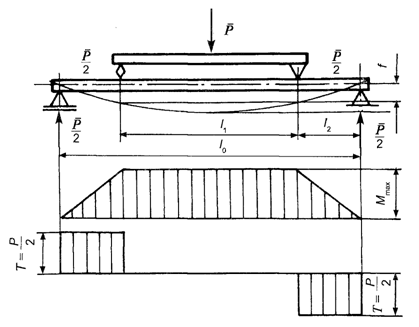
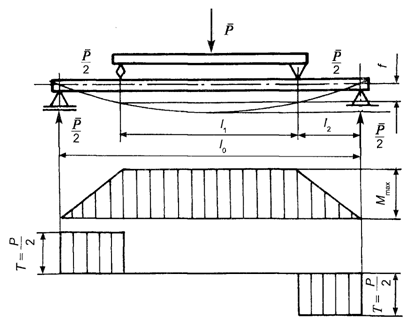
   Moduł sprężystości podłużnej (E) (podpunkt 11.11.)

4. Ze względów technicznych, dla materiałów liniowo-sprężystych, rozróżnia się kilka przypadków szczególnych zginania:

1. czyste zginanie - naprężenia w przekroju redukują się jedynie do momentu zginającego, brak jest sił podłużnych i sił poprzecznych (ścinających),

2. proste zginanie - naprężenia redukują się do momentu i sił poprzecznych,

3. ściskanie/rozciąganie mimośrodowe - naprężenia redukują się do momentu i siły podłużnej, siły poprzeczne mogą ale nie muszą wystąpić.

Zginanie jest pokrewne rozciąganiu i ściskaniu, gdyż powoduje pojawienie się naprężeń normalnych w przekrojach poprzecznych elementu. W przeciwieństwie jednak do rozciągana i ściskania, rozkład naprężeń normalnych w przekroju elementu jest nierównomierny.

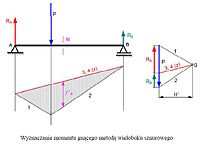
5. Moment gnący w dowolnym przekroju belki zginanej to algebraiczna suma momentów sił zewnętrznych działających po jednej stronie (lewej lub prawej) rozważanego przekroju względem środka masy tego przekroju.

6. 
   

---