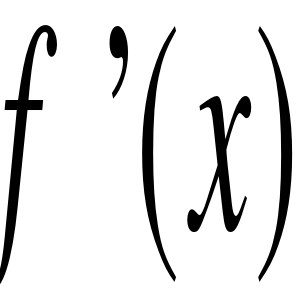Przykładowe zadania na zaliczenie matematyki z semestru 1 z rozwiązaniami

1. Oblicz granice funkcji
w punkcie

Rozwiązanie: Punkt
nie należy do dziedziny funkcji (mianownik jest zerowy), tym samym wyznaczamy granice jednostronne.

Zapis
czytamy „prawie 6 w liczniku i prawie zero w mianowniku, ale ze znakiem minus”. Wartością ułamka, gdzie w liczniku jest liczba różna od zera, a mianownik bliski zera jest zawsze nieskończoność z odpowiednim znakiem.

2. Wyznacz dziedzinę funkcji
i jej granice na krańcach dziedziny

Rozwiązanie: dziedziną tej funkcji jest zbiór liczb rzeczywistych z wyłączeniem liczby -3 (bo mianownik nie może być równy zero). Można to zapisać tak:

Wyznaczamy teraz granice na krańcach dziedziny, przy czym granice w plus (minus) nieskończoności wyznaczymy zgodnie z komentarzem do zadania 2.

Granice jednostronne w punkcie -3 wyznaczamy zgodnie z rozwiązaniem zadania 3.

3. Czy funkcja
ma asymptotę poziomą? Jeżeli tak, to proszę podać jej równanie.

Rozwiązanie: łatwo zauważyć, że granice tej funkcji w minus i plus nieskończoności są równe 3, tym samym prosta y=3 jest asymptotą poziomą tej funkcji.

Inna metoda, to pełne badanie czy istnieje asymptota ukośna
(pozioma to szczególny przypadek ukośnej, gdy parametr
):

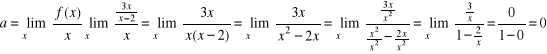
Ostatecznie prosta
jest asymptotą (poziomą) funkcji

4. Czy funkcja
posiada asymptotę ukośną? Jeżeli tak, to podaj jej równanie.

Rozwiązanie: znajdujemy granice na parametr a i b zgodnie z komentarzem do zadania 5. Jeżeli będą to granice skończone, to istnieje asymptota ukośna o równaniu

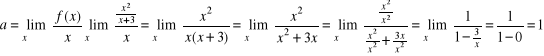
Obie granice są skończone, w takim razie prosta
jest asymptotą poziomą tej funkcji.

5. Oblicz pochodną funkcji

Rozwiązanie: funkcja
jest złożeniem dwóch funkcji:

Zgodnie z zasadą wyznaczania pochodnej funkcji złożonej (pochodna funkcji zewnętrznej razy pochodna funkcji wewnętrznej) mamy:

6. Oblicz pochodną funkcji

Rozwiązanie: funkcja
jest „potrójnie” złożona

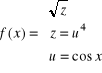
Zgodnie z zasadą wyznaczania pochodnej funkcji złożonej (pochodna funkcji zewnętrznej razy pochodna funkcji wewnętrznej) mamy:

7. Oblicz pochodną funkcji

Rozwiązanie: korzystamy z wzoru na pochodną ilorazu dwóch funkcji:

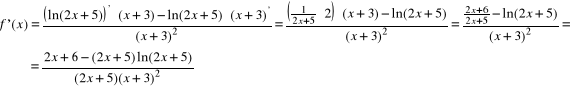
Przy wyznaczaniu pochodnej funkcji licznika musieliśmy skorzystać z wzoru na pochodną funkcji złożonej.

8. Proszę naszkicować wykres funkcji
, o której mamy następujące informacje:

D:

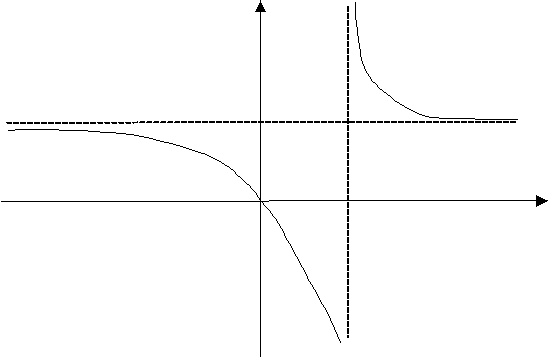
Z treści pytanie wiemy, że prosta
jest asymptotą pionową, a z granic jednostronnych w tym punkcie znamy zachowanie funkcji po obu stronach asymptoty. Wiemy także, że w punkcie
wykres funkcji przecina oś x-ów (miejsce zerowe).

Z zapisu
wynika, że prosta
jest asymptotą poziomą (zobacz zadanie 5). To są wystarczające informacje dla naszkicowania wykresu tej funkcji.

9. Wyznacz przedziały monotoniczności funkcji

Rozwiązanie: zaczynamy od wyznaczenia pochodnej naszej funkcji:

Badamy, kiedy pochodna jest większa od zera, a kiedy mniejsza od zera.

Przy rozwiązywaniu tych dwóch nierówności korzystamy z wykresu funkcji kwadratowej o miejscach zerowych -6 i 0 oraz gałęziach paraboli skierowanych do góry.

Ostatecznie funkcja
jest rosnąca dla
, a malejącą dla
. Z uwagi na dziedzinę funkcji musieliśmy przedział
przekształcić na sumę dwóch przedziałów.

10. W wyniku prowadzonego badania przebiegu zmienności funkcji uzyskano następującą tabelkę:

x		...	-1	...	0	...	1	...
		-		-	0	-		-
		-		+	0	-		+
	0		Nie istnieje		0		Nie istnieje		0

Proszę naszkicować wykres tej funkcji.

Analizując informacje zawarte w podanej tabeli widzimy, że badana funkcja ma asymptoty pionowe w punktach
oraz
. Widzimy także, że w punkcie
wartość funkcji jest zerowa.

Widzimy także, że granice tej funkcji w minus (plus) nieskończoności są skończone i równe 0, co jak wiemy oznacza, że funkcja posiada asymptotę poziomą o równaniu
(zobacz zadanie 5).

Z analizy pierwszej pochodnej wynika, że w całej dziedzinie badana funkcja maleje (pierwsza pochodna ujemna), z uwagi na różny znak drugiej pochodnej funkcja będzie miała albo kształt wypukły, albo wklęsły. Słownie jej przebieg można opisać następującą (wartości x-ów rosną od minus do plus nieskończoności):

Wartości funkcji maleją od prawie zera do minus nieskończoności po lewej stronie asymptoty
, przy czym wykres funkcji jest wypukły (druga pochodna ujemna). Po drugiej stronie asymptoty funkcja maleje od plus nieskończoności do zera, którą przyjmuje w
, po przekroczeniu zera dalej maleje aż do minus nieskończoności po lewej stronie asymptoty
. W przedziale
funkcja najpierw ma kształt wklęsły, a później wypukły (druga pochodna jest dodatnia dla
- kształt wklęsły i ujemna dla
- kształt wypukły. Po drugiej stronie asymptoty
funkcja maleje od plus nieskończoności do zera kształtem wklęsłym.

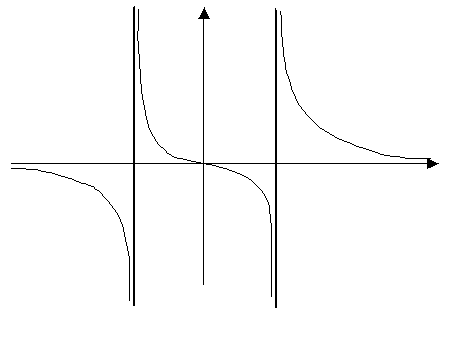
Niezdarny szkic wykresu pokazany jest niżej.

---