I tura

1. Co to jest dystrybuanta zmiennej losowej? Podaj wzory dla zmiennej skokowej i ciągłej.

Dystrybuantą zmiennej losowej X nazywamy funkcję zdefiniowaną następująco: F(x) = P(X<x).

Dystrybuanta zm. skokowej: F(x) =

Dystrybuanta zm. ciągłej: F(x) =
dla

2. Opisz rozkład Poissona i jego zastosowania.

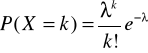
Rozkład Poissona jest to rozkład zmiennej losowej skokowej, przedstawiający liczbę wystąpień badanego zjawiska w czasie t, w określonej liczbie prób, jeśli wystąpienia tego zjawiska są niezależne od siebie.

Funkcja prawdopodobieństwa w rozkładzie Poissona ma postać:

Rozkład ten ma zastosowanie do obliczenia przybliżonej wartości prawdopodobieństwa w rozkładzie dwumianowym przy dużej liczbie prób i niskim prawdopodobieństwie sukcesu.

3. Wyjaśnij pojęcia: współczynnik (poziom) ufności i poziom istotności.

Współczynnik ufności (1-α) - jest to prawdopodobieństwo tego, że wyznaczając (na podstawie n-elementowych prób) dolną i górną granicę przedziału, nieznana wartość parametru znajdzie się w tym przedziale.

Poziom istotności (α) - prawdopodobieństwo wystąpienia błędu I-go rodzaju.

4. Zapisz wzory na estymację punktową dla wartości oczekiwanej, wariancji, wskaźnika struktury.

Dla wartości oczekiwanej:

Dla wariancji:

5. Zapisz hipotezy, statystykę oraz obszar krytyczny przy weryfikacji hipotezy z wariancji, która jest mniejsza niż 25, dla próby o liczebności 130.

;

Statystyka:
(bo mała próba) + wzór obok jako chi-kwadrat.

Obszar krytyczny lewostronny (po minusowej części układu współrzędnych zaznaczamy
i zakreskowujemy wszystko w lewo (do -∞).

6. Zapisz hipotezy oraz statystykę przy badaniu istotności współczynnika korelacji.

(współczynnik NIE jest istotny statystycznie - zmienne NIE są skorelowane)

(współczynnik jest istotny statystycznie - zmienne są skorelowane)

Statystyki:

+ dla małej próby (n ≤ 120):

+ dla dużej próby (n > 120): z

II tura

1. Co to jest rozkład prawdopodobieństwa zmiennej losowej? Co to są rozkłady zmiennej skokowej i ciągłej?

Rozkład prawdopodobieństwa zmiennej losowej jest to funkcja przyporządkowująca wartościom
prawdopodobieństwa
.

Dla zmiennej losowej skokowej jest to funkcja prawdopodobieństwa:

Dla zmiennej losowej ciągłej jest to funkcja gęstości, (nieujemnie):

2. Rozkład normalny i jego zastosowania.

Rozkład normalny jest jednym z najważniejszych rozkładów zmiennej losowej ciągłej. Zmienna losowa X ma rozkład normalny, jeżeli jej funkcja gęstości prawdopodobieństwa wyraża się wzorem:

Charakteryzują go dwa parametry: wartość oczekiwana i odchylenie standardowe. Rozkład normalny jest rozkładem symetrycznym, ponieważ: Średnia = Mediana = Dominanta.

Zastosowania:

• waga i wzrost osobników jednorodnych populacji ludzkich i zwierzęcych;

• losowe błędy pomiarów;

• iloraz inteligencji.

3. Wyjaśnij pojęcia: parametr, estymator, ocena parametru.

Parametr (θ) - charakterystyka określająca całą populację.

Estymator (
) - pewna funkcja określona na próbie, która służy do oszacowania nieznanej wartości parametru θ.

Ocena parametru (T) - jest to konkretna wartość liczbowa, którą przyjmuje estymator dla realizacji próby.

4. Zapisz wzory na estymację punktową dla wartości oczekiwanej, odchylenia standardowego i wskaźnika struktury.

Dla wartości oczekiwanej:

Dla odchylenia standardowego:
[???]

5. Zapisz hipotezy, statystykę oraz obszar krytyczny przy weryfikacji hipotezy, że średnia jest mniejsza od 25, dla próby o liczebności 150.

;

Statystyka:
(bo duża próba)

Obszar krytyczny lewostronny (po minusowej części układu współrzędnych zaznaczamy
i zakreskowujemy wszystko w lewo (do -∞).

6. Zapisz hipotezy oraz statystykę przy badaniu istotności współczynnika regresji.

(współczynnik NIE jest istotny statystycznie - pomiędzy zmiennymi NIE występuje zależność)

(współczynnik jest istotny statystycznie - pomiędzy zmiennymi występuje zależność)

Statystyka:

---