BLOK III

model wielokrotnej regresji liniowej - odmiana jakościowa - kodowanie

quasi-eksperymentalne

Tabela 1

Kodowanie quasi-eksperymentalne zmiennej jakościowej A (miejsce zamieszkania o p=4 kategoriach, n=3

(0)	(1)	(2)	(3)	(4)	(5)
	Kategorie	Zmienna	Zmienne instrumentalne
Lp	zmiennej A	zależna Y	T1	T2	T3
1	wieś	Y11	1	0	0
2	a1	Y12	1	0	0
3		Y13	1	0	0
4	małe	Y21	0	1	0
5	miasto	Y22	0	1	0
6	a2	Y23	0	1	0
7	średnie	Y31	0	0	1
8	miasto	Y32	0	0	1
9	a3	Y33	0	0	1
10	duże	Y41	-1	-1	-1
11	miasto	Y42	-1	-1	-1
12	a4	Y43	-1	-1	-1
Suma		Y..	0,0	0,0	0,0

Przykład

(0)	(1)	(2)	(3)	(4)
	Zmienna A
Lp.	a1	a2	a3	a4
1	2	8	18	25
2	3	10	19	28
3	2	12	19	30
Suma	7	30	56	83
Średnia	2,33333	10,00000	18,66666	27,66666

p=4 n=3 N=pn=12 Y..=176,0, średnia =14,66667

Tabela ANOVA-A

(0)	(1)	(2)	(3)	(4)
Źródło war. Y	SS	df	MS	F
Między	1076,6667	3	358,889	130,505**
Wewnątrz	22	8	2,75
Cała	1098,6667	11

* p<0,05 F_{0,05; 3; 8} = 4,07

** p<0,01 F_{0,01; 3; 8} = 7,59

Tabela

Zakodowane dane z przykładu

(kodowanie quasi-eksperymentalne)

(0)	(1)	(2)	(3)	(4)	(5)
			Zmienne instrumentalne
Lp	Grupy	Y	1	2	3
1		2	1	0	0
2	a1	3	1	0	0
3		2	1	0	0
4		8	0	1	0
5	a2	10	0	1	0
6		12	0	1	0
7		18	0	0	1
8	a3	19	0	0	1
9		19	0	0	1
10		25	-1	-1	-1
11	a4	28	-1	-1	-1
12		30	-1	-1	-1
Suma		176	0,0	0,0	0,0
Średnia		14,66667	0,0	0,0	0,0
s		9,99394	0,73855	0,73855	0,73855
rYw			-0,93606	-0,65278	-0,33255
			0,87621	0,42612	0,11059

N=12, p=4, n=3

Wartość współczynnika korelacji wielokrotnej R_Y.123 oraz wartość współczynnika determinacji wielokrotnej
równa jest:

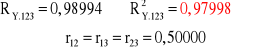
Współczynnik korelacji wielokrotnej może być obliczony z wzoru:

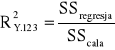
Tabela

Analiza wariancji dla regresji Y względem A - do danych z przykładu

(0)	(1)	(2)	(3)	(4)
Źródło wariancji Y	SS	df	MS	F
Regresja (R^2)	1076,66663	3	358,88889	130,505**
Odchylenie od regresji (reszta)	22,00000	8	2,75
Cała	1098,66663	11

* p<0,05 F_{0,05; 3; 8} = 4,07

** p<0,01 F_{0,01; 3; 8} = 7,59

Po podstawieniu danych z tabeli mamy:

Otrzymaliśmy następujące wartości współczynników regresji:

a=14,66667

b_Y1=-12,33333 b_Y2=-4,66667 b_Y3=4,00000

Łatwo sprawdzić, iż te same wartości współczynników regresji można otrzymać przyjmując za punkt wyjścia właściwości kodowania quasi-eksperymentalnego. I tak:

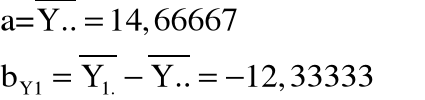
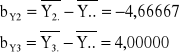
Równanie regresji przedstawia się zatem następująco:

Poszczególne efekty eksperymentalne możemy oszacować na podstawie:

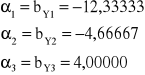
W jaki sposób korzystać z zapisanego wyżej równania regresji? Najlepiej pokazać to na przykładzie. Weźmy pod uwagę wynik osoby nr 1, tj. Y₁₁ (osoba z grupy a₁). W poszczególnych wektorach instrumentalnych T₁, T₂, T₃ uzyskała ona wyniki 1, 0, 0. Po podstawieniu tych wyników do równania regresji mamy:

SENS NADAWANY WSPÓŁCZYNNIKOM A I B

a - średnia całkowita zmiennej zależnej Y:

współczynniki b równają się odchyleniu danej średniej grupowej, dla której zmienna instrumentalna przyjmuje wartości +1, od średniej ogólnej.

dla grupy a:

dla grupy a₂

dla grupy a₃

Współczynniki b to tyle, co efekt eksperymentalny danego poziomu czynnika A (
), b_Y2 to tyle, co efekt eksperymentalny drugiego poziomu czynnika A (
) itd.

Określanie efektu eksperymentalnego czwartego poziomu czynnika A(), gdy w równaniu regresji występują jedynie, np., p-1 = 4-1 = 3 zmienne instrumentalne.

Efekt czwartego poziomu (odpowiadający grupie porównawczej, dla osób której wszystkie zmienne instrumentalne przyjmują wartości: -1) czynnika A (ogólnie p-tego poziomu) wyznaczamy korzystając z prawidłowości

Zatem:

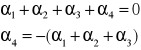
Ogólnie efekt eksperymentalny poziomu p czynnika A:

Wynik każdej osoby badanej Y_ik można rozbić na trzy składowe:

(a) średnią ogólną:

(b) efekt i-tego poziomu czynnika A rozumianego jako odchylenie i-tej średniej grupowej od średniej ogólnej
odpowiadają wartości współcz. regresji: b; efektowi poziomu p czynnika A odpowiada

(c) resztę, czyli

Całkowitą sumę kwadratów (SS_cała) możemy rozbić na sumę kwadratów dla regresji (SS_regresja) oraz na resztową sumę kwadratów (SS_reszta))

Zatem:

Równanie regresji ma postać:

Y' = b_Y1T₁ + b_Y2T₂ + b_Y3T₃ +a

Jerzy Brzeziński (2009) UAM - metodologia - zaawansowany.; BLOK III

1

---