WSTĘP TEORETYCZNY
Przyspieszenie ziemskie g jest to przyspieszenie, jakie nadaje siła ciężkości swobodnie spadającemu ciału, czyli siła, z jaką Ziemia przyciąga to ciało. Wartość g nie jest stała. Maleje w miarę jak rośnie wysokość. Wartość przyspieszenia zależy też od położenia punktu na powierzchni Ziemi. Zasadniczy wpływ ma fakt, iż kula ziemska ma kształt zbliżony do elipsoidy obrotowej, jest spłaszczona od strony biegunów. Odległość od jądra do powierzchni Ziemi jest najkrótsza właśnie na biegunach, zatem tam przyciąganie jest największe, najmniejszą wartość osiąga na równiku. Istotną rolę odgrywa także siła odśrodkowa, powstająca w czasie ruchu obrotowego Ziemi, która zmniejsza ciężar każdego ciała. Zmniejszenie to jest największe na równiku, a w miarę zbliżania się do bieguna maleje do zera. Wartość g zmienia się od około 9,78 m/s2 na równiku do około 9,83 m/s2 na biegunie. Niejednorodność budowy Ziemi, oraz ukształtowanie powierzchni Ziemi powodują niewielkie lokalne wahania wartości przyspieszenia.
Wahadło matematyczne jest jednym ze sposobów wyznaczania przyspieszeni ziemskiego, jest to punkt materialny, zawieszony na długiej, nieważkiej i nierozciągliwej nici znajdujący się w polu ciężkości.. Wahadło, wychylone o mały kąt z położenia równowagi, wykonuje ruch drgający prosty. Jest to ruch ciała zachodzący wokół stałego położenia równowagi. W przypadku ruchu okresowego położenie lub stan ciała powtarza się w jednakowych odstępach czasu ( = okres drgań T). Przyspieszenie ruchu wahadła w przypadku małych jego wychyleń (do 5o) jest proporcjonalne do wychylenia punktu materialnego z położenia równowagi i skierowane ku temu położeniu. W takiej sytuacji okres wahań wynosi:
gdzie:
![]()
l - długość wahadła
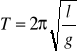
g - przyspieszenie ziemskie
Stąd wynika, że:
Wychylenie wahadła liczone po łuku koła o promieniu l wynosi:
s = lϕ
Momentem bezwładności nazywamy wielkość charakteryzująca sposób rozmieszczenia masy bryły wokół osi obrotu, w ruchu obrotowym bryły sztywnej, wielkość ta identyfikuje masę w ruchu po okręgu.
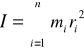
Momentem bezwładności I bryły względem danej osi nazywamy sumę iloczynów mas poszczególnych punktów bryły i kwadratów ich odległości od danej osi, a więc:
Tak zapisujemy moment bezwładności dla bryły sztywnej będącej zbiorem punktów materialnych.
W przypadku bryły o ciągłym rozkładzie masy, dzielimy ją w myśli na nieskończenie małe części i sumowanie w powyższym wzorze zastępujemy całkowaniem. W wyniku tych przekształceń otrzymujemy:
I = ∫ r²dm
gdzie:
dm - masa elementu objętości bryły odległego o r od osi.
Twierdzenie Steinera pozwala obliczyć moment bezwładności względem dowolnej osi, nie przechodzącej przez środek masy bryły, zgodnie z którym: moment bezwładności I bryły względem dowolnej osi jest równy sumie bezwładności I względem osi równoległej przechodzącej przez środek masy bryły oraz iloczynu masy tej bryły i kwadratu odległości a obu osi, czyli:
I = I0+ma²
W przypadku gdy oś przechodzi przez środek masy bryły do wyznaczenia momentu bezwładności posłuży nam metoda zawieszenia trójnitkowego.
Zasady dynamiki Newtona:
I zasada : Jeżeli na ciało nie działa żadna siła lub siły działające się równoważą to ciało pozostaje w spoczynku
lub porusza się ruchem jednostajnym prostoliniowym;
II zasada : Jeżeli na ciało działają siły, które nie równoważą się to ciało porusza się z przyśpieszeniem wprost
proporcjonalnym do siły wypadkowej: a = F/ m
III zasada : Jeżeli ciało A działa na ciało B z siłą FAB to ciało B działa na ciało A taką samą co do wartości siła
FBA , lecz skierowaną przeciwnie.
2. PRZEBIEG ĆWICZENIA :
2.1 WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA MATEMATYCZNEGO:
Żeby wyznaczyć wartość przyspieszenia ziemskiego skorzystamy wahadła matematycznego.
W tym celu mierzymy długość wahadła i okres wahań T.W pracowni zainstalowane są trzy wahadła o różnej długości. Wartość przyspieszenia ziemskiego obliczymy ze wzoru
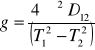
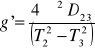
Kolejność wykonywanych czynności:
mierzymy długości wszystkich wahadeł,
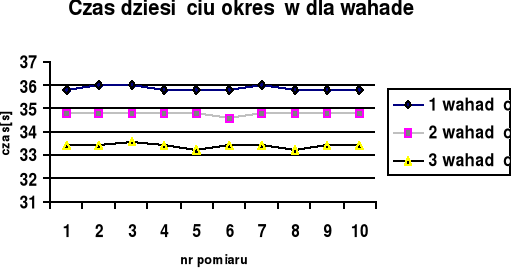
następnie dla każdego wahadła mierzymy czas dziesięciu okresów,
czynność tę powtarzamy 10 razy,
wyznaczamy przyspieszenie ziemskie dla wszystkich wahadeł-otrzymamy dwa wyniki
2.1.1. Tabele wyników:
a) Wahadło pierwsze -długość 144,5cm
Numer pomiaru |
Czas 10 drgań [s] |
1 |
35,8 |
2 |
36,0 |
3 |
36,0 |
4 |
35,8 |
5 |
35,8 |
6 |
35,8 |
7 |
36,0 |
8 |
35,8 |
9 |
35,8 |
10 |
35,8 |
tśr |
35,86 |
b) Wahadło drugie-długość 135,5cm
Numer pomiaru |
Czas 10 drgań [s] |
1 |
34,8 |
2 |
34,8 |
3 |
34,8 |
4 |
34,8 |
5 |
34,8 |
6 |
34,6 |
7 |
34,8 |
8 |
34,8 |
9 |
34,8 |
10 |
34,8 |
tśr |
34,78 |
c) Wahadło trzecie-długość 126,5cm
Numer pomiaru |
Czas 10 drgań [s] |
1 |
33,4 |
2 |
33,4 |
3 |
33,6 |
4 |
33,4 |
5 |
33,2 |
6 |
33,4 |
7 |
33,4 |
8 |
33,2 |
9 |
33,4 |
10 |
33,4 |
tśr |
33,38 |
T1 = 2,39 s D12 = 144,5 - 135,5 = 9 cm = 0,09 m
T2 = 2,32 s D23 = 135,5 - 126,5 = 9 cm = 0,09 m
T3 = 2,23 s
2.1.2. Wyniki:
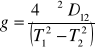
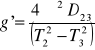
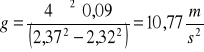
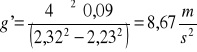
2.1.3. Analiza błędów:
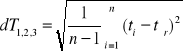
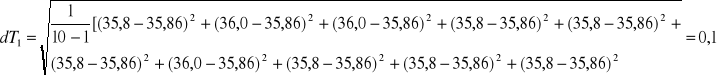
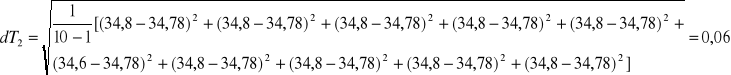
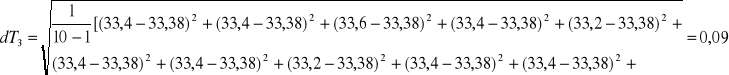
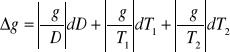
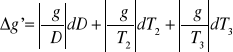
dD = 0,001 m
dT1 = 0,1
dT2 = 0,06
dT3 = 0,09
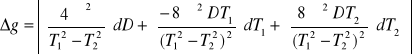
![]()
4,0
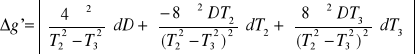
![]()
![]()
g = 10,77![]()
4,0 ![]()
g'= 8,67![]()
2,7 ![]()
2.2. WYZNACZANIE MOMENTÓW BEZWŁADNOŚCI BRYŁ SZTYWNYCH METODĄ ZAWIESZENIA TRÓJNITKOWEGO
Do wyznaczenia momentów bezwładności brył sztywnych skorzystamy z metody zawieszenia trójnitkowego. Wykorzystamy do tego celu przyrząd przedstawiony na rysunku
Przyrząd stanowi jednorodna tarcza o promieniu R0 zawieszona na trzech pionowych nitkach o długości l przymocowanych do tarczy w równych odległościach od środka O tarczy w wierzchołkach trójkąta równobocznego.
Kolejność wykonywanych czynności:
na tarczy kładziemy przedmiot którego moment bezwładności chcemy policzyć-oś główna bezwładności bryły powinna pokrywać się z osią tarczy OO',
obracamy tarczę o niewielki kąt-tutaj 20 stopni-puszczamy tarczę i włączamy stoper; tarcza zostaje wprawiona w drgania proste,
mierzymy czas dziesięciu okresów,
czynność powtarzamy 6 razy;
następnie ze wzoru
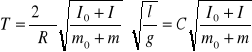
gdzie
l - długość nici
R0 = 12,7 cm = 0,127 m - promień tarczy kołowej
I0 - moment bezwładności tarczy
I - moment bezwładności bryły
m0 - masa tarczy
m -masa bryły
g = 9,81m/s² - przyspieszenie ziemskie
R = 12,2cm = 0,122 m - odległość środka tarczy od nici
T - okres drgań
wyznaczamy ![]()
i wyliczamy moment bezwładności każdej bryły,
Stałą przyrządu 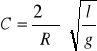
wyliczamy ze zmierzonych wartości R i l.
Dla pierwszej tarczy C1 = 15,34
Dla drugiej tarczy C2 = 15,16
Moment bezwładności tarczy wyliczamy z zależności ![]()
.
Dla pierwszej tarczy I1 = 0,00135 ![]()
Dla drugiej tarczy I2 = 0,00145 ![]()
2.2.1. Tabele wyników:
a) Drewniany prostopadłościan masa 140 g = 0,14 kg
wymiary 8,0 x 8,0 x 4,6 [cm]
Wahadło pierwsze Wahadło drugie
długość nici 87cm = 0,87 m długość nici 85 cm = 0,85 m
masa tarczy 167 g = 0,167 kg masa tarczy 180 g = 0,18 kg
Numer pomiaru |
Czas 6 drgań [s] |
1 |
10,4 |
2 |
10,4 |
3 |
10,6 |
4 |
10,2 |
5 |
10,2 |
6 |
10,2 |
tśr |
10,33 |
Numer pomiaru |
Czas 6 drgań [s] |
1 |
10,2 |
2 |
10,0 |
3 |
10,2 |
4 |
10,0 |
5 |
10,0 |
6 |
10,0 |
tśr |
10,06 |
b) Drewniany prostopadłościan masa 120 g = 0,12 kg
wymiary 10,9 x 10,9 x 2,1 [cm]
Wahadło pierwsze Wahadło drugie
Numer pomiaru |
Czas 6 drgań [s] |
1 |
11,0 |
2 |
11,0 |
3 |
10,8 |
4 |
11,0 |
5 |
11,0 |
6 |
10,8 |
tśr |
10,93 |
Numer pomiaru |
Czas 6 drgań [s] |
1 |
11,4 |
2 |
11,4 |
3 |
11,4 |
4 |
11,4 |
5 |
11,4 |
6 |
11,4 |
tśr |
11,4 |
c) Metalowy walec masa 110 g = 0,11 kg
wymiary h = 34,7 mm r = 19,03 mm
Wahadło pierwsze Wahadło drugie
Numer pomiaru |
Czas 6 drgań [s] |
||
1 |
10,8 |
||
2 |
10,6 |
||
3 |
10,8 |
||
4 |
10,8 |
||
5 |
10,8 |
||
6 |
10,8 |
||
tśr |
10,76 |
||
Numer pomiaru |
Czas 6 drgań [s] |
||
1 |
11,0 |
||
2 |
10,8 |
||
3 |
10,8 |
||
4 |
11,0 |
||
5 |
11,0 |
||
6 |
10,8 |
||
tśr |
10,8 |
||
d) Metalowy walec masa 200 g = 0,2 kg
wymiary h = 15,35 mm r = 39,2 mm
Wahadło pierwsze Wahadło drugie
Numer pomiaru |
Czas 6 drgań [s] |
||
1 |
9,2 |
||
2 |
9,4 |
||
3 |
9,4 |
||
4 |
9,4 |
||
5 |
9,6 |
||
6 |
9,2 |
||
tśr |
9,36 |
||
Numer pomiaru |
Czas 6 drgań [s] |
||
1 |
9,6 |
||
2 |
9,6 |
||
3 |
9,6 |
||
4 |
9,4 |
||
5 |
9,6 |
||
6 |
9,6 |
||
tśr |
9,56 |
||
e) Metalowy walec masa 400 g = 0,4 kg
wymiary h = 29,05 mm r = 39,5 mm
Wahadło pierwsze Wahadło drugie
Numer pomiaru |
Czas 6 drgań [s] |
||
1 |
8,0 |
||
2 |
8,0 |
||
3 |
8,2 |
||
4 |
8,0 |
||
5 |
8,2 |
||
6 |
8,0 |
||
tśr |
8,06 |
||
Numer pomiaru |
Czas 6 drgań [s] |
||
1 |
8,6 |
||
2 |
8,4 |
||
3 |
8,4 |
||
4 |
8,4 |
||
5 |
8,4 |
||
6 |
8,4 |
||
tśr |
8,43 |
||
2.2.2. Wyniki:
a) Drewniany prostopadłościan
Wahadło pierwsze Wahadło drugie
![]()
= 0,167 kg ![]()
= 0,18 kg
m = 0,14 kg m = 0,14 kg
T1 = 1,03 T2 = 1,01
C1 = 15,34 C2 = 15,16
I1 = 0,00135![]()
I2 = 0,00145![]()
I = 0,000034![]()
I' = 0,000029![]()
b) Drewniany prostopadłościan
Wahadło pierwsze Wahadło drugie
![]()
= 0,167 kg ![]()
= 0,18 kg
m = 0,12 kg m = 0,12 kg
T1 = 1,14 T2 = 1,09
C1 = 15,34 C2 = 15,16
I1 = 0,00135![]()
I2 = 0,00145![]()
I = 0,00023![]()
I' = 0,0001![]()
c) Metalowy walec
Wahadło pierwsze Wahadło drugie
![]()
= 0,167 kg ![]()
= 0,18 kg
m = 0,11 kg m = 0,11 kg
T1 = 1,08 T2 = 1,08
C1 = 15,34 C2 = 15,16
I1 = 0,00135![]()
I2 = 0,00145![]()
I = 0,000023![]()
I' = 0,00021![]()
d) Metalowy walec
Wahadło pierwsze Wahadło drugie
![]()
= 0,167 kg ![]()
= 0,18 kg
m = 0,2 kg m = 0,2 kg
T1 = 0,96 T2 = 0,94
C1 = 15,34 C2 = 15,16
I1 = 0,00135![]()
I2 = 0,00145![]()
I = 0,000087![]()
I' = 0,000042![]()
e) Metalowy walec
Wahadło pierwsze Wahadło drugie
![]()
= 0,167 kg ![]()
= 0,18 kg
m = 0,4 kg m = 0,4 kg
T1 = 0,84 T2 = 0,81
C1 = 15,34 C2 = 15,16
I1 = 0,00135![]()
I2 = 0,00145![]()
I = 0,00035![]()
I' = 0,00021![]()
Obliczenie momentu bezwładności brył z wzorów:
Dla prostopadłościanu
![]()
gdzie
m - masa bryły
a, b - długość krawędzi podstawy
Dla walca![]()
![]()
gdzie
m - masa bryły
r - promień podstawy
a) Drewniany prostopadłościan masa 140 g = 0,14 kg
wymiary a x b = 0,08 x 0,08 [m]
I = 0,00082 ![]()
b) Drewniany prostopadłościan masa 120 g = 0,12 kg
wymiary a x b = 0,109 x 0,109 [m]
I = 0,00027 ![]()
c) Metalowy walec masa 110 g = 0,11 kg
wymiary r = 19,03 [mm] = 0,019 [m]
I = 0,000019 ![]()
d) Metalowy walec masa 200 g = 0,2 kg
wymiary r = 39,2 [mm] = 0,0392 [m]
I = 0,00015 ![]()
e) Metalowy walec masa 400 g = 0,4 kg
wymiary r = 39,5 [mm] = 0,0395 [m]
I = 0,00063 ![]()
3. WNIOSKI
wartość wyznaczonego przez nas momentu bezwładności bryły i przyspieszenia ziemskiego nie jest zbyt dokładna, ponieważ na wyniki pomiarów wpływ ma wiele czynników:
szerokość geograficzna, na której się znajdujemy,
brak uwzględnienia momentu bezwładności drucika i walca (modelującego u nas punkt materialny), a także oporu powietrza,
błąd pomiaru stopera,
niedokładność czynnika ludzkiego.
przeprowadzając pomiar czasu trwania dziesięciu okresów, zauważyliśmy że drgania naszej tarczy, podobnie jak w przypadku drgań wahadła matematycznego są drganiami tłumionymi. Jest to spowodowane różnymi oporami tarcia, z tego też powodu ich amplituda maleje z czasem do zera. Jednak okres tych drgań, jako że jest niezależny od amplitudy, nie ulega zmianie. Dlatego, aby wyznaczyć okres drgań T ,oraz aby wyznaczyć moment bezwładności dla brył pod uwagę bierzemy 1/10 czasu, która przypada na 10 badanych przez nas okresów(odpowiednio by wyznaczyć przyśpieszenie ziemskie przy pomocy wahadła bierzemy 1/10 czasu przypadającą na 10 badanych okresów). Robimy tak, ponieważ odstępy T pomimo zanikania amplitudy drgań są między sobą równe.
aby otrzymać okres drgań T musieliśmy uśrednić wyznaczone przez nas wartości czasu drgań tarczy t, a co za tym idzie otrzymana przez nas wartość jest średnią arytmetyczną podzieloną przez 10,
naszym zdaniem wartość uzyskana z wzoru tablicowego jest o wiele wiarygodniejsza, niż ta otrzymana z wzoru doświadczalnego, ponieważ nie było koniecznością uśrednianie jakichkolwiek wartości, wszystkie te które potrzebowaliśmy do wyznaczenia momentu
bezwładności były nam podane.
zaobserwowaliśmy również, że w doświadczeniu, w którym wyznaczaliśmy okres drgań dla brył sztywnych, kiedy kładliśmy na tarczę bryły o mniejszej masie czas 10 okresów był mniejszy (zatem T też był większy ). Natomiast w doświadczeniu z wahadłem matematycznym zauważyliśmy, że po skróceniu długości wahadła czas 10 wahnięć uległ zmniejszeniu (czyli im wahadło jest krótsze tym okres drgań jest mniejszy)
![]()
R0
O
B''
B'
B
C'
C
C''
O'
l
l-z
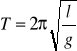
![]()
Wyszukiwarka
Podobne podstrony:
sprawozdanie termoogniwo, Dokumenty PWZS Zamość, Mechanika i Budowa maszyn I semestr
termoogniwo, Dokumenty PWZS Zamość, Mechanika i Budowa maszyn I semestr
inżynieria materiałowa Hejwowski, Dokumenty PWZS Zamość, Mechanika i Budowa maszyn I semestr
polarymetr 2, Dokumenty PWZS Zamość, Mechanika i Budowa maszyn I semestr
Model matematyczny podsystemu silnika -Bielski, Mechanika i budowa maszyn, Semestr IX, Praca przejsc
sprawozdanie z izolacyjności akustycznej ekranów, AGH WIMIR Mechanika i Budowa Maszyn, Rok III, I se
tech i sys pom - cw1 - sprawozdanie, Politechnika Lubelska (Mechanika i Budowa Maszyn), Semestr 3, T
MO - sprawozdanie 1, Politechnika Poznańska Mechanika i Budowa Maszyn, Semestr 1, LOM
tech i sys pom - cw2 - sprawozdanie, Politechnika Lubelska (Mechanika i Budowa Maszyn), Semestr 3, T
zaliczenie odpowiedzi, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Bud
Inspiracja utworem... - referat, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mecha
Siemens, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
polimery, Politechnika Lubelska (Mechanika i Budowa Maszyn), Semestr 1, Tworzywa polimerowe
zadania z egzaminu, Politechnika Poznańska - Wydział Budowy Maszyn i Zarządzania, Mechanika i Budowa
patenty1, Mechanika i budowa maszyn, Semestr VII, Ochrona patentowa
SYSTEM TOLL, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
GRUNDIG, Mechanika i budowa maszyn, Semestr VI, Informatyka w eksploatacji pojazdów, Prezentacja
więcej podobnych podstron