FINANSE - ĆWICZENIA

WARTOŚĆ PIENIĄDZA W CZASIE.

Kapitalizacja odsetek - naliczanie odsetek po okresie wyliczeniowym i dopisywanie ich do kapitału. W następnym okresie naliczamy odsetki od kwoty wyższej o naliczone odsetki.

Jeżeli występuje kapitalizacja, to mówimy o rachunku odsetek złożonych i im częściej występuje, tym lepiej, a jeżeli nie występuje, to mówimy o rachunku odsetek prostych.

Stopa procentowa - rozumiana jest w dwojaki sposób:

I - jest to wyliczona stopa procentowo cena za jaką dawca kapitału gotów jest na pewien czas zrezygnować ze swoich pieniędzy;

II - jest to wyrażona procentowo cena, jaką jest gotów zapłacić biorca kapitału
za dysponowanie przez pewien czas pożyczonym pieniądzem.

Wartość bieżąca mówi nam ile jest dla nas dzisiaj warta kwota pieniędzy,
którą mamy posiadać w przyszłości po określonej stopie dyskontowej.

STOPA DYSKONTOWA - jest to stopa procentowa stosowana w odniesieniu
do przyszłych płatności odzwierciedlająca poziom ryzyka oraz niepewność związana
z czynnikiem czasu.

ODSETKI W LATACH

O = K
p
n
0,81

O - odsetki

K - zainwestowany kapitał

p - stopa procentowa

n - czas w latach

0,81 - różnica od podatku 0,19 = 100%

ODSETKI W DNIACH

O =

0,81

t - czas w dniach

365 - liczba dni w roku

WZÓR NA WARTOŚĆ PRZYSZŁĄ W RACHUNKU ODSETEK PROSTYCH
(bez kapitalizacji).

FV = PV
( 1 + p
n )

FV - wartość przyszła

PV - wartość bieżąca

p - stopa procentowa

n - czas w latach

WZÓR NA WARTOŚĆ PRZYSZŁĄ PO UWZGLĘDNIENIU PODATKU.

FV' = ( FV - PV)
0,81 + PV

[ własna notatka:

( FV - PV) - wyliczenie odsetek ; wzór ten stosujemy w każdym przypadku, gdzie liczymy FV - oprócz lokaty jednodniowej ]

WZÓR NA WARTOŚĆ PRZYSZŁĄ PRZY ROCZNEJ KAPITALIZACJI ODSETEK

FV = PV
( 1 + p )

WZÓR NA WARTOŚĆ PRZYSZŁĄ , GDY KAPITALIZACJA WYSTĘPUJE CZĘŚCIEJ NIŻ RAZ W ROKU

FV = PV
( 1 +
) ^m
n

m - ilość kapitalizacji w ciągu roku

WZÓR NA WARTOŚĆ BIEŻĄCĄ PRZY NOCNEJ KAPITALIZACJI ODSETEK

PV = FV

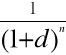
d - stopa dyskontowa

WZÓR NA WARTOŚĆ BIEŻĄCĄ, GDY KAPITALIZACJA WYSTĘPUJE CZĘŚCIEJ NIŻ RAZ W ROKU

PV = FV

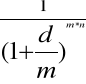
Zadanie 1

Oblicz ile będzie warta kwota 10 500zł ulokowana w banku na 3 lata, gdy bank zaoferuje nam oprocentowanie w wysokości 6% rocznie, a odsetki naliczone będą według rachunku odsetek prostych.

Korzystam ze wzoru na wartość przyszłą w rachunku odsetek prostych (bez kapitalizacji):

FV = PV
( 1 + p
n )

PV = 10 500zł

p = 6% = 0,06

n = 3 lata

FV = 10500 ( 1 + 0,06 * 3 )

FV = 12 390zł

FV' = ( FV - PV)
0,81 + PV

FV' = ( 12390 - 10500 ) * 0,81 + 10500

FV' = 12031zł

Zadanie 2

Załóżmy, że ulokowaliśmy 50 000zł na rachunku bankowym oprocentowanym 9% w skali roku przy rocznej kapitalizacji odsetek na 4 lata.

Oblicz, jaka będzie przyszła wartość tej kwoty po upływie 4 lat.

Korzystam ze wzoru na wartość przyszłą przy rocznej kapitalizacji odsetek:

FV = PV
( 1 + p )

FV = 50 000 * ( 1 + 0,09 ) ⁴

FV = 70 579zł

FV' = ( FV - PV)
0,81 + PV

FV' = ( 70 579 - 50 000 ) * 0,81 + 50 000

FV' = 66 669zł

Zadanie 3

Oblicz wysokość odsetek od lokaty jednodniowej założonej na kwotę 15 000zł oprocentowanej 4,85% w skali roku.

[ Stosujemy tutaj wzór na odsetki w dniach , ale bez podatku, gdyż jest to lokata jednodniowa, kwota odsetek nie przekracza 2,45zł]

O =

0,81

czyli O =

O =

O
1,99 zł

Zadanie 4

12 stycznia ubiegłego roku ulokowano w banku wkład w wysokości 10 000zł na okres jednego roku. Jednak 21 listopada tego samego roku zerwano lokatę. Regulamin lokat obowiązujący w tym banku przewiduje, że w takim przypadku odsetki naliczane są według zasad rachunku odsetek prostych wg stopy procentowej równej 3,5% w skali roku.

Oblicz wysokość należnych odsetek.

Liczba dni: od 12 stycznia2009r. do 21 listopada 2009r.

365 dni - 12 dni stycznia - 11 dni listopad - 31 dni grudzień = 313 dni trwała lokata

Korzystam ze wzoru na odsetki w dniach:

O =

0,81

O =

0,81 =243

Odp. : Kwota należnych odsetek wynosi 243 zł.

Zadanie 5

Kwota w wysokości 30 000 zł została ulokowana na rachunku bankowym oprocentowanym na 14% w skali roku na 5 lat.

Oblicz przyszłą wartość tej kwoty przy kapitalizacji półrocznej i kwartalnej.

Która z lokat jest korzystniejsza?

Korzystam: ze wzoru na wartość przyszłą , gdy kapitalizacja występuje częściej niż raz w roku

FV = PV
( 1 +
) ^m
n

m - ilość kapitalizacji w ciągu roku

Obliczam wartość przyszłą przy kapitalizacji półrocznej:

FV = 30000
( 1 +
) ^2
5

FV = 59 015

FV' = ( FV - PV)
0,81 + PV

FV' = ( 59015 - 30000)
0,81 + 30000

FV' = 53 502

Obliczam wartość przyszłą przy kapitalizacji kwartalnej:

FV = 30000
( 1 +
) ^4
5

FV = 59 693

FV' = ( FV - PV)
0,81 + PV

FV' = ( 59693 - 30000)
0,81 + 30000

FV' = 54 051

Odp.: Korzystniejsza jest lokata z kapitalizacją kwartalną.

Zadanie 6

Jaką kwotę musimy ulokować dziś na koncie bankowym przy stopie dyskontowej 15% i rocznej kapitalizacji odsetek, aby za 3 lata otrzymać 250 000zł.

Korzystam ze wzoru na wartość bieżącą przy nocnej kapitalizacji odsetek:

PV = FV

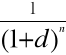
d - stopa dyskontowa

PV = 250000

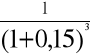
PV = 164 379

Odp.: Musimy ulokować kwotę w wysokości 164 379zł.

Zadanie 7

Jaką kwotę musimy ulokować dziś na koncie bankowym przy stopie dyskontowej 7%
i dwumiesięcznej kapitalizacji odsetek, aby za 5 lata otrzymać 100 000zł.

Korzystam ze wzoru na wartość bieżącą, gdy kapitalizacja występuje częściej niż raz w roku:

PV = FV

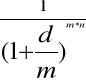
PV = 100000

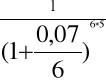
PV = 70 612

Odp.: Musimy ulokować kwotę w wysokości 70 612 zł.

Zadanie 8

Oblicz wartość lokaty w wysokości 70 tys. zł. oprocentowanej 9% przy kwartalnej kapitalizacji odsetek zakładając, że zostanie ona zlikwidowana za 2 lata.
Oceń czy korzystniejsze jest ulokowanie tej kwoty na ten sam okres w innym banku, który oferuje oprocentowanie 11%, lecz występuje kapitalizacja roczna.

Korzystam: ze wzoru na wartość przyszłą , gdy kapitalizacja występuje częściej niż raz w roku

FV = PV
( 1 +
) ^m
n

m - ilość kapitalizacji w ciągu roku

Obliczam wartość przyszłą przy kapitalizacji kwartalnej:

FV = 70000
( 1 +
) ^4
2

FV = 83 638

FV' = ( FV - PV)
0,81 + PV

FV' = ( 83638 - 70000)
0,81 + 70000

FV' = 81 047

Obliczam wartość przyszłą przy rocznej kapitalizacji odsetek:

FV = PV
( 1 + p )

FV = 70000
( 1 + 0,11 )

FV = 86 247

FV' = ( FV - PV)
0,81 + PV

FV' = ( 86247 - 70000)
0,81 + 70000

FV' = 83 160

Odp.: Korzystniejsza jest oferta na 11% z kapitalizacją roczną.

Zadanie 9

Oblicz kwotę odsetek od 6-cio miesięcznej lokaty, jeżeli:

1. lokata trwa przez pierwszą połowę roku,

2. kwota depozytu wynosi 6 tys. zł,

3. odsetki są naliczane według zmiennej stopy procentowej, w ciągu dwóch pierwszych miesięcy było to 16%, zaś w ciągu kolejnych czterech 14%,

4. obowiązuje miesięczna kapitalizacja odsetek .

Porównaj obliczone odsetki z sytuacją, gdyby naliczono je według stałej stopy 15,5%.

Stosujemy: Wzór na odsetki w dniach ( sześć razy, tyle ile trwa lokata).

O =

0,81

O Styczeń =

0,81

O Styczeń = 66

O Luty =

0,81

O Luty = 60

O Marzec =

0,81

O Marzec = 59

O Kwiecień =

0,81

O Kwiecień = 58

O Maj =

0,81

O Maj = 60

O Czerwiec =

0,81

O Czerwiec = 59

Odsetki za okres I-VI wg zmiennej stopy procentowej wynoszą:
6303+59 - 6000 = 362zł

Rok kalendarzowy dzielimy na:

I połowa - 181dni

II połowa - 184 dni.

Obliczamy odsetki wg stałej stopy:

O I-VI =

0,81

O I-VI = 374

Odp.: Korzystniejsza jest lokata założona na pół roku przy stałej stopie procentowej.

WZÓR NA WARTOŚĆ PRZYSZŁĄ PRZY ROCZNEJ KAPITALIZACJI ODSETEK I RÓŻNEJ STOPIE PROCENTOWEJ W POSZCZEGÓLNYCH OKRESACH

FV = PV ( 1 + p1 ) * ( 1 + p2 ) * ......... * ( 1 + pn )

WZÓR NA WARTOŚĆ PRZYSZŁĄ PRZY RÓŻNEJ STOPIE PROCENTOWEJ W POSZCZEGÓLNYCH OKRESACH I KAPITALIZACJI WYSTĘPUJĄCEJ CZĘŚCIEJ NIŻ RAZ W ROKU

FV = PV
*
* ......... *

m - ilość kapitalizacji w ciągu roku

Zadanie 10

Zamierzamy ulokować 37 tys. zł. na 3 lata w banku. Przewidywana stopa procentowa wynosi odpowiednio: 6% w pierwszym roku, 8% w drugim roku i 7% w trzecim.

Oblicz kwotę jaką otrzymamy po trzech latach.

Korzystam ze wzoru na wartość przyszłą przy rocznej kapitalizacji odsetek i różnej stopie procentowej w poszczególnych okresach:

FV = PV ( 1 + p1 ) * ( 1 + p2 ) * ......... * ( 1 + pn )

FV = 37000 ( 1 + 0,06 ) * ( 1+ 0,08 ) * ( 1+ 0,07 )

FV = 45323

FV' = ( FV - PV)
0,81 + PV ( - Wzór na wartość przyszłą po uwzględnieniu podatku. )

FV' = (45323 - 37000 ) * 0,81 + 37000

FV' = 43742

( 45323 - 43742 = 1581 zł podatek )

”””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””

Zadanie 11

Możemy ulokować 45 tys. na 4 lata.

Stopa procentowa będzie się kształtowała następująco:

- 6,5% w roku pierwszym z kapitalizacją półroczną;

- 6,9% w roku drugim z kapitalizacją kwartalną;

- 6,2% w roku trzecim z kapitalizacją roczną;

- 5,9% w roku czwartym z kapitalizacją dwumiesięczną.

Policzyć kwotę jaką otrzymamy po 4 latach.

Korzystam ze wzoru na wartość przyszłą przy różnej stopie procentowej w poszczególnych okresach i kapitalizacji występującej częściej niż raz w roku:

FV = PV
*
* ......... *

FV = 45000
*
*
*

FV = 45000 * 1,0661 * 1,0708 * 1,062 * 1,0605

FV = 57 857

FV' = ( FV - PV)
0,81 + PV ( - Wzór na wartość przyszłą po uwzględnieniu podatku. )

FV' = (57857 - 45000 ) * 0,81 + 45000

FV' = 55414

( 57857 - 55414 = 2443 zł podatek )

WZÓR NA WARTOŚĆ BIEŻĄCĄ PRZY ROCZNEJ KAPITALIZACJI ODSETEK
I RÓŻNEJ STOPIE DYSKONTOWEJ W POSZCZEGÓLNYCH OKRESACH:

PV = FV *
*
*........*

WZÓR NA WARTOŚĆ BIEŻĄCĄ PRZY RÓŻNEJ STOPIE DYSKONTOWEJ
W POSZCZEGÓLNYCH OKRESACH I KAPITALIZACJI WYSTĘPUJĄCEJ CZĘŚCIEJ NIŻ RAZ W ROKU

PV = FV *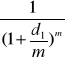
*
*........*

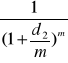
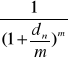
Zadanie 12

Pewne przedsięwzięcie przyniesie nam 170 tys. zł. Za 4 lata.

Oblicz ile musimy zainwestować w dniu dzisiejszym, jeśli stopa dyskonta wyniesie odpowiednio:

- dla I roku - 15%

- dla II roku - 16%

- dla III roku - 18%

- dla IV roku - 20%.

Wzór na wartość bieżącą przy rocznej kapitalizacji odsetek i różnej stopie dyskontowej w poszczególnych okresach:

PV = FV *
*
*
*

PV = 170000*
*
*
*

PV = 170000* 0,8696 * 0,8621 * 0,8475 * 0,8333

PV = 90 005

Odp.:
W dniu dzisiejszym musimy zainwestować 90 005 zł, aby w okresie 4 lat uzyskać 170tys.zł.

WZÓR NA EFEKTYWNĄ STOPĘ PROCENTOWĄ

- jest to stopa procentowa po uwzględnieniu kapitalizacji.

ESP =
_[%]

Zadanie 13

Mamy do ulokowania pewną kwotę pieniędzy na rok. Bank zaoferował nam oprocentowanie w wysokości 15% w ciągu roku z kwartalną kapitalizacją odsetek.

Powiedz, o ile procent przyrośnie nasz kapitał procentowy po upływie jednego roku.

ESP =
_[%]

ESP =
_[%]

ESP = 15,87 [%]

Odp.: Nasz kapitał przyrośnie o 15,87%

”””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””

RENTY - tj. ciąg płatności ( wpłaty lub wypłaty) o różnej lub tej samej wysokości dokonywane w równych odstępach czasu.

Płatności rent nazywane są ratami, a odstęp pomiędzy dwoma najbliższymi ratami nazywa się okresem bazowym.

Jeżeli renta ma skończoność ilość wpłat, to mówimy o rencie pewnej lub czasowej.

Jeżeli liczba rat jest nieskończona, to mówimy o rencie wieczystej.

Jeżeli wpłaty dokonywane są na początku okresu, to mówimy o rencie płatnej z góry
( z wyprzedzeniem).

Jeżeli wpłaty na koniec okresu, to mówimy o rencie płatnej z dołu ( bez wyprzedzenia).

Jeżeli wpłaty rat pokrywają się z okresem kapitalizacji, to mówimy o rencie zgodnej, inaczej prostej, a jeżeli się nie pokrywają, to mówimy o rencie niezgodnej, inaczej uogólnionej.

WZÓR NA WARTOŚĆ PRZYSZŁĄ RENTY PROSTEJ PRZY ROCZNEJ KAPITALIZACJI ODSETEK

- z góry: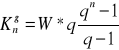

Założenie: q ≠1 ; q=1+p

K - wartość przyszła renty

n - czas w latach

W - raty wpłaty jednakowej wysokości

q=1+p ; gdzie p- nominalna stopa procentowa

- z dołu:

WZÓR NA WARTOŚĆ PRZYSZŁĄ RENTY PROSTEJ PRZY ŚRÓDROCZNEJ KAPITALIZACJI ODSETEK

- z góry:

Założenie: q ≠1 ; q=1+

_{m - ilość kapitalizacji w ciągu roku}

- z dołu:

Założenie: q ≠1 ; q=1+

P - stopa procentowa nominalna

WZÓR NA WARTOŚĆ RENTĘ NIEZGODNĄ (UOGÓLNIONĄ)

- występuje wtedy, gdy okresy wpłat nie zgadzają się z okresem kapitalizacji.

Mamy dwa warianty, gdy:

1. wpłaty są częstsze niż kapitalizacja;

2. kapitalizacja występuje częściej niż wpłaty.

Ad. 1

Wariant, gdy wpłaty są częstsze niż kapitalizacja:

- z góry:

Założenie: q ≠1 ; q=1+p

_{k - ilość wpłat w ciągu jednego okresu kapitalizacji}

- z dołu: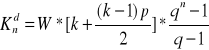

Założenie: q ≠1 ; q=1+p

Zadanie 14

Wyznaczyć przyszłą wartość renty po 3 latach i przy rocznej kapitalizacji odsetek, jeśli wysokość raty wynosi 200zł, a płatności są wnoszone:

1. na końcu każdego roku;

2. na początku każdego roku.

Nominalna stopa procentowa wynosi 3%.

Korzystam ze wzoru na wartość przyszłą renty prostej przy rocznej kapitalizacji odsetek:

- z góry: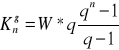

Założenie: q ≠1 ; q=1+p

K - wartość przyszła renty

n - czas w latach

W - raty wpłaty jednakowej wysokości

q=1+p ; gdzie p- nominalna stopa procentowa

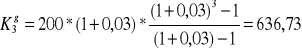
- z dołu: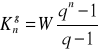

Zadanie 15

Wyznaczyć przyszłą wartość renty z dołu i z góry po 2 latach przy kwartalnych wpłatach
i kwartalnej kapitalizacji odsetek. Rata renty wynosi 500zł, a nominalna stopa procentowa wynosi 3,2%.

Korzystam ze wzoru na wartość przyszłą renty prostej przy śródrocznej kapitalizacji odsetek:

- z góry:

Założenie: q ≠1 ; q=1+

_{m - ilość kapitalizacji w ciągu roku}

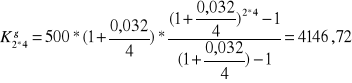
- z dołu:

Założenie: q ≠1 ; q=1+

P - stopa procentowa nominalna

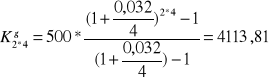
Zadanie 16

Załóżmy, że na książeczkę mieszkaniową przez 10 lat wpłacano miesięcznie 250zł przy nominalnej stopie procentowej równej 4% i rocznej kapitalizacji odsetek. Należy ustalić końcową wartości zgromadzonego funduszu, jeśli wpłaty były dokonywane:

a. na początku każdego miesiąca,

b. na końcu każdego miesiąca.

Rozwiązanie: Renta niezgodna, gdy wpłaty są częstsze niż kapitalizacja.

- z góry:

Założenie: q ≠1 ; q=1+p

_{k - ilość wpłat w ciągu jednego okresu kapitalizacji}

- z dołu:

Założenie: q ≠1 ; q=1+p

Zadanie 17

Przez dwa lata wpłacano kwartalnie 500zł. Nominalna stopa procentowa wynosi 6% przy rocznej kapitalizacji odsetek. Policz końcową wartość zgromadzonego kapitału, jeśli wpłat dokonywano:

a. na początku każdego miesiąca,

b. na końcu każdego miesiąca.

Rozwiązanie: Renta niezgodna, gdy wpłaty są częstsze niż kapitalizacja.

- z góry:

Założenie: q ≠1 ; q=1+p

_{k - ilość wpłat w ciągu jednego okresu kapitalizacji}

- z dołu:

Założenie: q ≠1 ; q=1+p

Zadanie 18

Wyznacz cenę samochodu na koniec roku, jeśli biorący udział w transakcji uzgodnili, że należność będzie spłacana w 12-tu jednakowych miesięcznych ratach z wyprzedzeniem po pół tysiąca każda (500zł). Nominalna stopa procentowa wynosi 3% przy rocznej kapitalizacji odsetek.

Rozwiązanie: RENTA NIEZGODNA → z góry.

- z góry:

Założenie: q ≠1 ; q=1+p

_{k - ilość wpłat w ciągu jednego okresu kapitalizacji}

”””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””

RENTA UOGÓLNIONA - kapitalizacja występuje częściej niż wpłaty

- z góry: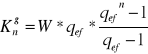

Założenie:
;

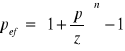
_{p - stopa procentowa dla przyjętego okresu wpłat}

_{- efektywna stopa procentowa dla przyjętego okresu wpłat}

_{z - ilość kapitalizacji w jednym okresie wpłat}

_{n - ilość wszystkich wpłat kapitalizacji}

_{W - wysokość wpłaty równej wielkości}

- z dołu: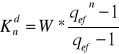

Zadanie 19

Na koniec każdego półrocza wpłacano do banku kwotę 500zł. Nominalna stopa procentowa wynosi 8%, a kapitalizacja odsetek jest kwartalna.

Należy wyznaczyć przyszłą wartość renty pod koniec 4 roku.

- z dołu: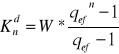

p= 4% stopa procentowa zgodna z przyjętym okresem wpłat mamy 8% na rok, wiec na półrocze wynosi 4%

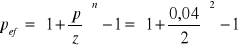
= 0,0404

= 1,0404

Zadanie 20

Na początku każdego kwartału wpłacano do banku 300zł. Nominalna stopa procentowa wynosi 12%, a kapitalizacja odsetek jest miesięczna.

Oblicz wartość końcowa kapitału na koniec 3 roku.

- z góry: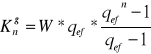

p= 12% dzielimy na 4 kwartały = 3%

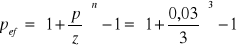
= 0,0303

= 1,0303

n= 3 lata mnożymy przez 4 kwartały w roku, co daje nam 12

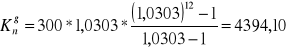
Zadanie 21

Bank ufundował roczne stypendium w kwocie 300zł miesięcznie płatne pod koniec każdego miesiąca.

Oblicz przyszłą wartość tego stypendium przy nominalnej stopie procentowej równej 3% i miesięcznej kapitalizacji odsetek.

Rozwiązanie:

RENTA ZGODNA , ŚRÓDROCZNA KAPITALIZACJA

- z dołu:
Założenie: q ≠1 ; q=1+

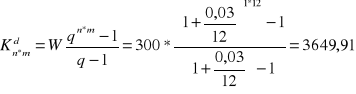
Zadanie 22

Miesięczna stopa procentowa wynosi 0,5%. Co dwa miesiące wpłacamy stałą kwotę 150 zł.

Oblicz wielkość zgromadzonego na koniec roku kapitału, jeśli wpłat dokonujemy z dołu przy rocznej kapitalizacji odsetek.

Renta niezgodna, gdy wpłaty są częstsze niż kapitalizacja.

- z dołu:

Założenie: q ≠1 ; q=1+p

”””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””””

22

---