Wykład VII. Gaz elektronów Fermiego.

W rozdziale tym zajmować się będziemy swobodnymi elektronami istniejącymi w ciałach stałych. Będą to na ogół metale. Do opisu własności elektronów w metalu posłużymy się prostym modelem w którym zakłada się co następuje:

1. Elektrony mogą się swobodnie poruszać wewnątrz próbki

2. Elektrony nie mogą opuścić metalu.

3. Elektrony nie oddziaływają pomiędzy sobą

W tej sytuacji ruch każdego elektronu można rozpatrywać niezależnie od pozostałych. Zagadnienie analizować będziemy używając mechaniki kwantowej. W tym formalizmie dozwolone energie pojedynczego elektronu oraz odpowiadające im funkcje falowe można otrzymać rozwiązując niezależne od czasu równanie Schrödingera

(VII-1)

gdzie
jest funkcją falową ,
energią potencjalną elektronu,
jest operatorem energii kinetycznej elektronu,
jest wartością własną energii. Zgodnie z naszymi początkowymi założeniami możemy przyjąć ,że potencjał
jest równy zero wewnątrz metalu oraz nieskończoność na zewnątrz . Dla uproszenia rozważań można przyjąć , że mamy do czynienia z sześcianem o boku L . Wówczas

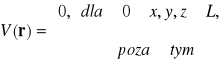
(VII-2)

Ponieważ elektrony nie mogą istnieć na zewnątrz metalu równanie (VII-1) ma sens tylko wewnątrz metalu gdzie przyjmuje następującą postać:

(VII-3)

Operator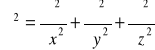
. Widać, że równanie (VII-3) ma rozwiązanie w postaci fali płaskiej

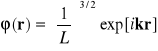
(VII-4)

gdzie stały czynnik przed eksponentem wynika z warunku normalizacji funkcji falowej :

(VII-5)

Po podstawieniu funkcji (VII-4) do równania (VII-3) i wykonaniu różniczkowania otrzymujemy następującą zależność energii od wektora falowego:

(VII-6)

gdzie

są odpowiednimi składowymi wektora falowego. Warto przypomnieć w tym miejscu związek pomiędzy wektorem falowym a pędem cząstki

(VII-7)

Wstawiając go do wzoru (VII-6) otrzymujemy klasyczną (znaną z klasycznej mechaniki) zależność energii kinetycznej cząstki swobodnej od pędu.

(VII-8)

Przedstawienie energii kinetycznej cząstki w postaci jej zależności od wektora falowego ( relacja VII-6) lub od pędu ( relacja VII-8) jest znacznie bardziej uniwersalne niż przedstawienie jej w funkcji prędkości
. Po pierwsze mamy tu do czynienia z dwoma wielkościami fizycznymi, wobec których obowiązują zasady zachowania (nie ma zaś zasady zachowania prędkości). Po drugie przedstawienie w funkcji wektora falowego może być użyte w jednolitej formie zarówno dla cząstek posiadających masę jak i dla cząstek o zerowej lub bliżej nieokreślonej masie (fotony, fonony). W następnych wykładach zostanie pokazane, że nośniki prądu w krysztale mogą nie mieć stałej masy.

Powróćmy do rozwiązań równania (VII-3). Z faktu, że elektrony nie mogą istnieć poza kryształem wynika, że funkcja falowa musi znikać na brzegu kryształu i poza kryształem. Sprowadza się to do warunku
dla x,y i z równych 0 i L. Funkcja w postaci (VII-4) spełnia ten warunek jeśli

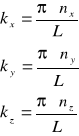
(VII-9)

gdzie
liczbami całkowitymi a L jest bokiem naszego sześcianu.

W przypadku jednowymiarowym funkcje falowe kilku najniższych stanów przedstawione są na rysunku (VII-1)

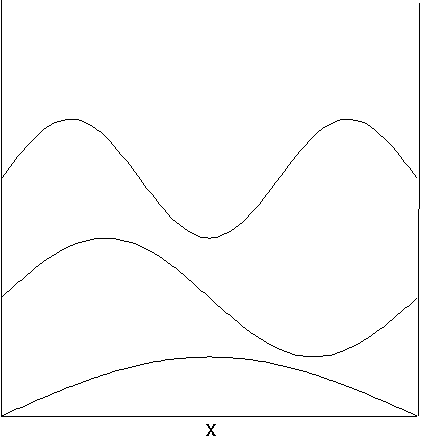
0 L

Mamy tu do pewnego stopnia sytuację analogiczną jak w przypadku fononów. Wynika to z takich samych warunków kwantyzacji nałożonych na elektronową funkcję falową jakie w przypadku fononów zostały nałożone na falę mechaniczną.

Druga analogia dotyczy kształtu potencjału. Łatwo zauważyć, że dla gazu elektronów swobodnych w metalu otrzymujemy dyskretne wartości energii, które są identyczne jak te otrzymane dla cząstki znajdującej się w trójwymiarowej studni potencjału o nieskończenie wysokich ścianach. Różnica polega na tym, że studnia potencjału miała zazwyczaj małe rozmiary, co powodowało że różnice energii pomiędzy poszczególnymi stanami były stosunkowo duże. Obecnie zaś mamy do czynienia z dużymi rozmiarami kryształu co powoduje, że stany energetyczne leżą bardzo blisko siebie. Stany a takim potencjale analizuje się nieco inaczej niż stany cząstki w studni potencjału. Zamiast obliczać poszczególne energie wygodnie się zapytać ile stanów energetycznych znajduje się w przedziale energii pomiędzy energią E i E+dE. Wielkość tą nazywamy energetyczną gęstością stanów. Spotkaliśmy się już z nią przy okazji analizy ciepła właściwego fononów.

Wracając do analogii z fononami. Podobnie jak i w tamtym przypadku zamiast rozważać skończony kryształ można określić stany własne układu zakładając periodyczność funkcji falowej z okresem L. Wówczas warunek periodyczności :

(VII-10)

prowadzi do następujących warunków określających dozwolone wartości wektora falowego :

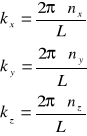
(VII-11)

Interesujące jest to, że warunki (VII-9) i (VII-11) są sobie równoważne. Wynika to z faktu ,że zawsze możemy wybrać dowolną wartość boku L naszego podstawowego sześcianu. W dalszym ciągu będziemy się posługiwali warunkiem (VII-11). Widać, że niezależnie od wartości wektora falowego jeden stan przypada na objętość
w przestrzeni pędów. Wobec powyższego gęstość stanów w przestrzeni pędów jest równa

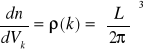
(VII-12)

Aby obliczyć energetyczną gęstość stanów postępujemy podobnie jak w przypadku gęstości stanów fononowych . Odpowiednie równanie będzie miało teraz postać:

(VII-13)

Identycznie jak w przypadku fononów
jest objętością w przestrzeni pędów, w której energia ( tym razem elektronu) ma stałą wartość. Zauważamy, że ponieważ zależność energii od wektora falowego określona jest wzorem (VII-6) energia będzie stałą na powierzchni kuli . Identycznie jak w przypadku fononów

. (VII-14)

Podstawiając (VII-14) do (VII-13) otrzymujemy

(VII-15)

Z relacji dyspersyjnej (VII-6) otrzymujemy
i stąd

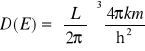
(VII-16)

Korzystając dalej z zależności (VII-6) otrzymamy ostatecznie:

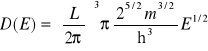
(VII-17).

W odróżnieniu od fononów elektrony, jako cząstki posiadające spin połówkowy są fermionami. Oznacza to, że stosuje się do nich zakaz Pauliego oraz podlegają statystyce Fermiego Diracka. Z zakazu Pauliego wynika, że w jednym stanie mogą znajdować się co najwyżej dwa elektrony różniące się spinem ( jeden ma spin równy
a drugi
) . Oznacza to, że jeśli w metalu znajduje się wiele elektronów to zajmować one będą kolejne stany energetyczne o coraz wyższej energii. W temperaturze 0K najwyższy obsadzony stan ma energię równa energii Fermiego.

Statystyka Fermiego.

Prawdopodobieństwo , że elektron znajduje się w stanie o energii E dane jest wzorem:

(VII-18).

Energia
zwana jest potencjałem chemicznym i jest zdefiniowana jako energia stanu, którego prawdopodobieństwo obsadzenia jest równe 0.5. Energia ta zależy od temperatury . W temperaturze 0K energia potencjału chemicznego jest z definicji równa energii poziomu Fermiego. To powoduje, że często zamiast potencjału chemicznego używamy terminu energii Fermiego
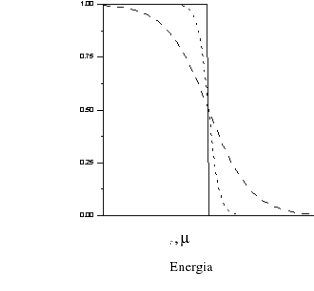
. Tak zdefiniowana energia Fermiego będzie zależała od temperatury. Wykres funkcji Fermiego przedstawiony jest na rysunku (VII-2)

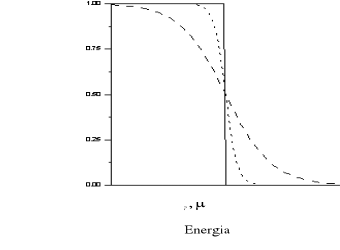
W zerowej temperaturze Funkcja (VII-18) ma postać schodkową:

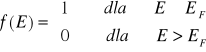
(VII-19)

Spróbujmy obliczyć energię Fermiego i potencjał chemiczny dla metalu, w którym w jednostce objętości znajduje się N elektronów. Można to zrobić korzystając z równości :

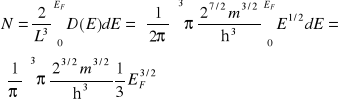
(VII-20)

We wzorze (VII-20) dodatkowy czynnik 2 pojawił się ze względu na to, że w jednym stanie znajdują się dwa elektrony. Ze wzoru (VII-20) wynika następujący wzór na energię Fermiego

(VII-21)

Wielkość
nosi nazwę wektora Fermiego.

Potencjał chemiczny
może być obliczony z równości :

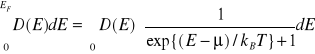
(VII-22)

Dla niskich temperatur równanie to ma przybliżone rozwiązanie w postaci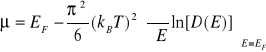
(VII-22a)

Zwróćmy raz jeszcze uwagę na konsekwencje faktu, że elektrony są fermionami. Wynika z tego ,że nawet w temperaturze 0K gaz elektronów swobodnych posiada określoną energię. Można zapytać jakiego rodzaju jest to energia i jakie są konsekwencje faktu , że nie jest ona równa energii stanu podstawowego.

Po pierwsze zauważmy, że stanom o wyższej energii odpowiada większy wektor falowy. W temperaturze zera bezwzględnego obsadzone są wszystkie stany leżące wewnątrz kuli o promieniu
- wektora Fermiego. Czasami nazywa się to kulą Fermiego. Wektor falowy funkcji falowej elektronu jest związany z prędkością fazową fali elektronu,
. Prędkość pojedynczego elektronu jest prędkością grupową fali elektronu, i wynosi
. Pomimo, że energia pojedynczego elektronu w krysztale liczona względem dna pasma przewodnictwa jest energią kinetyczną energia elektronu w gazie elektronowym, wynikająca z istnienia zakazu Pauliego, ma charakter energii potencjalnej. Dlatego mówimy o potencjale Fermiego i potencjale chemicznym.

Potencjał Fermiego może być wyznaczony jeśli znana jest praca wyjścia elektronów z metalu . Sytuacja przedstawiona jest na rysunku. VII-3 .

Rys VII- 3 schemat pasm energetycznych w metalu . Stany obsadzone przez elektrony zaznaczono przez cieniowanie.

E

Pasmo energetyczne częściowo

zapełnione

pasmo całkowicie zapełnione

Materiał próżnia

Praca wyjścia
określana jest jako różnica energii pomiędzy energią elektronu na zewnątrz materiału (w próżni) a energią Fermiego.

Znaczenie potencjału Fermiego widać jeśli zetkniemy ze sobą dwa materiały o różnej wartości energii Fermiego. Elektrony znajdujące się w materiale o wyższym poziomie Fermiego mają większą energię potencjalną niż elektrony w materiale o niższej energii Fermiego. Zetkniecie obu materiałów powoduje więc ruch elektronów, który ustanie dopiero po wyrównaniu się poziomów Fermiego w obu materiałach. Kiedy to nastąpi elektrycznie obojętne przed zetknięciem materiały ulegną po zetknięciu polaryzacji. Materiał, z którego odeszły elektrony będzie miał ładunek dodatni , a materiał do którego przeniknęły elektrony będzie miał ładunek ujemny. Sytuacja przedstawiona jest na rysunku (VII-4). Taki przepływ elektronów dążących do wyrównania potencjałów chemicznych odpowiedzialny jest za powstanie napięcia kontaktowego oraz zjawiska termoelektrycznego w metalach, a także nieliniowych efektów w złączach półprzewodnikowych.

Rys VII-4 Poziom Fermiego w złączy dwóch metali. Grubą strzałką oznaczono kierunek przepływu elektronów. Z rysunku widać, że ważna jest energia Fermiego liczona względem poziomu próżni.

Poziom próżni

Poziom Fermiego po

Zetknięciu materiałów

Materiał I Materiał II

Ciepło właściwe elektronów

Elektronowe ciepło właściwe definiujemy w ten sam sposób jak ciepło właściwe związane z istnieniem fononów. Tak jak w przypadku fononów obowiązuje relacja:

(VII-23)

Gdzie U jest całkowitą energią wewnętrzną układu , którą liczy się sumując energie wszystkich elektronów swobodnych istniejących w metalu. Podobnie jak dla fononów całkowitą energię otrzymuje się ze wzoru:

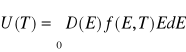
(VII_24).

gdzie D jest gęstością stanów , f, funkcją rozkładu Fermiego, E energią elektronu. W celu uproszczenia obliczeń wykorzystuje się następującą zależność :

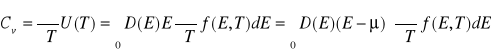
(VII-25)

Wzór powyższy jest prawdziwy ponieważ ilość elektronów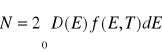
, nie zależy od temperatury. Stąd:

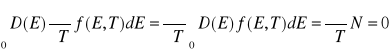
(VII-26)

Jeżeli mamy stosunkowo niską temperaturę to pochodna funkcji Fermiego jest różna od zera w niewielkim zakresie energii w pobliżu energii Fermiego. Wówczas całkowanie we wzorze (VII-25) można znacznie uprościć przyjmując, że w obszarze gdzie
mamy do czynienia ze stałą gęstością stanów . Zakładając, że
dostajemy

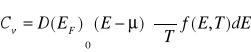
(VII-27)

Korzystając dalej ze wzoru ( VII-19) otrzymujemy

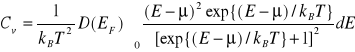
(VII-28)

Całkowanie we wzorze (VII-28) może być wykonane po zamianie zmiennych . Wprowadzając nową zmienną
otrzymujemy

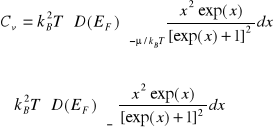
(VII-29)

Całkę we wzorze (VII-29) można policzyć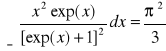
. Stąd ostatecznie

(VII-30)

Jeśli skorzystamy z zależności energii Fermiego od ilości elektronów N otrzymamy

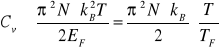
(VII-31)

Wprowadzono tu pojęcie temperatury Fermiego,
. Ze względu na fakt, że w metalu energia Fermiego jest znaczna temperatura Fermiego jest wynosi kilka tysięcy Kelwinów. To powoduje ,że przybliżony wzór (VII-31) jest słuszny również w temperaturach zbliżonych do temperatury pokojowej.

Możemy obecnie dokonać porównania wartości elektronowego i fononowego ciepła właściwego dla metalu. Przypomnijmy w tym celu wzór na fononowe ciepło właściwe w wysokich temperaturach (V-47)

(VII-32)

gdzie N_a jest równe ilości atomów w jednostce objętości . W wzorze (VII-31 ) N było równe gęstości elektronów swobodnych. Ponieważ w metalach mamy na ogół jeden elektron swobodny przypadający na jeden atom sieci liczby te są takie same. Pozostałe własności są stałymi liczbowymi. Widać, że pokojowej temperaturze dominuje fononowe ciepło właściwe. Inaczej może być w temperaturach wysokich, gdzie obie wielkości mają porównywalne wartości.

Przewodnictwo elektryczne metali

Model Drude'go

Aby otrzymać zależność prądu płynącego przez przewodnik od przyłożonego napięcia rozważmy materiał , w którym mamy „N” swobodnych nośników prądu w jednostce objętości. Załóżmy dalej ,że elektrony zderzają się ze sobą oraz z fononami i defektami sieci, oraz że średni czas pomiędzy dwoma zderzeniami wynosi
. Pod wpływem zewnętrznego pola elektrycznego o natężeniu
elektrony ulegają przyspieszeniu i w czasie pomiędzy kolejnymi zderzeniami uzyskują dodatkową prędkość w kierunku pola
, zwaną prędkością unoszenia. Odpowiednie równanie ruchu elektronów przyjmuje postać

(VII-33)

gdzie e jest ładunkiem a m masą elektronu. Zgodnie ze znaną definicją gęstość prądu daje się obliczyć ze wzoru:

(VII-34)

gdzie wielkość
nazywana jest ruchliwością elektronów. Ostatecznie otrzymuje się następujący wzór na przewodnictwo elektryczne metalu :

(VII-35)

Jeśli weźmie się pod uwagę kwantowy model gazu elektronów swobodnych to zauważymy od razu, że nie wszystkie elektrony mogą brać udział w przewodnictwie. W szczególności do przewodnictwa nie mogą przyczyniać się elektrony znajdujące się w stanach o energiach mniejszych niż energia Fermiego. Faktycznie w przewodnictwie biorą udział tylko elektrony o energii równej energii Fermiego, tylko one bowiem mogą zmienić swoją energię przechodząc do wyższych nie obsadzonych stanów energetycznych. Elektrony o energiach mniejszych niż energia Fermiego nie ulegają przyspieszeniu pod wpływem zewnętrznego pola elektrycznego ponieważ stany o wyższych energiach, do których powinny przejść po uzyskaniu dodatkowej prędkości unoszenia są już obsadzone. Wydawałoby się, że N we wzorach (VII-33) - (VII-35) nie jest całkowitą ilością elektronów a tylko ilością elektronów mających energię Fermiego. Z drugiej jednak strony, jak zostanie pokazane w następnym paragrafie, kwantowy model gazu elektronów swobodnych Fermiegio daje taką samą zależność przewodnictwa od gęstości elektronów w metalu jak klasyczny model Drude'go.

Kwantowy model przewodnictwa elektrycznego

Aby otrzymać odpowiednie wyrażenie na przewodnictwo elektronowe w modelu kwantowym rozważmy przewodnik o stałym przekroju S, przedstawiony na Rysunku VII-5

Gęstość prądu będzie równa ilości elektronów przechodzących przez powierzchnie S. Podobnie jak w przypadku transportu ciepła ilość ta będzie równa różnicy pomiędzy ilością elektronów przechodzących w jednostce czasu z lewej na prawą i prawej na lewą. Rozważmy elektrony mające pęd k. Przyczynek do gęstości prądu pochodzący od tych elektronów będzie równy ;

(VII-36)

we wzorze (VII-36) wykorzystano fakt , że liczba elektronów o pędzie k jest dana przez iloczyn gęstości stanów w przestrzeni pędów i funkcji rozkładu Fermiego :

jest prędkością elektronu w kierunku x

Z zasady zachowania pędu otrzymujemy
, zaś związek dyspersyjny dla elektronów daje nam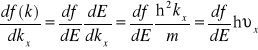
. Wstawiając obydwie te zależności do wzoru (VII-35) otrzymujemy:

(VII-37)

Aby otrzymać całkowitą gęstość prądu należy dokonać sumowania po wszystkich elektronach mających dowolne pędy. Sprowadza się to do całkowania po wszystkich możliwych pędach:

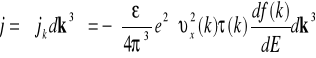
(VII-38)

Całkowanie odbywa się po objętości w przestrzeni pędów. Możemy wybrać wygodną dla nas objętość, w której energia elektronów ma wartość stał
. Zastępując dalej całkowanie po wektorach falowych dk całkowaniem po energii dE oraz korzystając z faktu, że
, gdzie
, gdzie jest bezwzględną wartością prędkości elektronu i
otrzymujemy

(VII-39)

Dla niskich temperatur, gdy
można skorzystać z przybliżonego wzoru

, (VII-40)

gdzie
jest funkcją delta Diracka . Otrzymujemy wówczas

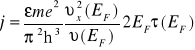
(VII-41)

Korzystając dalej z następujących zależności
,
i
otrzymujemy

(VII-42)

Ostatecznie otrzymujemy następujący wzór określający przewodnictwo metali

(VII-43)

oraz ruchliwość elektronów

(VII-44)

Granice zastosowania modelu gazu elektronów swobodnych.

Porównując model gazu Fermiego z realnymi elektronami w metalu zauważamy, że główne uproszczenie teorii polega na zaniedbaniu potencjału krystalicznego. Jak wiadomo konsekwencją istnienia periodycznego potencjału krystalicznego jest istnienie w przestrzeni pędów struktury periodycznej zwanej siecią odwrotną. Jeśli rozważa się dynamikę cząstek pojawia się konieczność uwzględnienia istnienia pierwszej strefy Brillouina i faktu, że nie może istnieć cząstka, której fala materii ma wektor falowy większy niż promień tej strefy. Koncentrując się na elektronach w metalu, widzimy że jeśli wektor Fermiego jest mały w porównaniu rozmiarami strefy Brillouina to istnienie granicy strefy nie wpływa w żaden sposób na dynamikę elektronów, jeśli zaś wektor Fermiego jest porównywalny lub większy od promienia strefy wówczas teoria gazu elektronów Fermiego może być nieprawdziwa. Należy wówczas uwzględnić istnienie struktury periodycznej kryształu Przypomnijmy, wektor Fermiego jest dany przez:

(VII-45)

gdzie n jest ilością elektronów walencyjnych w metalu a V jego objętością . Zakładając, że mamy jeden elektron na jeden atom i jeden atom na jedną komórkę elementarną, oraz że stała sieci równa się
otrzymamy:
i
. Promień pierwszej strefy Brillouina jest w tym przypadku równy
. Jak widać obie te wielkości są porównywalne.

11

1

Rys VI-1.Funkcje falowe trzech stanów o najniższej energii

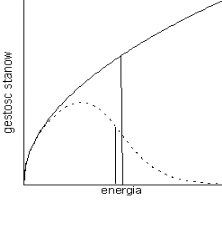
Fig .VI-2 a) funkcja rozkładu Fermiego, Linia ciągła odpowiada temperaturze 0K, krzywe przerywane odpowiadają temperaturom 0.1 i 0. 25

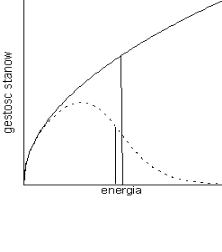
b) funkcja obsadzenia stanów trójwymiarowego gazu Fermiego dla temperatury 0K i 0.25
. Na rysunku zaznaczono również gęstość stanów. Widać, że potencjał chemiczny dla temperatury wyższej niż 0K ma wartość mniejszą niż E_F

a

b

Energia

E_F poziom Fermiego

Energia

N(k-dk_x)

N(k-dk_x)-N(k)

S N(k)

---